决策树(Decision Tree)是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶子节点代表一种类别。它是一种十分常用的分类方法,并且是一种监督学习(就是给定一些样本,每个样本都有一组属性和一个类别,这些类别是事先确定好的,通过学习得到一个分类器,当出现新的对象时,分类器能给出正确的分类。)
我们在使用决策树进行决策的过程中,先是从根节点开始,判断要分类项中的对应的特征属性,根据判断结果选择输出分支,直到到达叶子节点,决策完成。
决策树有如下表示形式:
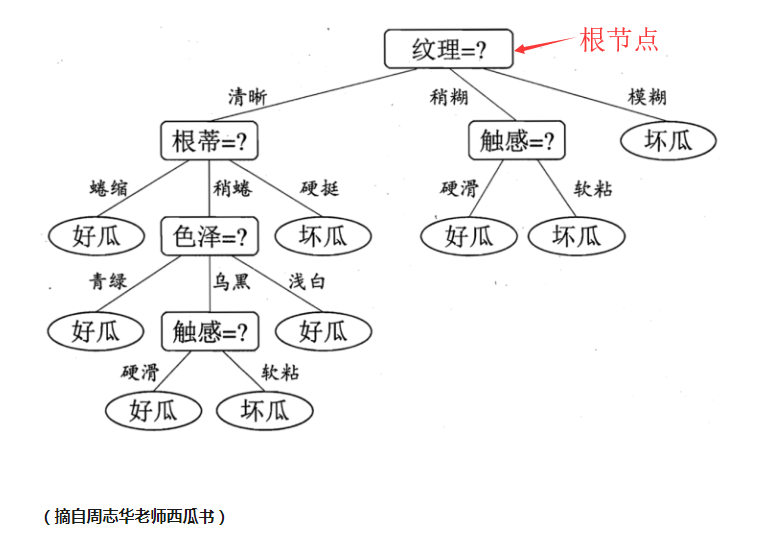
举例
现在有一个西瓜,它的特点是纹理清晰、根蒂硬挺,判断一下它是好瓜或坏瓜。步骤如下:
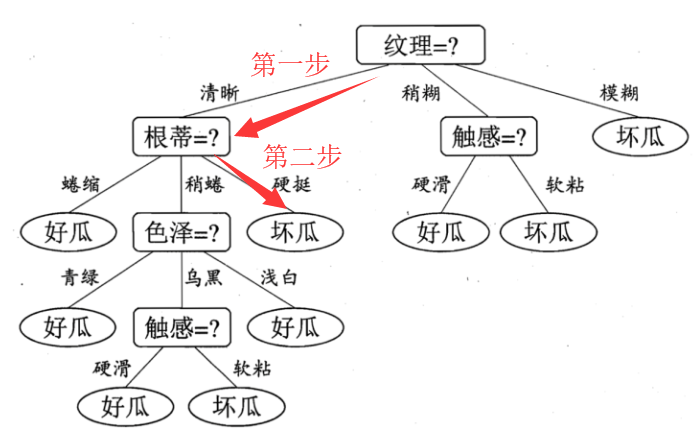

关键点
决策树的判断过程相当于树从根节点到某一个叶子节点的遍历。下一步怎么走是由特征的具体特征属性决定。因此决策树的关键就是创建决策树,有了树,就可以进行遍历操作。而创建决策树的关键是选择最优划分属性。
ID3算法
先介绍几个概念
信息熵:是度量样本集合复杂度(不确定度)的最常用的指标,定义如下

信息增益:信息熵-条件熵。
在ID3算法中,采用信息增益这个量来作为划分属性的标准。我们选取使得信息增益最大的特征进行分裂!如果选择一个特征后,它的信息增益最大,就选取这个特征。
举例
现有如下数据
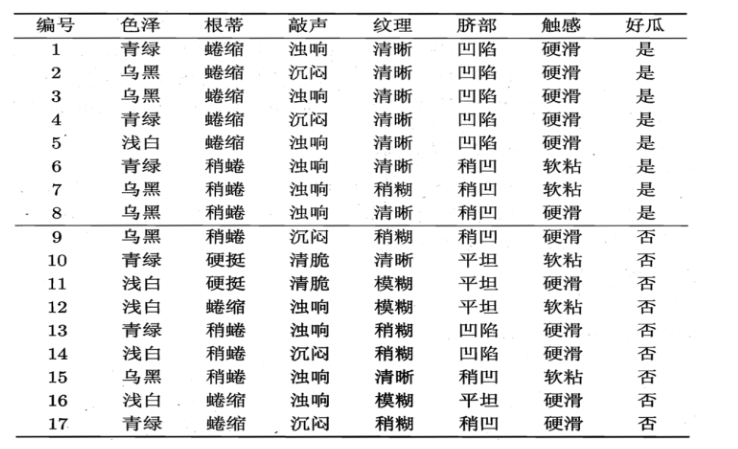
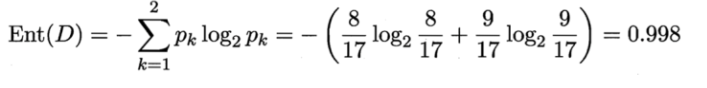
就拿色泽来说,可能取值:{青绿、乌黑、浅白}
D1(色泽=青绿) = {1, 4, 6, 10, 13, 17},正例 3/6,反例 3/6
D2(色泽=乌黑) = {2, 3, 7, 8, 9, 15},正例 4/6,反例 2/6
D3(色泽=浅白) = {5, 11, 12, 14, 16},正例 1/5,反例 4/5
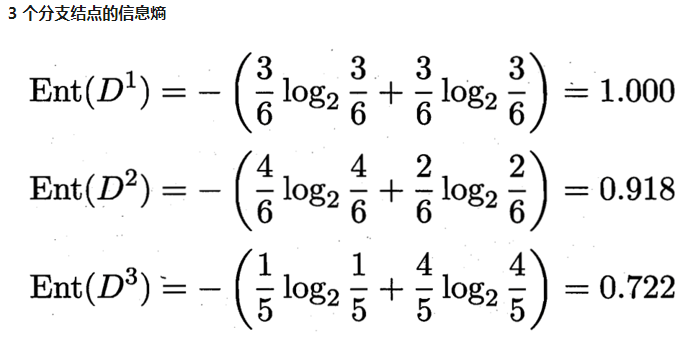
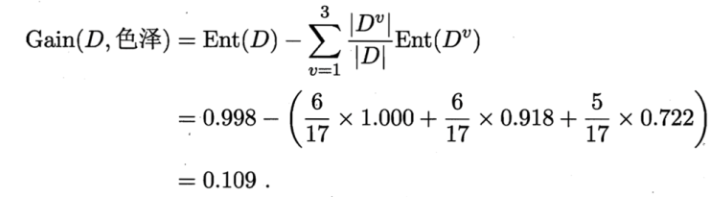

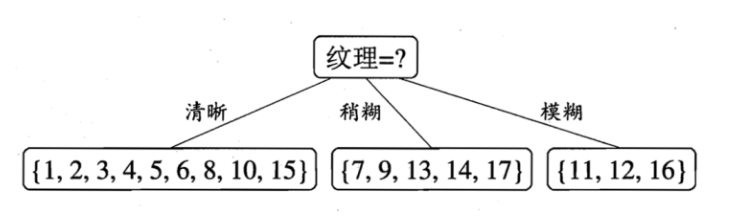
例如 D1(纹理=清晰) = {1, 2, 3, 4, 5, 6, 8, 10, 15},第一个分支结点可用属性集合{色泽、根蒂、敲声、脐部、触感},基于 D1各属性的信息增益,分别求的如下:

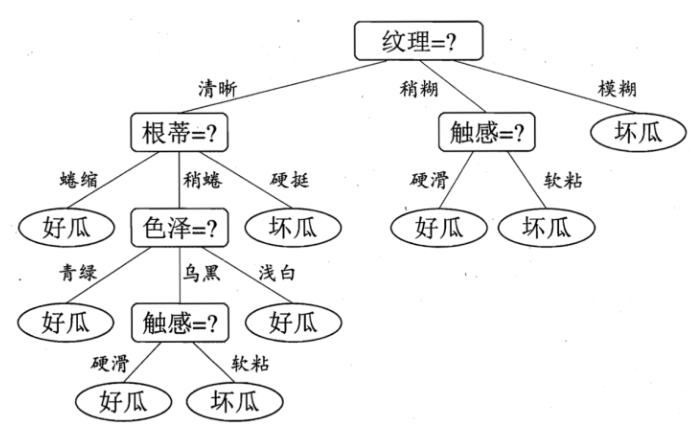

C4.5算法
有了ID3算法,为什么还有C4.5呢?那是因为ID3算法有一定的缺陷,比如我们用数据集中的编号作为候选划分属性,算出的“编号”信息增益是0.998,也就是说当有一个预测样本,知道编号后,其余特征没有用,这个是十分不合理的。C4.5算法是如何解决的呢?
那就是信息增益率,公式为:
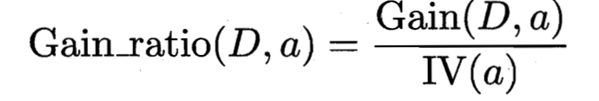
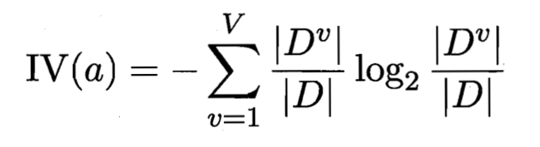
举例
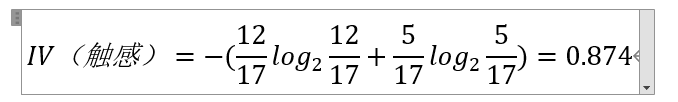
参考: