[TOC]

cost Function和regularization

监督学习的目的就是要最小化cost Function. 但这个过程中往往会产生些错误，如overfit，而正则化的存在是通过调整正则化参数而达到想要的目的

L1-norm和L2-norm均可以作为cost function 或 regularization

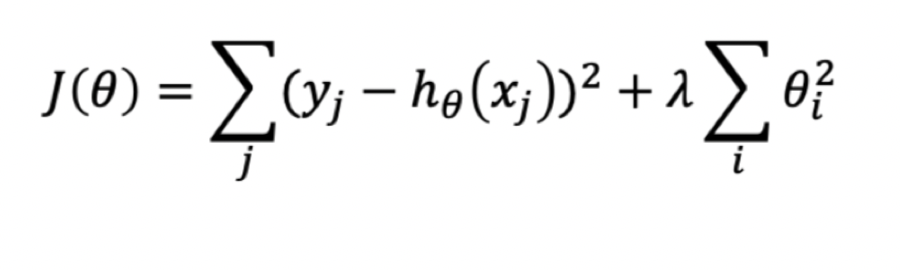
cost Function

log对数cost Function---logstic regression

square loss ----- 最小二乘，OLS----L2-norm

Hinge Loss ----- SVM

Exponential Loss ----- adaBoost

0-1 Loss

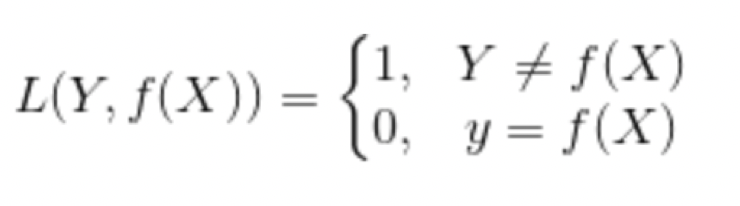
绝对值 Loss ---- L1-norm

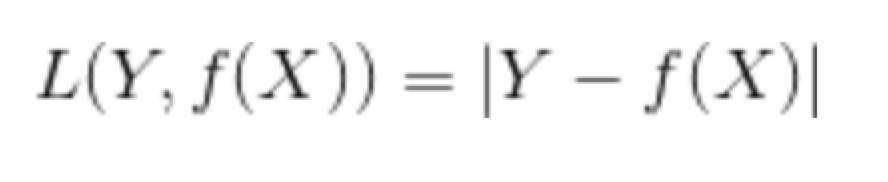
对比图 ---- 机器学习基石中，林轩田老师讲过

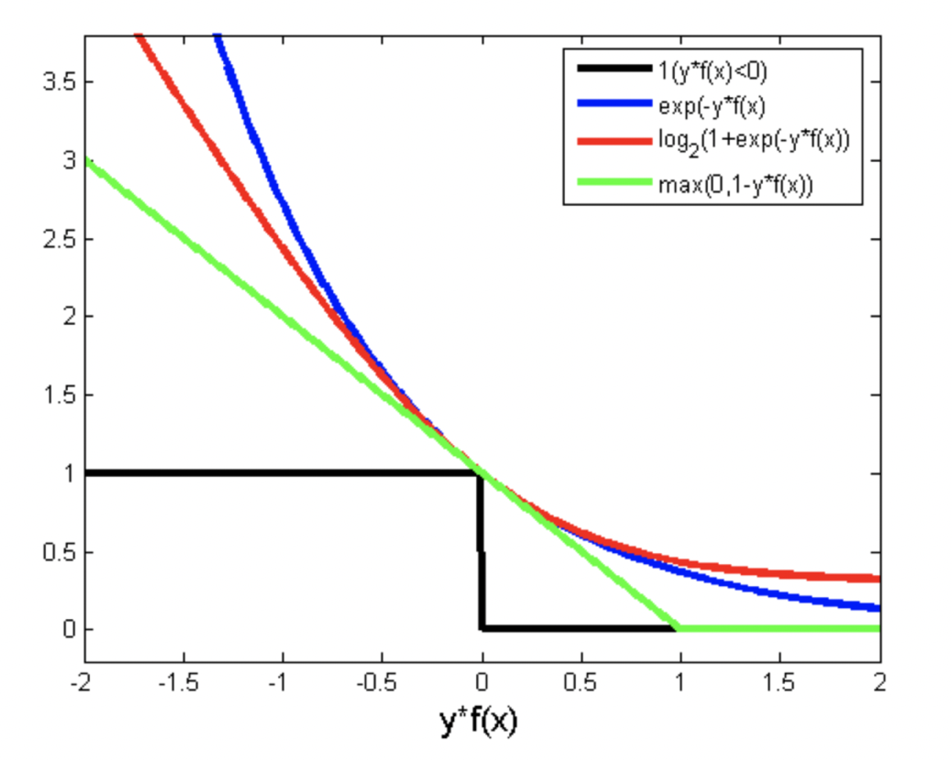
regularization 函数

将任意向量x 的l_p-范数定义为:

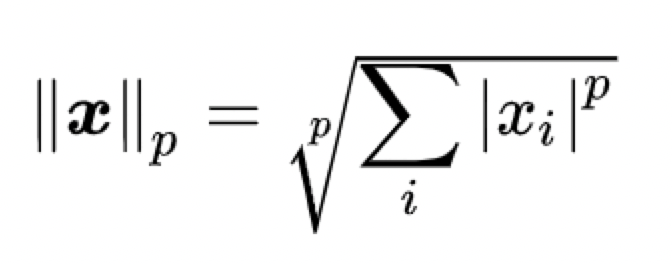
L0范数

根据上图有

等同于

往往表示向量中不为0的个数，如果用L0范数来正规化，那么我们就希望矩阵大部分都为0，即稀疏。这个问题在数学上是一个NP-hard问题，即直接求解很复杂

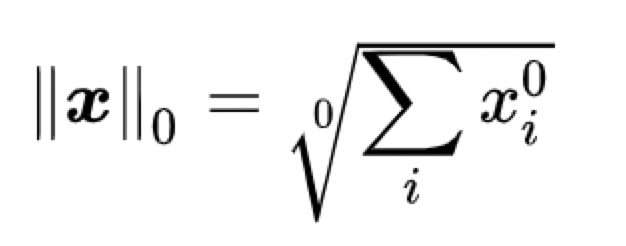
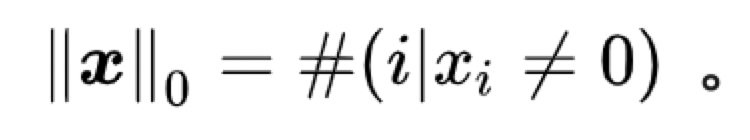
L1范数

代表向量中所有元素绝对值之和
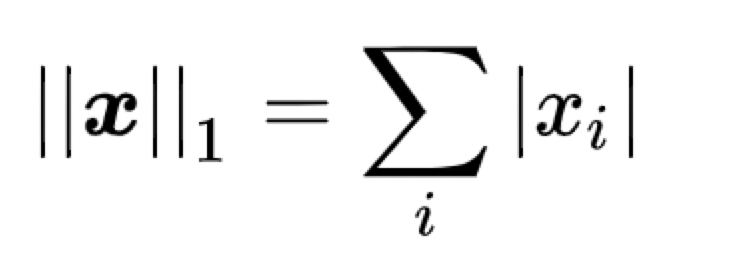
L1-regularization作为正则项-----lasso回归

对于L1来说，有如下图--几何解释

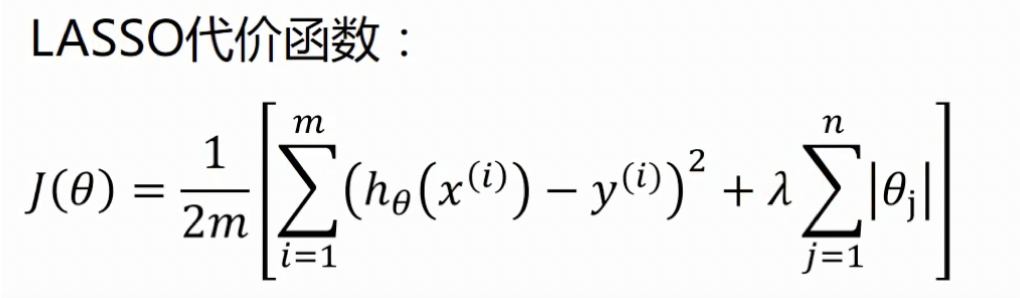
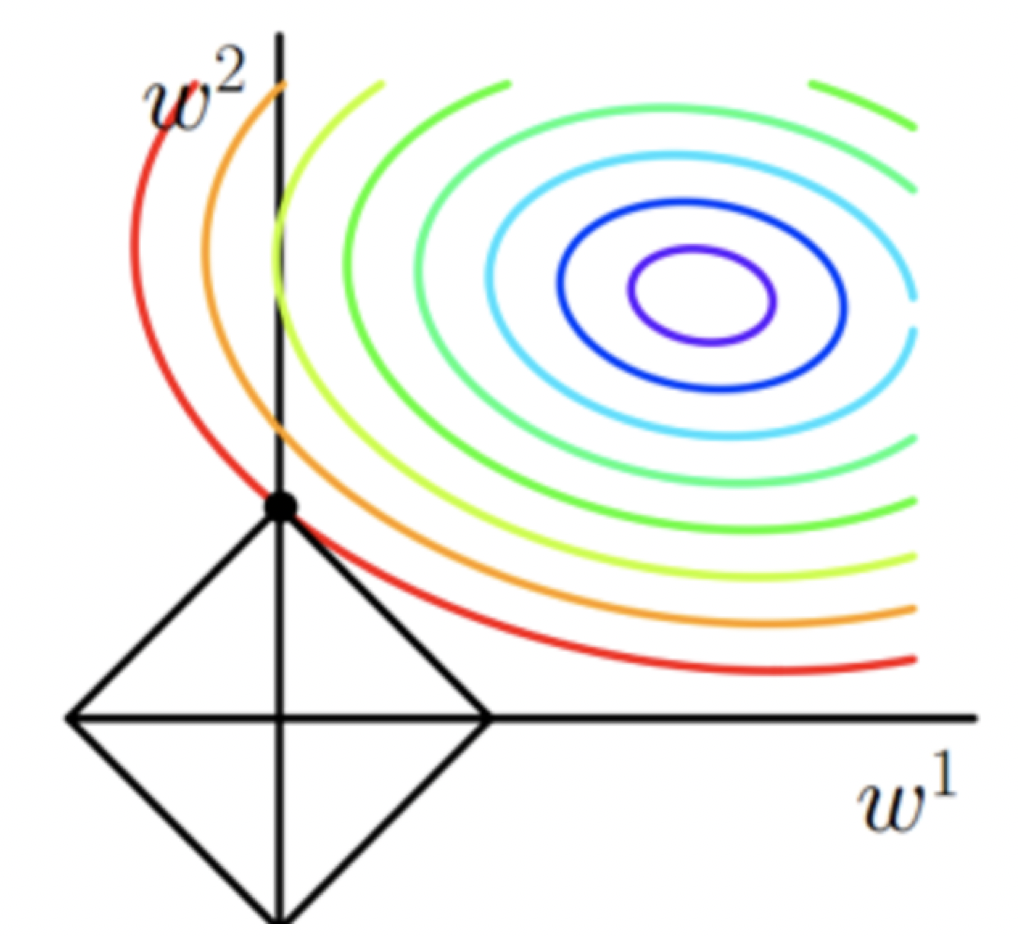
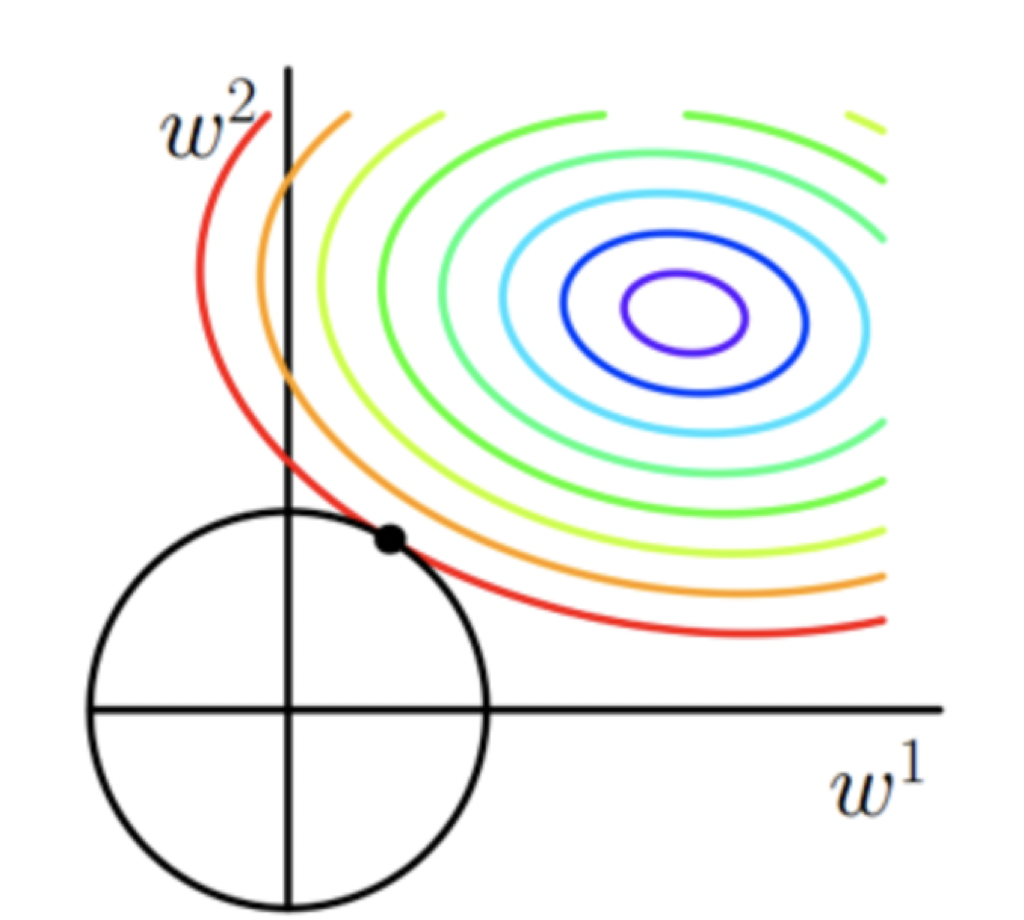
假设有w1,w2两个参数，圆圈代表着cost Function，圆点就是cost Function的最小值，往外增大，每一圈上的数值相等。而图中正方形则是我们的L1正规化式子|x|,那么，当圆形和正方形相交的地方就是我们要求的cost Function+regularization的最小值。而着这一数值往往存在于坐标轴上，即(w1,0)或(0,w2)，这时候就会产生稀疏。L1会倾向于产生少量特征，其他特征都为0，L1范数的最优解比L2少，但往往是最优解。L1会把不重要的参数直接置0

L2范数

L2-norm

同理，代表向量中所有元素的平方和
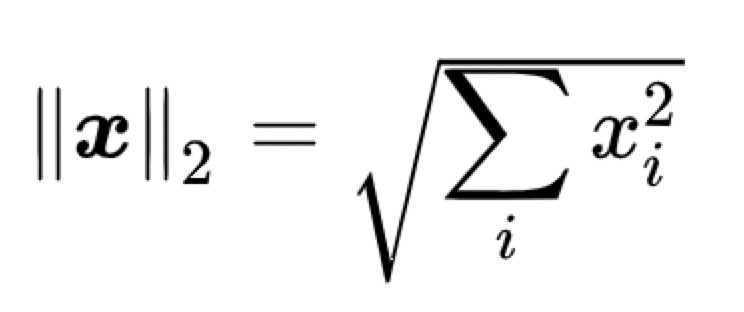
L2-norm作为正则项的代价函数----岭回归(ridge)

类似的

相交点往往不是在坐标轴上，所以ridge往往是平滑的，L2更多的是用于防止overfit，因为其交点往往不是稀疏，所以=参数变小，模型变简单。

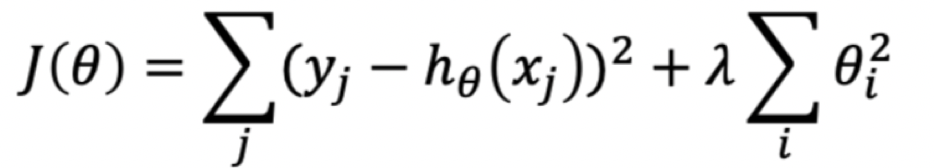
参考资料

blog.csdn.net/sinat_26917…
zhuanlan.zhihu.com/p/58883095
www.csuldw.com/2016/03/26/…
www.zhihu.com/question/20…
zhuanlan.zhihu.com/p/26884695
www.jianshu.com/p/de05e6745…
www.youtube.com/watch?v=t2E…
www.zhihu.com/question/26…