SVM与对偶Perceptron

最近上课讲到SVM，太久没回顾了有点蒙，之前笔记之记在纸上，甚是不便，今日便将其整理upload。

由perceptron引发的这篇文章

普通perceptron

loss function：

梯度更新则有：

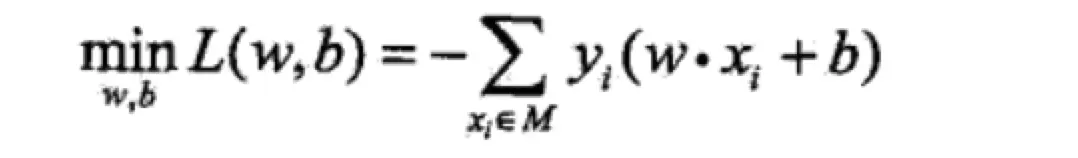
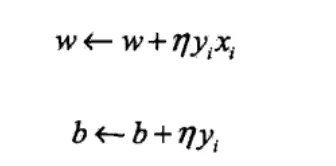
对偶perceptron

我们可以相对原本的perceptron算法换个思路去思考，因为我们有梯度更新如下，即最终的w = 所有ηyx相加，b = 所有ηy相加，那么我们是如何确定每次运算是否更新w，b，就是根据是否犯错(violate)，一旦犯错，就必须要更新。

那么我们就可以用一个东西去记录犯错次数

如上图，我们用α = nη 来表示犯错次数，其中n是有下标的,n_i表示的是第i个点的犯错次数。

如上截图，前面还有一些无关紧要的东西就不截了，这里可以看出每次更新α<-α + ηx1,这里的乘1代表i点犯错次数加一。

另外，用对偶perceptron还有个好处就是，能用gram矩阵，能节省<xi,xj>之间的内积计算
根据《统计学习方法》,有例子更容易上头：

对照这最后一个迭代过程来看，就很容易理解整个dual perceptron了。

SVM

SVM分为hard-margin SVM 和 soft-margin SVM

hard-margin SVM

由perceptron引发了一个问题，就是临近分界线的点往往会导致perceptron不断的update，因为存在多个线可以分割平面

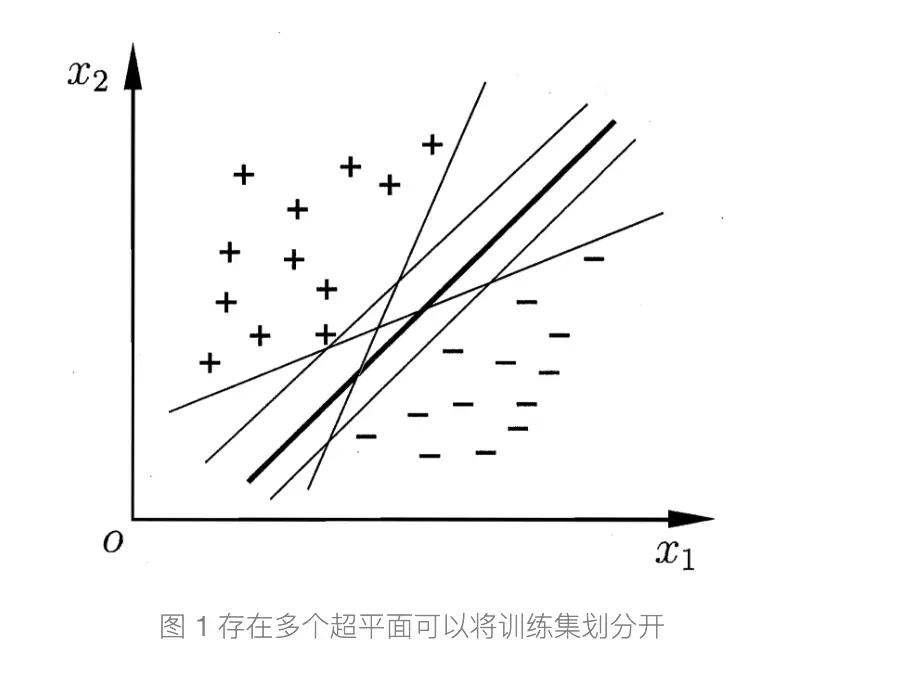
SVM可以好好的解决这个问题，比较简单所以简略记录，具体可看参考资料第一个网址

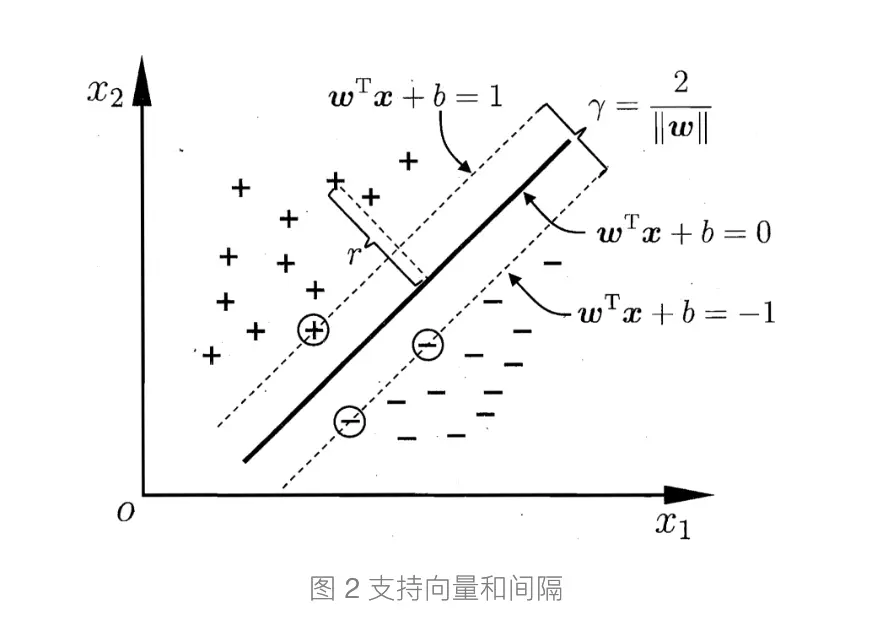
我们可以看到wx+b = 0
(这里图中margin是几何距离，几何函数是y(wx+b)/||w||)
(函数函数是，y(wx+b)，这也说明了几何距离是固定的，几何函数是可以不断增大的)
这条就是我们margin里面的中线了，我们要做的就是最大化这个margin，而在最大化margin后，刚好在margin线上的点就是SV(support vector)
这里解释下为何margin = 2/||w||,根据平行线公式 |c1 - c2|/(sqrt(A^2 + B^2))就可以得到啦。然后根据江湖规矩，将最大化变为最小化，即max(2/w) ---> min(w/2)一样求极值，然后为了方便运算就编程min(w/2)

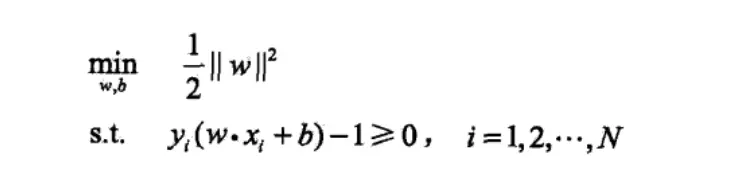
就有我们的目标函数及其约束条件了，这里的约束条件就是要求这个点必须正确分类，只有正确分类这个约束条件才成立

二次规划方程

QP问题可以用专用的QP solver来解决，很快，但必须是QP问题
如果目标函数是凹的（最大化问题）或凸（最小化问题）并且约束集是凸的，那么该程序称为凸，并且在大多数情况下可以使用来自凸优化的通用方法。
如果目标函数f是线性的并且约束空间是多面体，则问题是线性规划问题，其可以使用诸如单纯形法之类的众所周知的线性规划技术来解决。
如果目标函数是二次的且约束是线性的(一次方关系)，则使用二次规划技术
如果目标函数是凹函数和凸函数的比率（在最大化情况下）并且约束是凸的，那么可以使用分数规划技术将问题转化为凸优化问题。
不是QP，kernel，dual都没法用
根据参考资料中的SVM

我们的SVM需要满足KKT条件才能在对偶化后得到最优值(往下看)

拉格朗日乘子----化约束为无约束

回到上面这个最小化问题上面，因为有约束条件的存在，解方程显得不方便，我们可以用到拉格朗日乘子来将之转换为无约束。首先要做的就是将约护士条件乘上拉格朗日乘子(这里是α)加入到目标函数之中，如下图：

这里α>=0，这个式子叫拉格朗日函数。

接下来我们要将SVM转换为无约束条件的式子。即我们把SVM转化掉，但求得东西和原来的要一毛一样。怎么做呢。看上图下面的claim：
先别纠结为什么要max，为什么要min，且听我说。
分两种情况，即满足约束条件和不满足约束条件的, 约束条件(y(wx+b) - 1 >= 0),这图里是z代替x，是因为z代表的是特征转换(不是kernel,是feature transform)后的数据

如果满足约束条件，我们拉格朗日函数的后一项，即∑(α(1-y(wx+b))) 必然<=0, 因为α是>=0的，那么当max 拉格朗日函数时，最大的是什么，当然就只能是我们的w平方/2啦，即上图中的□，而此时在min，看看，是不是跟原来的问题一毛一样。对了，此时将得到最优解，而这个时候α(1-y(wx+b))=0,这个也是构成KKT条件的一部分。
那么如果不满足约束条件呢，图中所示，∑(α(1-y(wx+b)))中，α>=0，而后面那一项也>0，如果max，那就是+∞，这个时候我们min是无意义的。
基于上述两点，我们可以得到min(max 拉格朗日函数)就等于原函数(在约束条件下)，不满足约束条件(不在可行区域内的)冇意义。
至此，已经转化为无约束的函数。

拉格朗日对偶化

这里先丢点东西出来：

目标函数对原始问题是极大化,对对偶问题则是极小化
原始问题目标函数中的收益系数（优化函数中变量前面的系数）是对偶问题约束不等式中的右端常数,而原始问题约束不等式中的右端常数则是对偶问题中目标函数的收益系数
原始问题和对偶问题的约束不等式的符号方向相反
原始问题约束不等式系数矩阵转置后即为对偶问题的约束不等式的系数矩阵
原始问题的约束方程数对应于对偶问题的变量数,而原始问题的变量数对应于对偶问题的约束方程数
对偶问题的对偶问题是原始问题
(视频link在参考资料中)

我们先庸俗点讲如何对偶化：

看看上图，左边的使我们的无约束拉格朗日函数，而右边的使我们的目标函数，那么我们如何得出来的>=？？？
我们先看上图的第一幅图，我们先假设有一个固定的α'在右边式子，那么因为我们左边的式子是max α，所以说他是最大的没问题吧，那么max >= any 大于任意一个α’也没问题吧，那么就有左边的 >= 右边的。
现在有min(max L) >= min(L), 那么我在这个基础上，往右边的再添加上max形成上图的第二幅图也是不是应该成立。(切记这里的系数要求)

我们刚刚推导的东西存在的>=号，其实叫弱对偶性，那如果是强对偶性(=)就意味着我们可以用对偶问题来替代原问题来解答(强对偶性，最优解相等)
我们的问题是二次规划问题，做最佳化的人推导一下发现，对于二次规划问题来说，如果我们要解的问题是convex的凸的，原来问题有解的(原来条件下能找到最优值)，有线性的约束条件------>就有强对偶关系。

原问题(SVM)为凸的
原问题有解
优先性约束
满足这三个条件的就有强对偶关系，我们也就可以用右边的对偶问题来代替原本的问题

然后，我们进一步求解，对b求导并=0：

我们把得到的这个东西代回原式子中便会得到：

然后接着对w操作：

就会得到

最后那个式子使我们目前的目标函数
然后我们要通过QP solver求出α，首先先把max转换为min：

求出α：

这里的Qn,m经常是稠密的，不为0，所以经常要用special 的sovler来解决
那么接下来，求得α了，如何求w和b呢，使用KKT条件求出
这里先弄个关系图

所有极值都肯定满足KKT条件,反之不一定

其实上述4个KKT条件中，我们只用到第三个和第四个，第四个称为互补松弛性，怎么来的呢，记得上面推导为什么要min(max拉格朗日函数)，就是因为在可行域内，当第四个条件里的公式=0，我们才有最大的拉格朗日函数。由此，根据这个条件，当α>0时，不就有1-y(wx+b) = 0吗，即b = y-wx, 这不就是我们的SV吗，所以我们就可以求得w和b，只需要保留SV，其他点都可以不要。

。对偶问题的存在是为了解决原问题中维度过大而导致的复杂度激增。

(这里的对偶形式，是经过QP solver后的结果)如上图中原问题中，求解复杂度与w的维度有关即d~ + 1， d为什么有个~呢，是因为这里代表的是feature空间转换成更高维的空间后的结果(不是kernel)，而对偶问题就是跟样本数量有关，所以如果做线性分类，样本数量高于维度的话，完全可以用原问题直接求解。可如果做非线性分类，那么必然涉及到加kernel的操作，会提升到高纬度(kernel往下看),那就要用对偶问题来做了。
从物理意义上来讲，原来的问题做特殊的自由放缩，对偶问题是找到α>0时是SV，并用其来重建Margin

然而，上述的对偶问题真的跟d~没关系了吗，不见得(只能说，基本无关系)，Q_d里面还含有Z的内积
好了，事情来到这里，我们要通过加入kernel来使他彻底跟d~无关(kernel这一部分下一part讲)

kernel

由于对偶SVM经常解决的是non-linear问题，所以就是用 Φ(x)来代替fearture transform后的数据，x->Φ(x)，其实是两个步骤，先进行空间转换，再进行内积，现在问题就是我们这个Φ(x)要进行内积，那必然是比原来空间的数据进行内积还要复杂，那该怎么解决呢，我们能不能把这两个步骤联合起来呢。
kernel = feature transform + inner product

这里有一例子，

所以有了这个转换概念后，我们就可以用来解决我们刚才的问题了。

这里zz我们用K(x,x)来代替，那么同理，我们不再用z空间的数据，那求b啊啥的都得用kernel代替。这样搞，我们就避免了要在z空间做内积的计算复杂了(我们之前所有的非线性东西，用的都是z空间的数据，z空间是将x空间的数据进行维度转换得来的，如加个平方啊，三次方啥的)
接下来我们还是可以用QP来解决kernel SVM：

polynomial kernel，高斯kernel暂时不写，用到的时候再补充。

聚类，分类常用kernel
kernel其实就是将低纬度映射到高纬度，从而能找出一个能够正确划分样本的超平面（西瓜书）原始空间有限维度，那么一定存在能被划分的高纬度空间
高斯核函数也叫径向基核函数RBF kernel----一个球代表着一堆SV的高斯核函数的线性组合
高斯核函数能映射到无限维度

if your number of features is really large compared to the training sample, just use linear kernel; if your number of features is small, but the training sample is large, you may also need linear kernel but try to add more features; if your feature number is small (10^0 - 10^3), and the sample number is intermediate (10^1 - 10^4), use Gaussian kernel will be better.----抄自stackflow
LogReg和SVM 均为线性，加核函数可以变为非线性(普通改变特征也行，x+x1--->x^2+x1^2之类的)
对SVM进行对偶是因为要改变算法的复杂度，维度有关---->样本数量有关。也就是说，如果做的线性回归，feature小于样本数量就不用对偶，要是做非线性回归，那么必然涉及到升维度，如高斯核函数，那么此时就要进行对偶，对偶后要完全消除维度的影响提高效率就得加入核函数。
不是QP，kernel，dual都没法用
核函数和SVM没必然联系，对于核函数吴恩达解释一个样本点出现在landmark附近的概率(相似程度)