==为了对信息(特征？)进行量化处理，然后再选定以什么作为标准，期望(纯度越来越高)信息增益越大==

[TOC]

决策树 特征选择

“信息熵”是度量样本集合不确定度（纯度）的最常用的指标
熵---->不确定性的量度 熵越高，不确定性越大 越随机，概率低，熵越大 熵越大，信息量越大

1. 信息熵

信息熵公式(information entropy):

其中p(x_i)代表随机事件X为x_i的概率
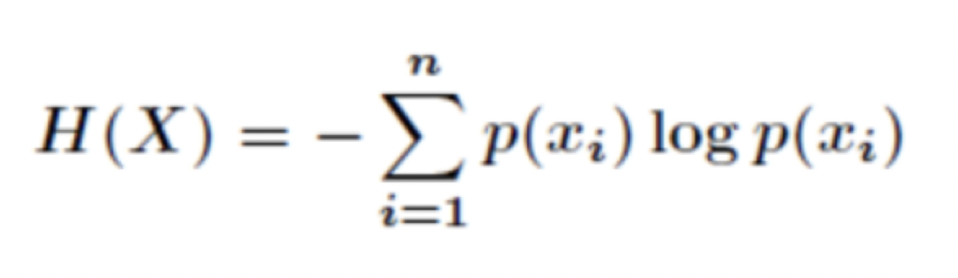
信息熵代表两个东西：

1. 信源的平均信息量
2. 编码所有符号X所需的位数(如编码所有X要 3bit/字节)

信息量：(时间发生概率越大，信息量越小，如太阳从东边升起，信息量小)
对于两个独立事件x, y来说 信息量x, y同时发生时的信息量H(x,y) = H(x) + H(y)
而x, y同时发生概率等于P(x,y) = p(x) * p(y)
(当为对数关系时，才有log(xy) = log(x) + log(y))
所以有

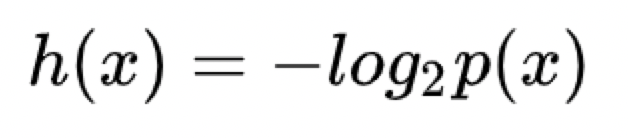
为啥是以2为低？ 传统。。。。(只要保证0-1之间能正确表达概率越小，信息量越大即可)

为啥是负的关系？ 保证为>=0

信息熵指的是对可能出现的信息量的==期望==（也就是不确定性）：

转换即得到一开始的公式。

越复杂，对应于每种情况的概率就越小，信息熵就越大(不确定性越大)

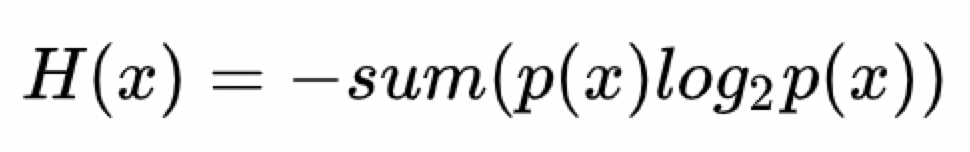
2. 条件熵

条件熵定义： X给定条件下，Y的条件概率分布的熵对X的数学期望

这个条件熵，是指在给定某个数（某个变量为某个值）的情况下，另一个变量的熵是多少，变量的不确定性是多少？
就是有条件的信息熵，在信息熵的基础上加上条件
P(y|x) = .....

注意这里的x和y都是变量，所以有多个值
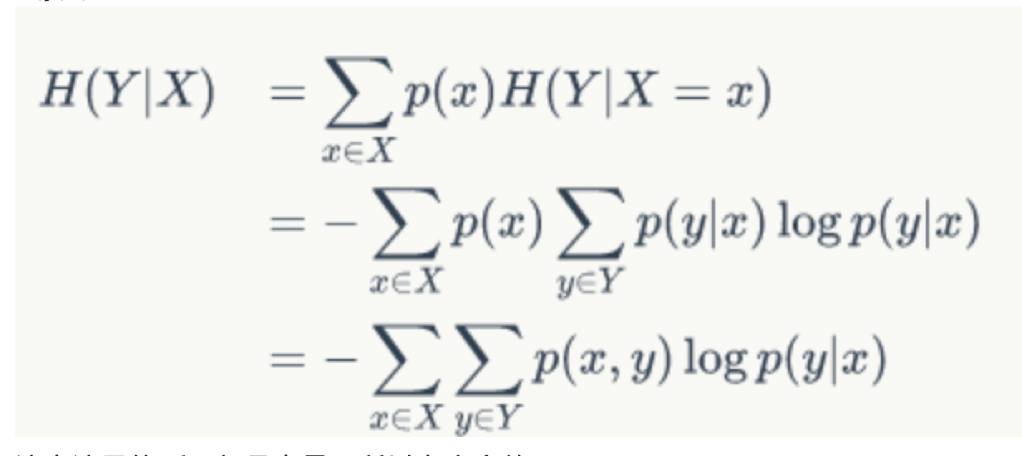
先把条件分解，再求每个条件下的H(x)，以及该条件的概率p(x)，然后对应乘起来再相加即可。 具体例子看 zhuanlan.zhihu.com/p/26551798

3. 信息增益

在决策树算法的学习过程中，信息增益是特征选择的一个重要指标，它定义为一个特征能够为分类系统带来多少信息，带来的信息越多，说明该特征越重要，相应的信息增益也就越大。

信息增益 = 信息熵 - 条件熵
计算根节点的信息熵(也就是总体的分类)，然后再根据条件求条件熵，相减得到信息增益. (==具体参考参考资料信息熵==) 得到的结果越大，说明信息增益越大

信息增益代表着在一个条件下，信息复杂度（不确定性）减少的程度。

那么对应到决策树结点上，怎么选择特征，就是选了这个特征后，信息增益最大(不确定性减少程度最大)，就是分支里的每一个都是一类(err rate最小)

参考资料：

zhuanlan.zhihu.com/p/26486223 ID3
zhuanlan.zhihu.com/p/26760551 信息熵
zhuanlan.zhihu.com/p/26551798 条件熵
zhuanlan.zhihu.com/p/26596036 信息增益
zhuanlan.zhihu.com/p/26454072