1. 算法思想
归并排序和快速排序一样,都是应用分治法思想的排序算法。假设对一个记录序列进行升序排序,归并排序的基本思想是:
- 划分:将待排序序列
,
, ...,
划分为两个长度相等的子序列
, ...,
和
, ...,
- 求解子问题:分别对这两个子序列进行排序,得到两个有序子序列
- 合并:将这两个有序子序列合并成一个有序序列
2. 具体过程
- 首先执行划分过程,将序列划分为两个子序列,如果两个子序列的长度为 1,则划分结束,否则继续重复该步骤执行划分过程,最后将具有 n 个待排序记录的序列划分成 n 个长度为 1 的有序子序列
- 然后执行合并,将两个有序子序列合并成一个有序子序列,直到得到一个长度为 n 的有序序列
3. 过程图示
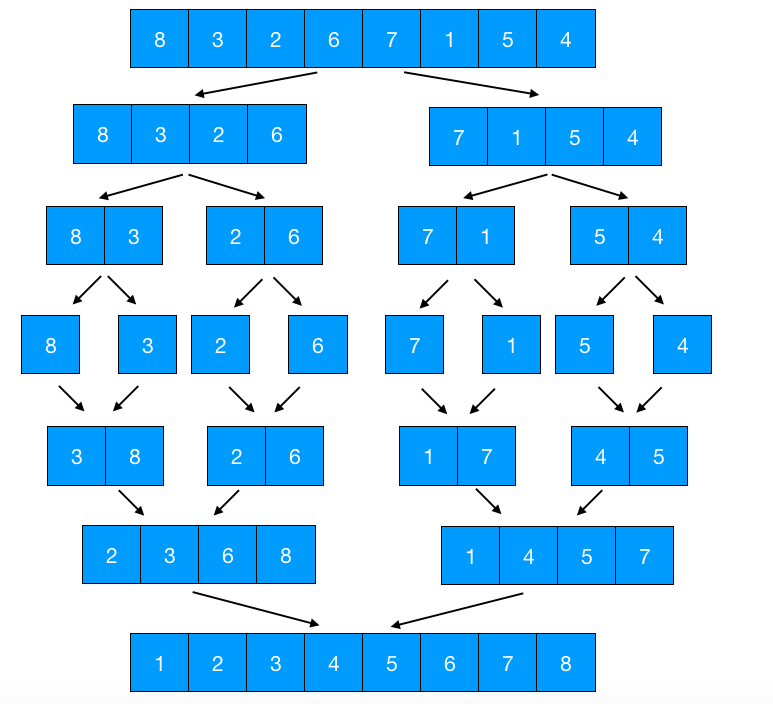
4. 代码实现
Java 代码实现:
/**
* @author created by linjunhao
* @date 2020/3/27
* @description 归并排序
*/
public class MergeSort {
/**
* 归并排序
*
* @param values
* @param start
* @param end
*/
public void sort(int[] values, int start, int end) {
int middle;
//临时数组
int[] temps = new int[values.length];
//递归的边界条件
if (start == end) {
return ;
} else {
//划分
middle = (start + end) / 2;
//求解子问题1,归并排序前半个子序列
sort(values, start, middle);
//求解子问题2,归并排序后半个子序列
sort(values, middle + 1, end);
//合并两个有序子序列,结果存在临时数组中
merge(values, temps, start, middle, end);
//将有序序列传回数组
for (int i = start; i <= end; i++) {
values[i] = temps[i];
}
}
}
/**
* 合并子序列
*
* @param values 待排序序列
* @param temps 临时数组
* @param start
* @param middle
* @param end
*/
public void merge(int[] values, int[] temps, int start, int middle, int end) {
int i = start;
int k = start;
int j = middle + 1;
while (i <= middle && j <= end) {
//取两个子序列中较小值放入到临时数组中
if (values[i] <= values[j]) temps[k++] = values[i++];
else temps[k++] = values[j++];
}
//若第一个子序列没处理完,则需要把子序列中剩余的记录放入到临时数组中
while (i <= middle) {
temps[k++] = values[i++];
}
//若第二个子序列没处理完,则需要把子序列中剩余的记录放入到临时数组中
while (j <= end) {
temps[k++] = values[j++];
}
}
}
5. 算法分析
- 归并排序的时间复杂度为