学习JavaScript数据结构与算法【第三版】 阅读笔记
1.栈
1.1 特点
- 后进先出
- 拥有push/pop/isEmpty/size/peek/toString/clear方法
1.2 实现
class Stack {
constructor() {
this.items = {};
this.count = 0;
}
// 入栈
push(el) {
this.items[this.count] = el;
this.count++;
}
// 大小
size() {
return this.count;
}
// 是否为空
isEmpty() {
return this.count === 0;
}
// 出栈
pop() {
if (this.isEmpty()) return undefined;
this.count--;
const result = this.items[this.count];
delete this.items[this.count];
return result;
}
// 查看栈顶
peek() {
if (this.isEmpty()) return undefined;
return this.items[this.count - 1];
}
// 清空栈
clear() {
this.items = {};
this.count = 0;
}
// 打印栈
toString() {
if (this.isEmpty()) return '';
let objString = this.items[0];
for (let i = 1; i < this.count; i++) {
objString += `,${this.items[i]}`;
}
return objString
}
}
1.3 其他
- 也可以数组写法,相对简单但是开销大
- 变量私有化可以用Symbol和WeakMap解决
1.4 应用示例
十进制转换为二进制
function decimalToBinary(decimal){
const stack = new Stack();
let rem, binary = '';
while(decimal > 0 ){
rem = decimal % 2;
decimal = Math.floor(decimal/2);
stack.push(rem);
}
while(!stack.isEmpty()){
binary += stack.pop()
}
return binary;
}
消消乐
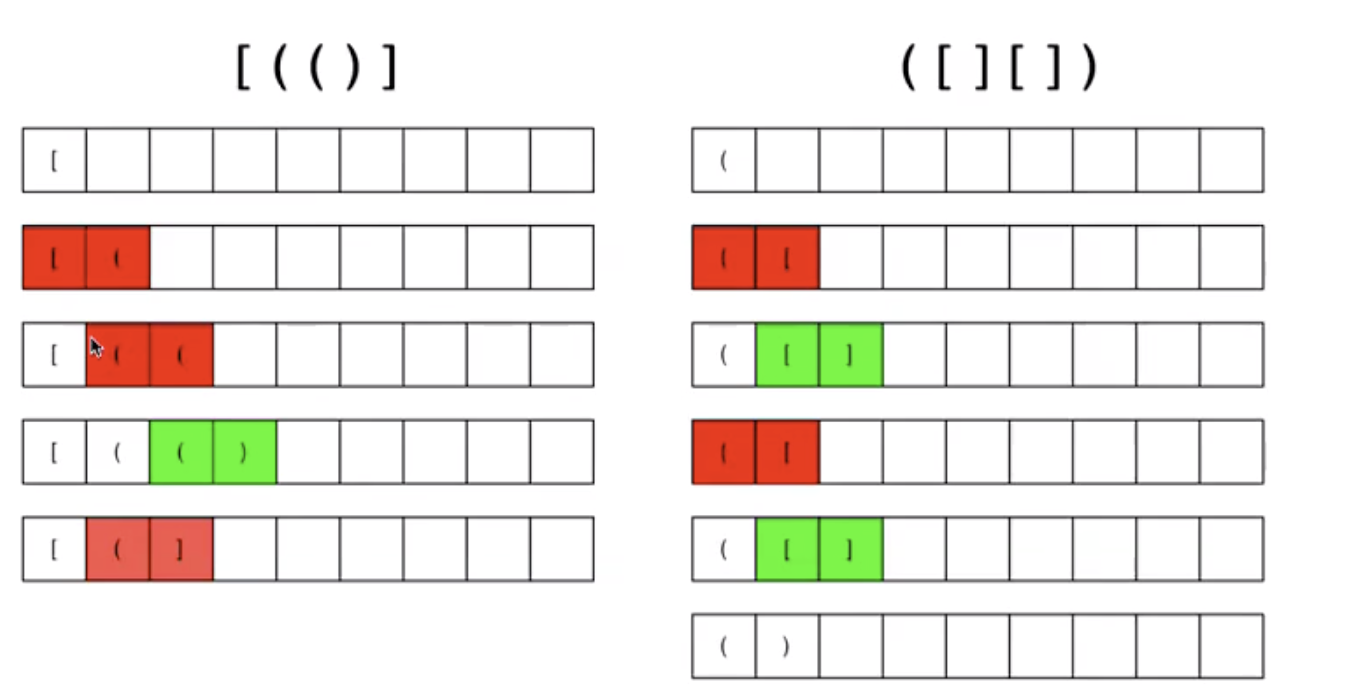
function pair(str) {
const stack = new Stack();
const pairArr = {
'{': "}",
'[': ']',
'(': ')'
};
for(let i of str){
const peek = stack.peek();
if(pairArr[peek] === i){
stack.pop()
}else{
stack.push(i)
}
}
return stack.size() === 0;
}
2. 队列
2.1 普通队列
2.1.1 特点
- 先进先出
- 拥有push/pop/isEmpty/size/peek/toString/clear方法
2.1.2 实现
class Queue {
constructor() {
this.items = {};
this.count = 0; //记录队列的最后面
this.lowestCount = 0; // 记录队列的最前面
}
// 入队
enQueue(el) {
this.items[this.count] = el;
this.count++;
}
// 出队
delQueue() {
if (this.isEmpty()) return undefined;
const result = this.items[this.lowestCount];
delete this.items[this.lowestCount];
this.lowestCount++;
return result;
}
// 是否为空
isEmpty() {
return this.size() === 0;
}
// 尺寸
size() {
return this.count - this.lowestCount;
}
// 查看队头
peek() {
if (this.isEmpty()) return undefined;
return this.items[this.lowestCount];
}
// 清空队列
clear() {
this.items = {};
this.count = 0;
this.lowestCount = 0;
}
// 打印
toString() {
if (!this.isEmpty()) return '';
let string = this.items[this.lowestCount];
for (let i = this.lowestCount + 1; i < this.count; i++) {
string += `,${this.items[i]}`
}
return string;
}
}
2.1.3 应用示例
击鼓传花游戏,每次鼓声停止手里拿花的那个被淘汰退出,然后从下一个继续开始,知道剩余最后一个获胜
function hotPhoto(nameList){
const queue = new Queue();
const deleteName = [];
nameList.forEach(name => {
queue.enQueue(name);
})
while(queue.size() > 1){
const loopNum = Math.floor(Math.random() * 10);
for(let i=0; i<loopNum; i++){
queue.enQueue(queue.delQueue());
}
deleteName.push(queue.delQueue());
console.log(`${deleteName[deleteName.length - 1]}被淘汰`)
}
const warnName = queue.delQueue();
console.log(`最后胜利者:${warnName}`)
return {
deleteName,
warnName,
}
}
const result = hotPhoto(
['小明', '小红', '小王', '小李', '小花', '小龙']
)
小明被淘汰
小龙被淘汰
小李被淘汰
小红被淘汰
小花被淘汰
最后胜利者:小王
2.2 双端队列
2.2.1 特点
- 允许从前端和后端添加移除的特殊队列
- 可以获取第一个和最后一个元素
2.2.2 实现
class Dequeue {
constructor() {
this.items = {};
this.count = 0;
this.lowestCount = 0;
}
// 前端增加
addFront(el) {
if (this.isEmpty()) {
return this.addBack(el);
}
// 前面有空位
if (this.lowestCount > 0) {
this.lowestCount--;
this.items[this.lowestCount] = el;
} else {
for (let i = this.count; i > 0; i--) {
this.items[i] = this.items[i - 1]
}
this.count++;
this.lowestCount = 0;
this.items[0] = el;
}
}
// 后端增加
addBack(el) {
this.items[this.count] = el;
this.count++;
}
// 前端删除
removeFront() {
if (this.isEmpty()) return undefined;
const result = this.items[this.lowestCount];
delete this.items[this.lowestCount];
this.lowestCount++;
return result;
}
// 后端删除
removeBack() {
if (this.isEmpty()) return undefined;
const result = this.items[this.count - 1];
delete this.items[this.count - 1];
this.count--;
return result;
}
//前端第一个元素
peekFront() {
if (this.isEmpty()) return undefined;
return this.items[this.lowestCount];
}
// 后端第一个元素
peekBack() {
if (this.isEmpty()) return undefined;
return this.items[this.count - 1];
}
// 是否为空
isEmpty() {
return this.size() === 0;
}
// 尺寸
size() {
return this.count - this.lowestCount;
}
// 清空
clear() {
this.items = {};
this.count = 0;
this.lowestCount = 0;
}
// 打印
toString() {
if (this.isEmpty()) return '';
let objString = this.items[this.lowestCount];
for (let i = this.lowestCount + 1; i < this.count; i++) {
objString += `,${this.items[i]}`
}
return objString;
}
}
2.2.3 应用示例
回文判断
function palindromeChecker(string){
if(typeof string !== 'string' || string.length === 0) return false;
const dequeue = new Dequeue();
const dealStr = string.toLowerCase().replace(/\s+/g, '');
[...dealStr].forEach(e => dequeue.addFront(e));
let isEqual = true, pre, next;
while(isEqual && dequeue.size() > 1){
pre = dequeue.removeFront();
next = dequeue.removeBack();
if(pre !== next) isEqual = false;
}
return isEqual;
}
3. 链表
3.1 单向链表

3.1.1 特点
- 用一组任意的内存空间去存储数据元素(这里的内存空间可以是连续的,也可以是不连续的)
- 每个节点(node)都由数据本身和一个指向后续节点的指针组成
- 最后一个节点的指针指向空(NULL)
3.1.2 实现
class Node {
constructor(ele) {
this.ele = ele;
this.next = null;
}
}
class LinkList {
constructor() {
this.head = null;
this.count = 0;
}
// 在链表尾部插入节点
push(ele) {
const node = new Node(ele);
if (this.head === null) {
this.head = node;
} else {
let current = this.head;
while (current.next !== null) {
current = current.next;
}
current.next = node;
}
this.count++;
}
// 移除其中一个节点
removeAt(index) {
if (index >= 0 && index < this.count) {
let current = this.head;
if (index === 0) {
this.head = current.next;
} else {
const previous = this.getElementAt(index - 1);
current = previous.next;
previous.next = current.next;
}
this.count--;
return current.ele;
}
return undefined;
}
// 得到节点
getElementAt(index) {
if (index >= 0 && index <= this.count) {
let node = this.head;
for (let i = 0; i < index && node !== null; i++) {
node = node.next;
}
return node && node.next;
}
return undefined;
}
// 插入元素
insert(ele, index) {
if (index >= 0 && index <= this.count) {
const node = new Node(ele);
if (index === 0) {
const current = this.head;
node.next = current;
this.head = node;
} else {
const previous = this.getElementAt(index - 1);
const current = previous.next;
previous.next = node;
node.next = current;
}
this.count++;
return true;
}
retun false;
}
// 返回一个元素的位置
indexOf(ele) {
let current = this.head;
for (let i = 0; i < this.count && current !== null; i++) {
if (this.equalFn(ele, current.next)) {
return i;
}
current = current.next;
}
return -1;
}
// 从链表中移除元素
remove(ele) {
const index = this.indexOf(ele);
return this.removeAt(index);
}
// 长度
size() {
return this.count;
}
// 是否为空
isEmpty() {
return this.size() === 0;
}
//获取第一个
getHead() {
return this.head;
}
// 打印
toString() {
if (this.head === null) return '';
let objString = this.head.ele;
let current = this.head.next;
for (let i = 1; i < this.size() && current !== null; i++) {
objString += `,${current.ele}`;
current = current.next;
}
return objString;
}
}
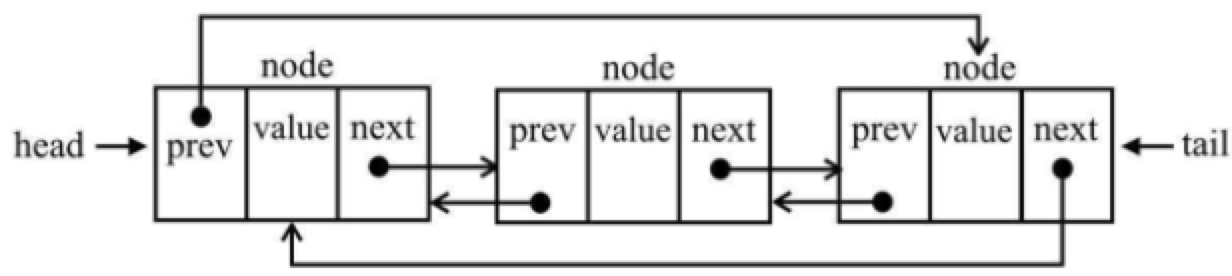
3.2 双向链表

3.2.1 特点
- 链接双向的,一个节点一端链向上一个节点,另一个端链向下一个节点
3.2.2 实现
3.2.2 实现
class DoubleNode extends Node{
constructor(ele){
super(ele);
this.pre = null;
}
}
class DoubleLinkList extends LinkList{
constructor(){
super();
this.tail = null;
}
// 在任意位置插入
insert(ele, index){
if(index >= 0 && index<=this.count){
const node = new DoubleNode(ele);
let current = this.head;
if(index === 0){
if(this.head === null){
this.head = node;
this.tail = node;
}else{
node.next = this.head;
current.pre = node;
this.head = node;
}
}else if(index === this.count){
current = this.tail;
current.next = node;
node.pre = current;
this.tail = node;
}else{
const previous = this.getElementAt(index - 1);
current = previous.next;
node.next = current;
previous.next = node;
current.pre = node;
node.pre = previous;
}
this.count++;
return true;
}
return false;
}
// 移除某个位置
removeAt(index){
if(index>=0 && index<this.count){
let current = this.head;
if(index === 0){
this.head = current.next;
if(this.count === 1){
this.tail = null;
}else{
this.head.pre = null;
}
}else if(index === this.count-1){
current = this.tail;
this.tail = current.pre;
this.tail.next = null;
}else{
current = this.getElementAt(index-1);
const previous = current.pre;
previous.next = current.next;
current.next.pre = previous;
}
this.count--;
return current.ele;
}
return undefined;
}
}
3.3 循环链表
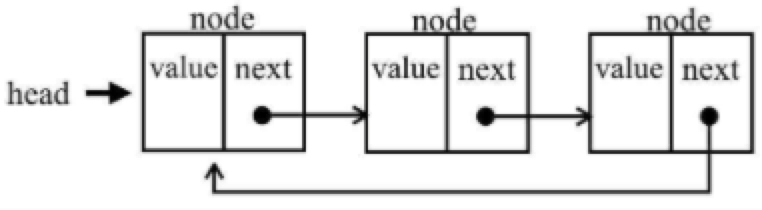
3.3.1 实现
class CircleLinkList extends LinkList{
constructor(){
super();
}
insert(ele, index){
if(index >= 0 && index <= this.count){
const node = new Node(ele);
let current = this.head;
if(index === 0){
if(this.head === null){
this.head = node;
node.next = this.head;
}else{
node.next = this.head;
current = this.getElementAt(this.size());
this.head = node;
current.next = this.head;
}
}else{
const previous = this.getElementAt(index - 1);
node.next = previous.next;
previous.next = node;
}
this.count++;
return true;
}
return false;
}
removeAt(index){
if(index >= 0 && index<this.count){
let current = this.head;
if(index === 0){
if(this.size() === 1){
this.head = null;
}else{
const remove = this.head;
current = this.getElementAt(this.size());
current.next = remove.next;
this.head = this.head.next;
current = remove;
}
}else{
const previous = this.getElementAt(index - 1);
current = previous.next;
previous.next = current.next;
}
this.count--;
return current.ele;
}
return undefined;
}
}
3.5 有序链表
3.5.1 实现
function compare(a, b){
if(a === b) return 0;
return a > b ? -1 : 1;
}
class SortLinkList extends LinkList{
constructor(){
super();
}
insert(ele){
if(this.isEmpty()){
return this.insert(ele, 0);
}
const pos = this.getIndexNextSortEle(ele);
return this.insert(ele, pos);
}
getIndexNextSortEle(ele){
let current = this.head;
let i = 0;
for(; i<this.size() && current;i++){
const comp = this.compare(ele, current.el);
if(comp === -1){
return i;
}
current = current.next;
}
return i;
}
}
4. 集合
集合是一种不允许有重复值的类数组结构,JavaScript中的Set类
// 求并集
Set.prototype.union = function(otherSet){
const unionSet = new Set();
this.values.forEach(e => {
unionSet.add(e);
})
otherSet.values().forEach(e => {
unionSet.add(e)
})
return unionSet;
}
// 求交集
Set.prototype.intersection = function(otherSet){
const intersectionSet = new Set();
this.values.forEach(e => {
if(otherSet.has(e)){
intersectionSet.add(e)
}
})
return intersectionSet;
}
// 求差集
Set.prototype.difference = function(otherSet){
const differenceSet = new Set();
this.values.forEach(e => {
if(!otherSet.has(e)){
differenceSet.add(e)
}
})
return differenceSet;
}
// 求子集
Set.prototype.isSubsetOf = function(otherSet){
if(this.size > otherSet.size) return false;
let isSubset = true;
this.values().every(e => {
if(!otherSet.has(e)){
isSubset = false;
return false;
}
return true;
})
return isSubset;
}
5. 树
二叉查找树
二叉查找树(BST)是二叉树的一种,但是只允许你在左侧节点存储(比父节点)小的值,在右侧节点存储(比父节点)大的值
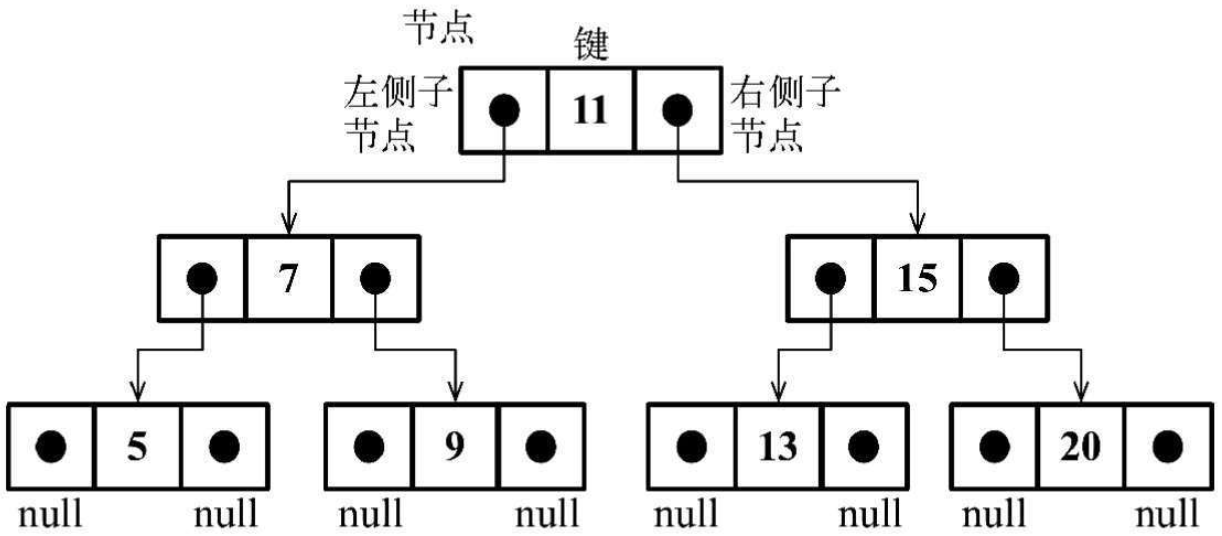
实现
class Node{
constructor(key){
this.key = key;
this.left = null; // 左侧子节点
this.right = null; // 右侧子节点
}
}
class SearchTree{
constructor(){
this.root = null;
}
compareFn(a, b){
if(a > b) return 1;
if(a < b) return -1;
return 0;
}
// 插入新的键
insert(key){
if(this.root === null){
this.root = new Node(key);
}else{
this.insertNode(this.root, key);
}
}
insertNode(node, key){
if(this.compareFn(key, node.key) === -1){ //左小右大
if(node.left === null){ // 左侧空则插入
node.left = new Node(key);
}else{ //左侧有值 找下一个左侧
this.insertNode(node.left, key);
}
}else{
if(node.right === null){
node.right = new Node(key);
}else{
this.insertNode(node.right, key);
}
}
}
// 中序遍历 一个键遍历左边同时遍历右边
middle(callback){
this.middleNode(this.root, callback);
}
middleNode(node, callback){
if(node !== null){
this.middleNode(node.left, callback);
callback(node.key);
this.middleNode(node.right, callback);
}
}
// 先序遍历
pre(callback){
this.preNode(this.root, callback);
}
preNode(node, callback){
if(node !== null){
callback(node.key);
this.preNode(node.left, callback);
this.preNode(node.right, callback);
}
}
// 后序遍历
back(callback){
this.backNode(this.root, callback);
}
backNode(node, callback){
if(node !== null){
this.backNode(node.left, callback);
this.backNode(node.right, callback);
callback(node.key);
}
}
// 获取最小值
min(){
return this.minNode(this.root);
}
minNode(node){
let current = node;
while(current !== null && current.left !== null){
current = current.left;
}
return current;
}
// 获取最大值
max(){
return this.maxNode(this.root);
}
maxNode(node){
let current = node;
while(current !== null && current.right !== null){
current = current.right;
}
return current;
}
// 搜索一个键是否存在
search(key){
return this.searchNode(this.root, key);
}
searchNode(node, key){
if(node === null){
return false;
}
if(this.compareFn(key, node.key) === -1){
return this.searchNode(node.left, key);
}else if(this.compareFn(key, node.key) === 1){
return this.searchNode(node.right, key);
}else{
return true;
}
}
// 移除一个节点
remove(key){
this.root = this.removeNode(this.root, key);
}
removeNode(node, key){
if(node === null) return null;
if(this.compareFn(key, node.key) === -1){
node.left = this.removeNode(node.left, key);
return node;
}else if(this.compareFn(key, node.key) === 1){
node.right = this.removeNode(node.right, key);
return node;
}else{
if(node.left === null && node.right === null){
node = null;
return node;
}
if(node.left === null){
node = node.right;
return node;
}else if(node.right === null){
node = node.left;
return node;
}
const aux = this.minNode(node.right);
node.key = aux.key;
node.right = this.removeNode(node.right, aux.key);
return node;
}
}
}
二叉堆
二叉堆属于特殊的二叉树,它是一棵完全二叉树(尽可能保持所有叶节点都有左右两棵子节点,并且最后一层子节点尽可能是左侧子节点),存在最大二叉堆(所有子节点均小于等于父节点)和最小二叉堆(所有子节点均大于等于父节点)
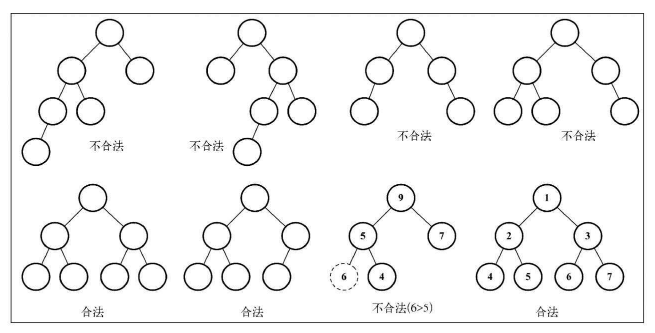
二叉树有两种表示形式,搜索二叉树的动态指针表示形式和数组表示形式
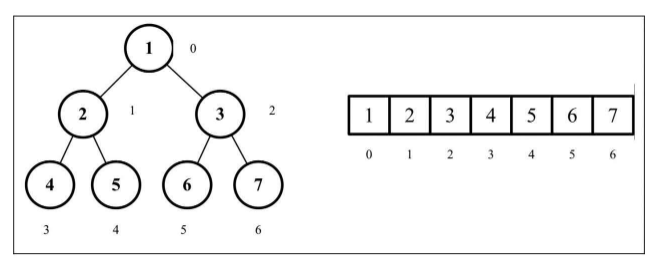
- 左侧子节点获取:2*index + 1 比如通过2获取4的位置
- 右侧子节点获取:2*index + 2 比如通过2获取5的位置
最大二叉堆
实现
class MinHeap{
constructor(){
this.heap = [];
}
compareFn(a, b){
if(a > b) return 1;
if(a < b) return -1;
return 0;
}
// 获取左侧子节点下标
getLeftIndex(index){
return 2*index + 1;
}
// 获取右侧子节点的下表
getRightIndex(index){
return 2*index + 2;
}
// 获取父节点的下表
getParentIndex(index){
if(index === 0) return undefined; //最小值父节点为空
return Math.floor((index-1)/2);
}
// 堆插入值
insert(value){
if(value !== null){
this.heap.push(value);//先插入最后
//根据大小上移
this.shiftUp(this.heap.length - 1);
return true;
}
return false;
}
shiftUp(index){
let parentIndex = this.getParentIndex(index);
while(index > 0 && this.compareFn(this.heap[parentIndex], this.heap[index]) === 1){
[this.heap[parentIndex], this.heap[index]] = [this.heap[index], this.heap[parentIndex]];
index = parentIndex;
parentIndex = this.getParentIndex(index);
}
}
size(){
return this.heap.length;
}
isEmpty(){
return this.size() === 0;
}
findMin(){
this.isEmpty() ? undefined : this.heap[0];
}
// 导出堆中的最小值
extract(){
if(this.isEmpty()) return undefined;
if(this.size() === 1) return this.heap.shift();
const removeValue = this.heap.shift();
this.shiftDown(0); //下移 堆化
return removeValue;
}
shiftDown(index){
let ele = index;
const left = this.getLeftIndex(index);
const right = this.getRightIndex(index);
const size = this.size();
if(left < size && this.compareFn(this.heap[ele], this.heap[left]) === 1){
ele = left;
}
if(right < size && this.compareFn(this.heap[ele], this.heap[right]) === 1){
ele = right;
}
if(index !== ele){
[this.heap[index], this.heap[ele]] = [this.heap[ele], this.heap[index]];
this.shiftDown(ele);
}
}
}
应用示例
堆排序
const arr = [2,6,3,5,4,1,7]
var len;
function buildMaxHeap(arr) { //建堆
len = arr.length;
// [n/2-1]表示的是最后一个有子节点 (本来是n/2(堆从1数起),但是这里arr索引是从0开始,所以-1)
for (var i = Math.floor(len/2)-1; i>=0; i--) {
maxHeapify(arr, i);
}
//对每一个节点(非叶节点),做堆调整
}
function maxHeapify(arr, i) { //堆调整
var left = 2*i+1,
right = 2*i+2,
largest = i; //i为该子树的根节点
if (left < len && arr[left] > arr[largest]) {
largest = left;
}
if (right < len && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) { //即上面的if中有一个生效了
swap(arr, i, largest); //交换最大的为父节点
maxHeapify(arr, largest); //交换后,原值arr[i](往下降了)(索引保存为largest),
//作为根时,子节点可能比它大,因此要继续调整
}
}
function swap(arr, i, j) {
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
function heapSort(arr) {
buildMaxHeap(arr);
for (var i = arr.length-1; i > 0; i--) {
swap(arr, 0, i);
len--;
maxHeapify(arr, 0);
}
return arr;
}
console.log(heapSort(arr))
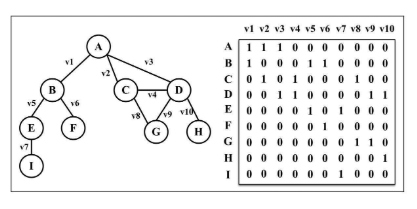
图
邻接矩阵
两个点有连接则为1,无连接则为0,二维数组表示
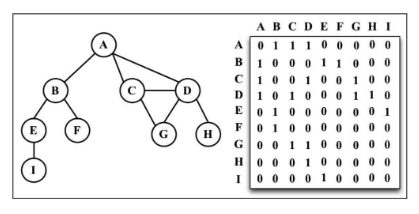
邻接表
只把与自己有连接的写入对象的数组里面
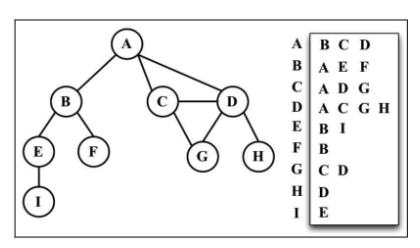
关联矩阵
矩阵的行表示顶点,列表示边,若顶点A是边v1的入射点则arr[A][v1] = 1否则为0