数据结构-线性表提示：正常状态下，顺序表申请的存储容量要大于顺序表的长度。我们看到，上图根本无法体现出各数据之间的逻

算法的基础，永远绕不过去的坎；了解哈常用的数据结构；

分类

一般说来，数据结构分为三个大类

线性表

树结构

图存储结构

下面介绍其中之一线性表：

线性表

概念：全名线性存储结构；

通俗的解释：把所有数据用一根线儿串起来，在存储到物理空间中；

官方解释：将具有“一对一”关系的数据“线性”地存储到物理空间中；

特点：

存储的数据结构往往是可以依次排列的，具备一对一关系的数据就可以使用线性表来存储；

比如：存储类似 {1,3,5,7,9} 这样的数据时，各元素依次排列，每个元素的前面和后边有且仅有一个元素与之相邻（除首元素和尾元素），因此可以使用线性表存储;

存储的数据类型必须一致；否则无法存储

顺序表

概念：将“具有 '一对一' 逻辑关系的数据按照次序连续存储到一整块物理空间上”的存储结构；

如下图：

简单的理解，其实就是数组（方便理解和学习，数组不属于数据结构的范畴）

注意：

由于顺序表结构的底层实现借助的就是数组，因此对于初学者来说，可以把顺序表完全等价为数组，但实则不是这样。数据结构是研究数据存储方式的一门学科，它囊括的都是各种存储结构，而数组只是各种编程语言中的基本数据类型，并不属于数据结构的范畴。

顺序表初始化

顺序表申请的存储容量；
顺序表的长度，也就是表中存储数据元素的个数；

提示：正常状态下，顺序表申请的存储容量要大于顺序表的长度。

方法

都知道一个表是可以进行增删改的；顺序表也不例外；

插入元素

插入方式：
- 插入顺序头
- 表的中间插入
- 作为表的最后一个元素
原理：通过遍历，找到数据元素要插入的位置，然后将要插入的位置元素以及后续的元素整体向后移动位置，将插入的元素放到腾出来问位置上；
删除元素

原理同插入元素；
更改元素

原理：遍历找到目标元素，直接修改元素的值即可；

链表

概念：将“具有 '一对一' 逻辑关系的数据随机存储到一整块物理空间上”的存储结构

例如，使用链表存储 {1,2,3}，数据的物理存储状态如图 1 所示：

我们看到，上图根本无法体现出各数据之间的逻辑关系。对此，链表的解决方案是，每个数据元素在存储时都配备一个指针，用于指向自己的直接后继元素。如下图所示：

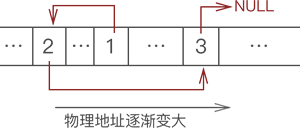
向上图数据元素随机存储，并通过指针表示数据之间逻辑关系的存储结构就是链式存储结构。

链表的节点

从上图可以看到，链表中每个数据的存储都由以下两部分组成：

数据元素本身，其所在的区域称为数据域；
指向直接后继元素的指针，所在的区域称为指针域；

即链表中存储各数据元素的结构如下图所示：

图上所示的结构在链表中称为节点。也就是说，链表实际存储的是一个一个的节点，真正的数据元素包含在这些节点中，如下图所示：

头节点、头指针和首元节点

其实，上图所示的链表结构并不完整。一个完整的链表需要由以下几部分构成：

头指针：一个普通的指针，它的特点是永远指向链表第一个节点的位置。很明显，头指针用于指明链表的位置，便于后期找到链表并使用表中的数据；
节点：链表中的节点又细分为

头节点

首元节点

和其他节点：
- 头节点：其实就是一个不存任何数据的空节点，通常作为链表的第一个节点。对于链表来说，头节点不是必须的，它的作用只是为了方便解决某些实际问题；
- 首元节点：由于头节点（也就是空节点）的缘故，链表中称第一个存有数据的节点为首元节点。首元节点只是对链表中第一个存有数据节点的一个称谓，没有实际意义；
- 其他节点：链表中其他的节点；

因此，一个存储 {1,2,3} 的完整链表结构如下图所示：

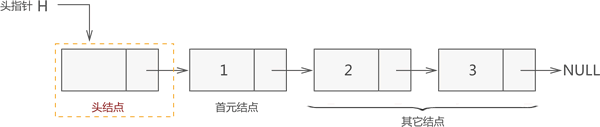
链表初始化

声明一个头指针（如果有必要，可以声明一个头节点）；
创建多个存储数据的节点，在创建的过程中，要随时与其前驱节点建立逻辑关系；

栈和队列

栈

定义：栈是一种只能从表的一端存取数据且遵循 "先进后出" 原则的线性存储结构

特点：

栈只能从表的一端存取数据，另一端是封闭的；

在栈中，无论是存数据，还是读取数据，都必须遵循 *先进后出*的原则；

进栈和出栈

基于栈的结构特点，在实际应用中，通常只会对栈执行以下两种操作：

向栈中添加元素，此过程被称为 进栈（入栈或者压栈）
从栈中取出指定元素，此过程被称为 出栈或者弹栈

栈的具体实现

栈是一种 "特殊" 的线性存储结构，因此栈的具体实现有以下两种方式：

顺序栈：采用顺序存储结构可以模拟栈存储数据的特点，从而实现栈存储结构；------>数组实现
链栈：采用链式存储结构实现栈结构；-------> 链表实现：实际上就是一个只能采用头插法插入（入栈）或删除（出栈）数据的链表

栈的创建（顺序栈）

首先是需要创建一个类

function Stack() {

  *// 各种属性和方法的声明*

}

常见的方法：

push(element):添加一个或是几个新元素到栈顶。

pop():移除栈顶的元素，同时返回被移除元素。

peek():返回栈顶的元素，但并不对栈顶的元素做出任何的修改。

isEmpty():检查栈内是否有元素，如果有返回true，没有返回false。

clear():清除栈里的元素。

size():返回栈的元素个数。

print():打印栈里的元素。

队列

队列是一种先进先出的线性表；从尾部添加新元素，从顶部移除元素，最新添加的元素必须排在队列的末尾；

常见的队列例子：生活中的排队，先排队的就先接受服务，后面的就后接受服务；

特点

队列的两边都是开口，数据是从一端进，一端出；
无论是取数据，还是加数据都是遵循**先进先出**的特点

队列的实现

顺序队列：在顺序表的基础上实现的队列结构；
链队列：在链的基础上实现的队列结构；

队列的创建

常见的方法

enqueue(element):向队列尾部添加一个（或是多个）元素。
dequeue():移除队列的第一个元素，并返回被移除的元素。
front():返回队列的第一个元素——最先被添加的也是最先被移除的元素。队列不做任何变动。
isEmpty():检查队列内是否有元素，如果有返回true，没有返回false。
size():返回队列的长度。
print():打印队列的元素

数据结构-线性表

分类

线性表

分类

顺序表