红黑树原理和算法，超详细介绍（图，内附实现代码）

二叉搜索树

普通的二叉搜索树，如果是一颗平衡的二叉树。

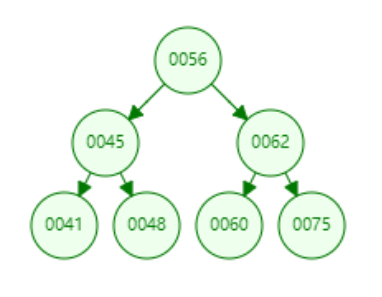
则n个节点查找的时间复杂度为O(log2n),近似折半查找。
如果二叉搜索树完全不平衡，则会退化为一条链表

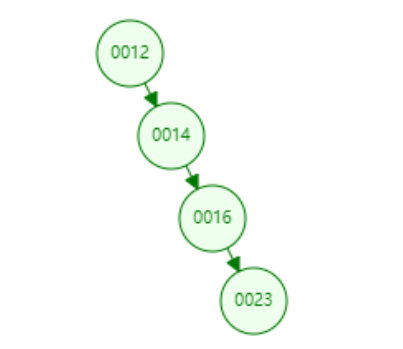
它的时间复杂度为O(n)。
因此为了解决这个问题，出现了avl树(自平衡二叉树)。 嗯，它不重要，不是我要讲的重点。(～￣▽￣)～

avl树

avl树一个高度平衡的二叉树。
它具有一下性质：它的左右子树的高度差绝对值不超过1，且它的左右子树都是一颗平衡二叉树。 avl树追求完全平衡，当插入一个新节点，只要不满足高度差的绝对值小于等于1，就通过旋转来平衡。这种方式，在插入，删除频繁的操作中，反而牺牲了性能。嗯，它也不重要，也不是我要说的重点。ο(=•ω＜=)ρ⌒☆

红黑树

接下来就是我要说的重点啦(✿◡‿◡)。红黑树是一种特殊的avl树。它不追求高度的平衡，它只要求部分平衡，给树的节点增加颜色和规则，达到非严格的平衡。
一颗标准的红黑树，它满足以下性质：
       1.树节点不是黑色就是红色。
       2.根节点是黑色的。
       3.红色节点的子节点必须是黑色。
       4.空叶子节点是黑色的。
       5.从一个节点到叶子节点所有路径包含的黑色节点个数是相同的。
       6.刚插入的节点为红色，即一个节点初始化时为红色。

红黑树的旋转

必要知识点✧
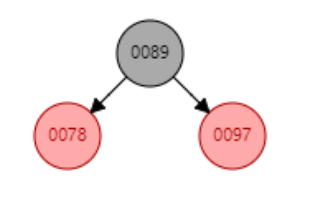
左旋：

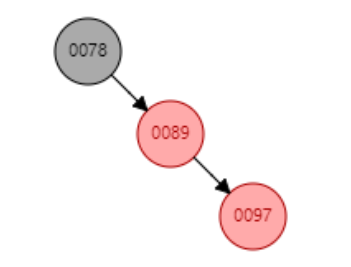
如上图，对0078节点进行左旋 下图 ↓ (其实就是将0078节点变成0089的左节点的意思o‿≖✧)

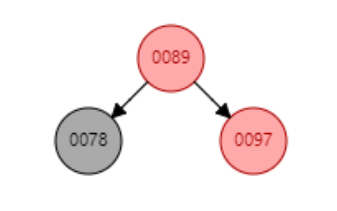
变色↓

=====================================
右旋：

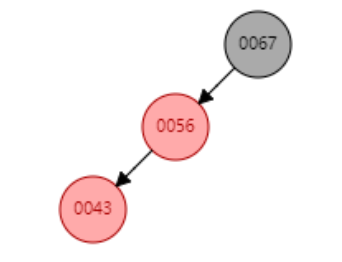
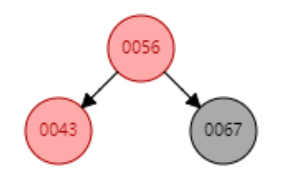
如上图，对0067节点进行右旋 下图↓ (将0067节点变成0056的右节点)

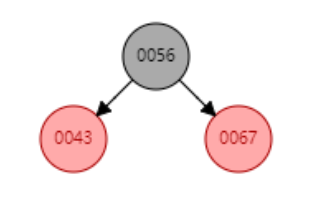
变色↓

红黑树插入时维护规则

新插入的节点存在以下几种可能 ✧：
1.当前插入的节点是根节点直接变色（性质2）。(・ω< )★
if(root==null){
  root=new Node(data);
  root.color=Color.BLACK;
  return true;
}
2.当前插入节点的父节点和叔父节点都是红色节点。父节点，叔父节点，祖父节点变色。
if(uncle!=null&&parent.color==Color.RED&&uncle.color==Color.RED){
  //父节点变色 red->black 该路径下多了一个黑节点
  changeColor(parent);
  //叔叔节点变色red->black 该路径下多了一个黑节点
  changeColor(uncle);
  //祖父节点变色black->red 该路径下少一个黑节点，则到parent和到uncle节点的路径黑节点的个数不变
  changeColor(gParent);
  //下一个可能冲突的节点
  node=gParent;
  continue;
}

图示

  →   

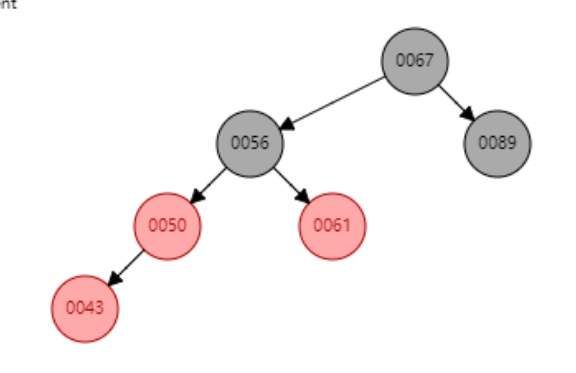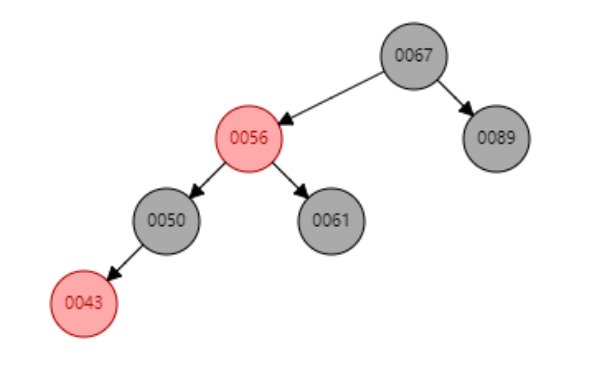
3.红红冲突，父节点为红色，叔父节点黑色，并且当前插入节点是父节点的右节点，父节点是祖父节点的右节点，对祖父节点进行左旋，并变色(・ω< )★

    //旋转核心思想 将红-红冲突往下移，避免往上波及从而影响整棵树
	if((uncle==null||uncle.color==Color.BLACK)&&parent.color==Color.RED){
		//case 2: parent红色节点uncle黑色节点,node为parent的右节点
		if(node==parent.right&&parent==gParent.right){
			//对node的祖父节点进行左旋
			Node<T> left=parent.left;
					
			if(root!=gParent&&gParent.parent.left==gParent){
				gParent.parent.left=parent;
			}else if(root!=gParent){
				gParent.parent.right=parent;
			}else{
				root=parent;
			}
			parent.parent=gParent.parent;
			gParent.parent=parent;
			parent.left=gParent;
			gParent.right=left;
					
			if(left!=null){
				left.parent=gParent;
			}
					
			//更改父节点，祖父节点颜色
			changeColor(parent);//红-->黑
			changeColor(gParent);//黑-->红,可能引起冲突
			//由于现在gPatent的右节点是原来的parent左节点，且parent原来的颜色是红色，则原来parent的左节点颜色是黑色，移动到gParent的右边必不会产生冲突
			//所以新冲突点可能在现在的gParent的左边
			node=gParent.left;
			continue;
		}
	}

图示↓

  →  
 

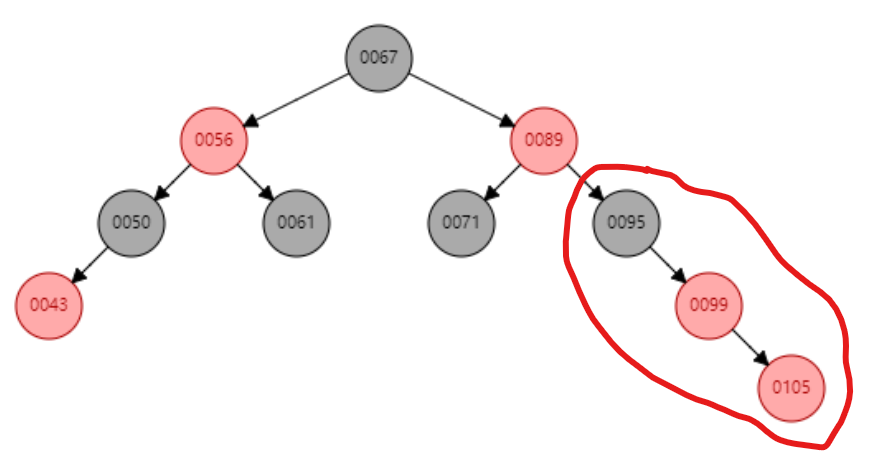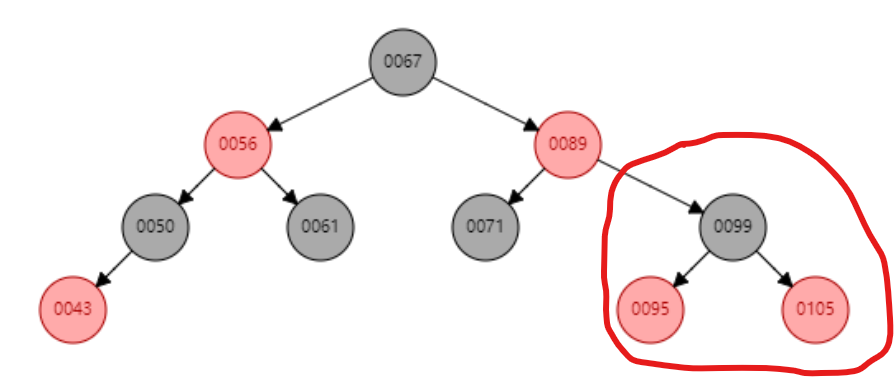
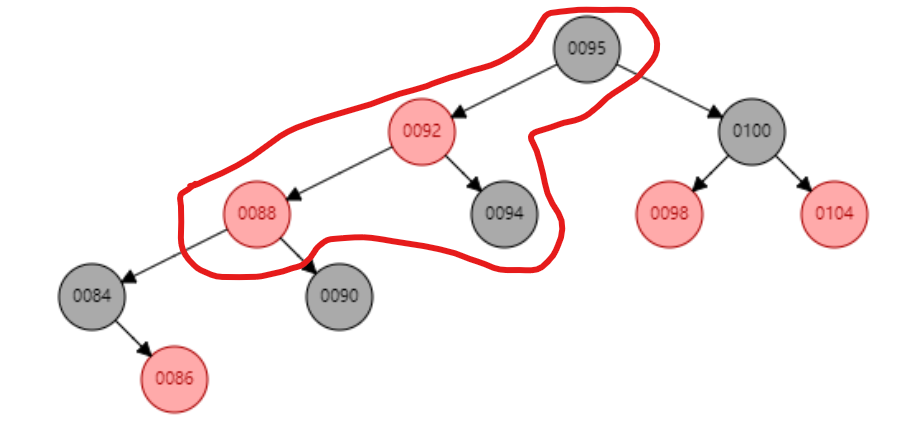
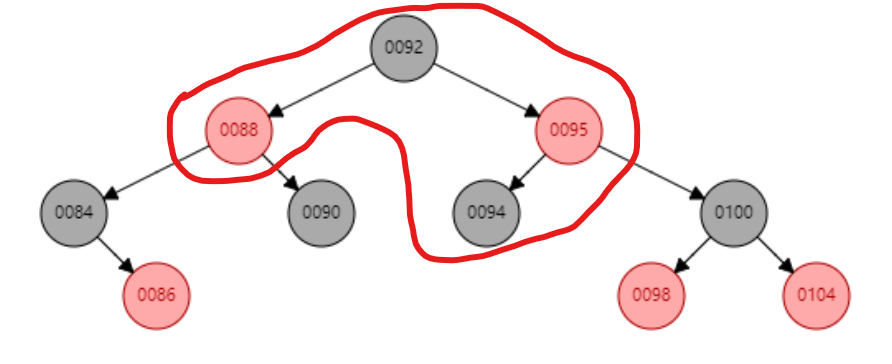
3.红红冲突，父节点为红色，叔父节点黑色，并且当前插入节点是父节点的左节点，父节点是祖父节点的左节点，对祖父节点进行右旋，并变色(・ω< )★

    //旋转核心思想 将红-红冲突往下移，避免往上波及从而影响整棵树
	if((uncle==null||uncle.color==Color.BLACK)&&parent.color==Color.RED){
	    if(node==parent.left&&parent==gParent.left){
			//对node的祖父节点进行右旋
			Node<T> right = parent.right;
			if(gParent!=root){
				if(gParent.parent.left==gParent){
					gParent.parent.left=parent;
				}else{
					gParent.parent.right=parent;
				}
			}else{
				root=parent;
			}
			parent.parent=gParent.parent;
			parent.right=gParent;
			gParent.parent=parent;
			gParent.left=right;
			if(right!=null){
				right.parent=gParent;
			}
			//更改父节点，祖父节点颜色
			changeColor(parent);//红-->黑
			changeColor(gParent);//黑-->红，可能引起新一轮冲突
			//由于现在gPatent的右节点是原来的parent右节点，且parent原来的颜色是红色，则原来parent的右节点颜色是黑色，移动到gParent的左边必不会产生冲突
			//所以新冲突点可能在现在的gParent的右边
			node=gParent.right;
			continue;
		}
	}

图示↓

  →  

满头大汗，终于写完这部分了
 
 
 
以下是本人自己实现的源代码，只实现了添加方法，至于删除的方法来日方长。
RedBlackTree.java

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
/**
 * 红黑树<br>
 * 规则：<br>
 * 1.根节点必须是黑色<br>
 * 2.红色节点的子节点必须是黑色<br>
 * 3.从一个节点到叶子节点的所有路径包含的黑色节点个数相同<br>
 * 4.节点颜色只有红色黑色两种<br>
 * 5.空叶子节点是黑色节点<br>
 * 6.刚插入未确定位置的节点，即初始化一个节点的颜色为红色<br>
 * @author Administrator
 *
 * @param <T>
 */
public class RedBlackTree<T extends Comparable<T>> {
	private Node<T> root;
	public boolean add(T data){
		if(root==null){
			root=new Node<T>(data);
			root.color=Color.BLACK;
			return true;
		}
		Node<T> node=new Node<>(data);
		Node<T> currNode=root;
		//寻找插入位置
		A:while(true){
			if(currNode.data.compareTo(node.data)<=0){
				if(currNode.right!=null){
					currNode=currNode.right;
				}else{
					currNode.right=node;
					node.parent=currNode;
					break A;
				}
			}else{
				if(currNode.left!=null){
					currNode=currNode.left;
				}else{
					currNode.left=node;
					node.parent=currNode;
					break A;
				}
			}
		}
		//判断是否是标准红-黑树
		B:while(true){
			if(node==null){
				break B;
			}
			//不是新插入的节点，经过变色，旋转，找到下一个可能冲突的节点
			if(node.color==Color.BLACK){
				break B;
			}
			if(root==node){
				//如果当前节点是根节点且是红色，直接变换颜色
				if(root.color==Color.RED){
					changeColor(root);
				}
				break B;
			}
			Node<T> parent = node.parent;
			//如果当前插入节点的父节点是红色，红红冲突，变换父节点颜色
			if(parent==root){
				if(root.color==Color.RED){
					changeColor(root);
				}
				break B;
			}
			//父节点颜色是黑色，没有违反红黑树规则
			if(parent.color==Color.BLACK){
				break B;
			}
			Node<T> uncle=null;
			Node<T> gParent=parent.parent;
			if(parent==gParent.left){
				uncle=gParent.right;
			}else{
				uncle=gParent.left;
			}
			//case 1: uncle和parent都是红色节点
			if(uncle!=null&&parent.color==Color.RED&&uncle.color==Color.RED){
				//父节点变色 red->black 该路径下多了一个黑节点
				changeColor(parent);
				//叔叔节点变色red->black 该路径下多了一个黑节点
				changeColor(uncle);
				//祖父节点变色black->red 该路径下少一个黑节点，则到parent和到uncle节点的路径黑节点的个数不变
				changeColor(gParent);
				//下一个可能冲突的节点
				node=gParent;
				continue;
			}
			//旋转核心思想 将红-红冲突往下移，避免往上波及从而影响整棵树
			if((uncle==null||uncle.color==Color.BLACK)&&parent.color==Color.RED){
				//case 2: parent红色节点uncle黑色节点,node为parent的右节点
				if(node==parent.right&&parent==gParent.right){
					//对node的祖父节点进行左旋
					Node<T> left=parent.left;
					
					if(root!=gParent&&gParent.parent.left==gParent){
						gParent.parent.left=parent;
					}else if(root!=gParent){
						gParent.parent.right=parent;
					}else{
						root=parent;
					}
					parent.parent=gParent.parent;
					gParent.parent=parent;
					parent.left=gParent;
					gParent.right=left;
					
					if(left!=null){
						left.parent=gParent;
					}
					
					//更改父节点，祖父节点颜色
					changeColor(parent);//红-->黑
					changeColor(gParent);//黑-->红,可能引起冲突
					//由于现在gPatent的右节点是原来的parent左节点，且parent原来的颜色是红色，则原来parent的左节点颜色是黑色，移动到gParent的右边必不会产生冲突
					//所以新冲突点可能在现在的gParent的左边
					node=gParent.left;
					continue;
				}
				//case 3: parent红色节点uncle黑色节点,node为parent的左节点
				else if(node==parent.left&&parent==gParent.left){
					//对node的祖父节点进行右旋
					Node<T> right = parent.right;
					if(gParent!=root){
						if(gParent.parent.left==gParent){
							gParent.parent.left=parent;
						}else{
							gParent.parent.right=parent;
						}
					}else{
						root=parent;
					}
					parent.parent=gParent.parent;
					parent.right=gParent;
					gParent.parent=parent;
					gParent.left=right;
					if(right!=null){
						right.parent=gParent;
					}
					//更改父节点，祖父节点颜色
					changeColor(parent);//红-->黑
					changeColor(gParent);//黑-->红，可能引起新一轮冲突
					//由于现在gPatent的右节点是原来的parent右节点，且parent原来的颜色是红色，则原来parent的右节点颜色是黑色，移动到gParent的左边必不会产生冲突
					//所以新冲突点可能在现在的gParent的右边
					node=gParent.right;
					continue;
				}
			}
		}
		cengciBinli();
		return true;
	}
	private void changeColor(Node<T> node){
		if(node.color==Color.RED){
			node.color=Color.BLACK;
		}else{
			node.color=Color.RED;
		}
	}
	/**
	 * 非递归 中序遍历
	 * @param node
	 */
	public void midPrintNode(Node<T> node){
		Stack<Node<T>> stack=new Stack<>();
		while(node!=null||!stack.isEmpty()){
			while(node!=null||!stack.isEmpty()){
				while(node!=null){
					stack.push(node);
					node=node.left;
				}
				if(!stack.isEmpty()){
					Node<T> pop = stack.pop();
					System.out.print("[data:"+pop.data+",color:"+pop.color.name()+"]  ");
					node=pop.right;
				}
			}
		}
		
	}
	public void cengciBinli(){
		System.out.println("\n--------------层次遍历----------------");
		//定义一个节点队列
		Queue<Node<T>> queue = new LinkedList<>();
		Queue<Node<T>> sq=new LinkedList<>();
		queue.add(this.root);
		A:while(true){
			while(queue.size()>0){
				
				Node<T> node = queue.poll();
				if(node == null){
					break A;
				}
				System.out.print("[data:"+node.data+",color:"+node.color.name()+",parent:"+(node.parent!=null?node.parent.data:"")+"]   ");
				if(node.left != null){
					sq.add(node.left);
				}
				if(node.right != null){
					sq.add(node.right);
				}
			}
			if(sq.size()==0){
				break A;
			}
			queue.addAll(sq);
			sq.clear();
			System.out.println();
		}
	}
	public Node<T> getRoot(){
		return this.root;
	}
	private class Node<T extends Comparable<T>>{
		private T data;
		private Node<T> left;
		private Node<T> right;
		private Node<T> parent;
		private Color color;
		public Node(T data){
			this.data=data;
			this.color=Color.RED;
		}
		public Node(){
			
		}
	}
	private enum Color{
		RED,
		BLACK;
	}
}