回形取数

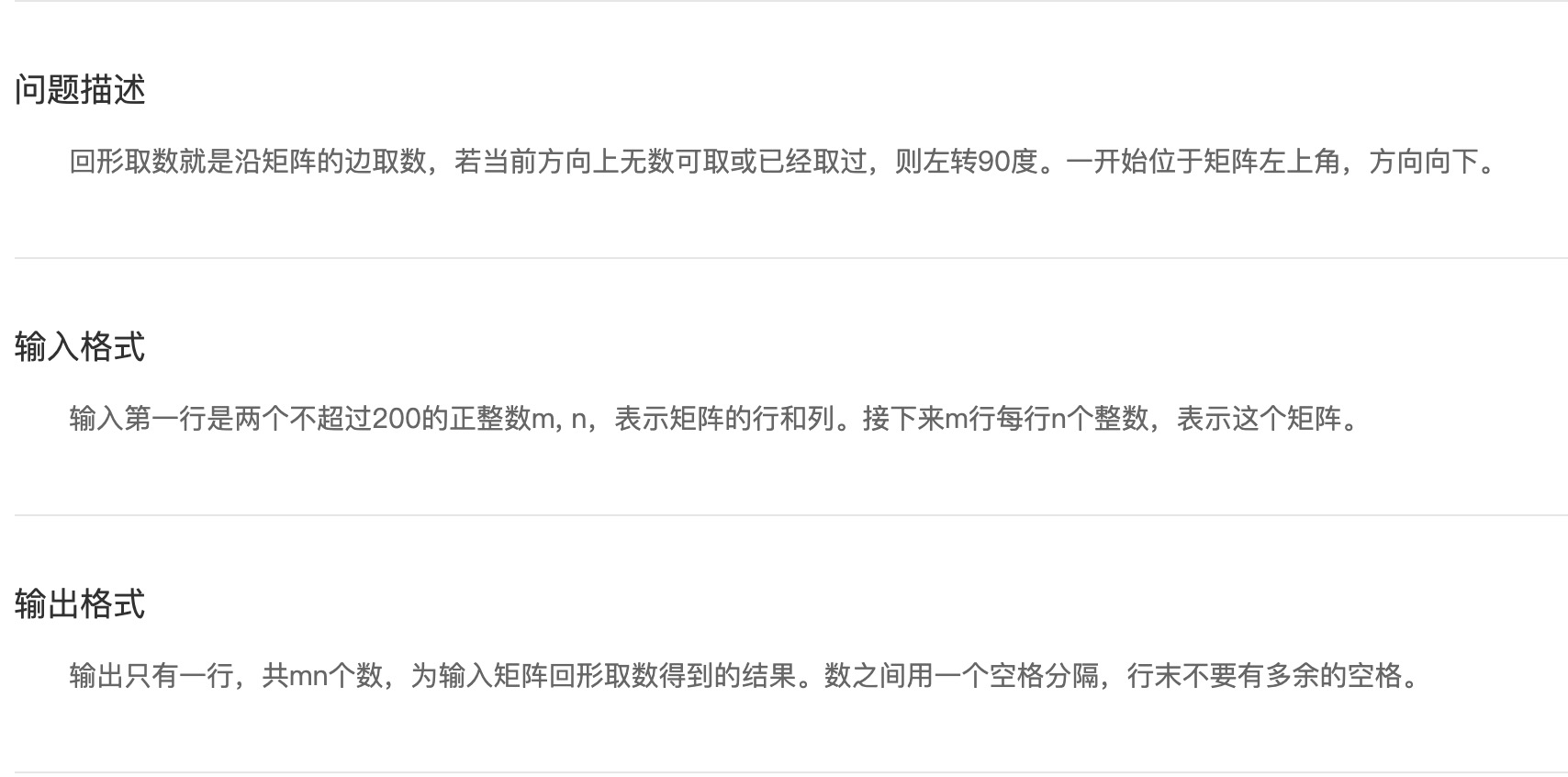
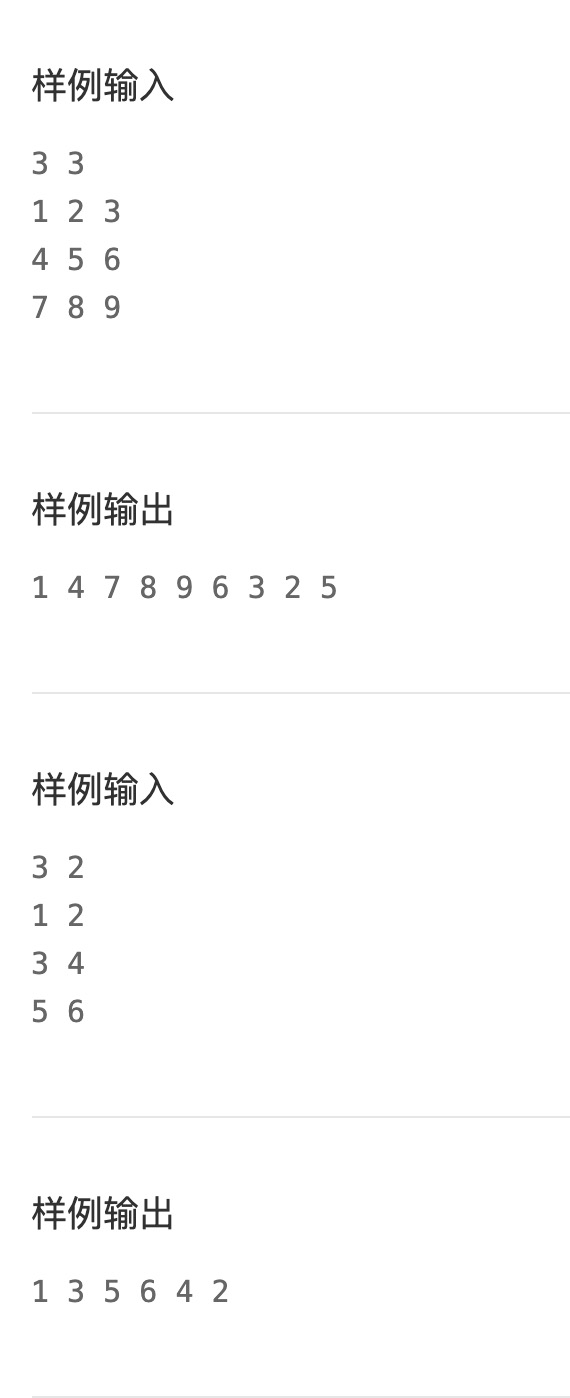
解析: 看过其他人的解题方式，发现大家都是给定多个判断条件来判断边界和什么时间转向。我觉得这样的话解题步骤就很多了，而且判断条件一多起来就容易写错。

一看到题目中有矩阵，并且要输入m行，n列，我第一反应就是这题应该和二维数组有关。 根据题目题意画了下面这个草图：

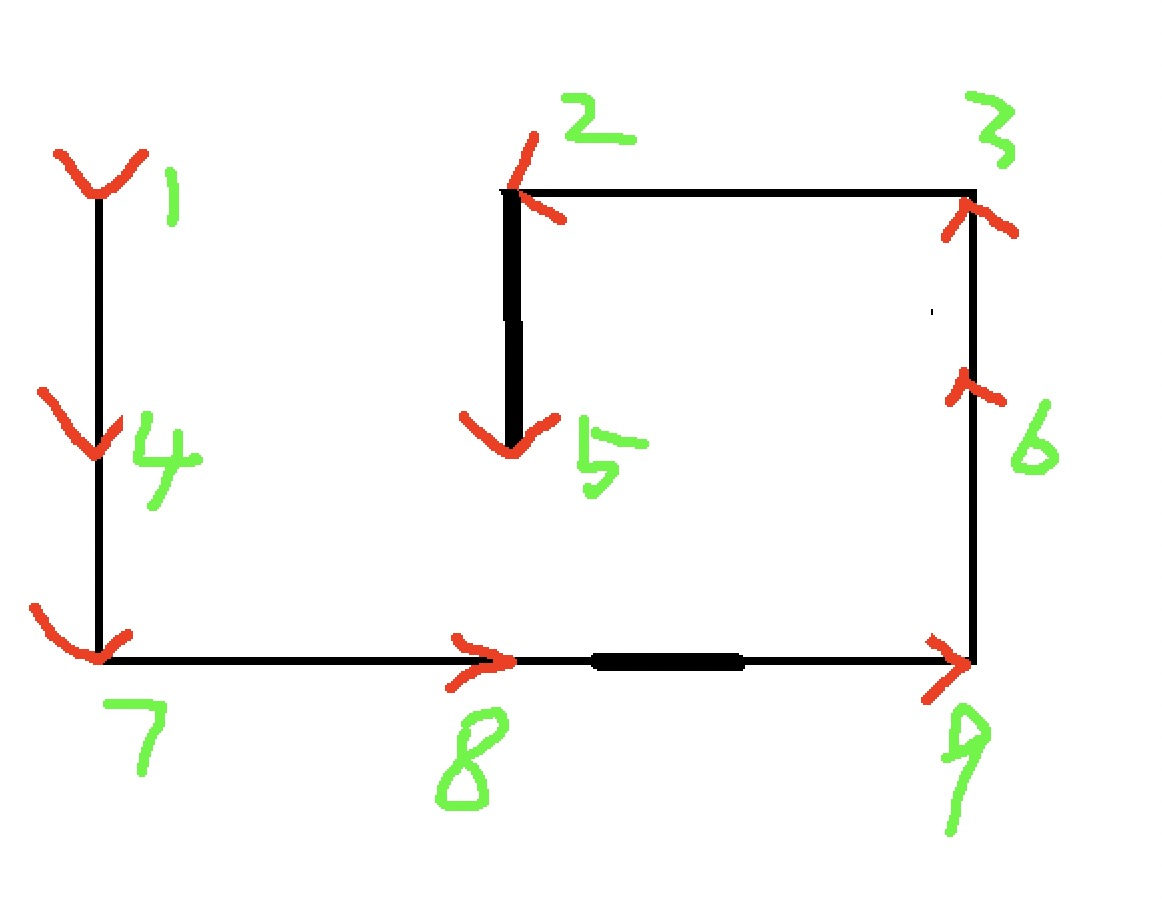
这是一个 3*3 的草图。其实数据3*3的这个效果还不是很明显，弄个5*5的就可以看出很明显的规律了。

题目要我们沿矩阵的边取数，并且碰到边界或者已经取过的数就左转90°，也就是逆时针的顺序取数字。进一步理解就是每次取的数都是每行开头和结尾的数，以及每列的开头和结尾的数。顺序就是上面那张图中的:每行最左边的数(从首行到末尾行)->每列最末尾的数(从首列到末尾列)->每行最右边的数(从末尾行到首行)->每列开头的数(从末尾列到首列)。

按照这种思路的话我们只要把关注点放在二维数组的行和列的变化上面就行了。取"左下右上"四个方向的数据时用了4个for循环去实现。

package _3_5_test;

import java.util.Scanner;

/*回形取数
 * 1   2  3  4  5
 * 6   7  8  9  10
 * 11 12 13 14  15
 * 16 17 18 19  20
 * 
 * 规律，每次取的数都是每行首尾的数和每列首尾的数
 * 取数顺序：每行的开头数字(从首行到末尾行)、中间列的末尾数字(从前列到后列)、
 * 		    每行的末尾数字(从末尾行到首行)、中间列的开头数字(从后列到前列)
 * 
 * */
public class Fifty {

	public static void main(String[] args) {
		// TODO Auto-generated method stub

		Scanner scanner = new Scanner(System.in);

		// 行数
		int m = scanner.nextInt();
		// 列数
		int n = scanner.nextInt();

		// 按顺序存放整个矩阵中的数字
		int num[][] = new int[m][n];

		// 存放回型取数后最终的结果
		int result[] = new int[m * n];
		// 用于result[]的下标
		int count = 0;

		// 将矩形中的数字存入二维数组中
		for (int i = 0; i < m; i++) {
			for (int j = 0; j < n; j++) {
				num[i][j] = scanner.nextInt();
			}
		}

//		l是每次取一圈数据时的起始行
		int l = 0;
//		h是每次取一圈数据时的起始列
		int h = 0;
//		以result[]的下标为结束条件，如果result[]装满了就结束程序
		loop: while (count < m * n) {
			// 取出行首的数字，从首行到末尾行
			// 行变化，列不变
			for (int i = l; i <= m - 1 - l; i++) {
				if (count >= m * n) {
					break loop;
				}
				result[count] = num[i][h];
				count++;
			}

			// 取出中间列末尾的数字，从前列到后列
			// 行不变，一直是最后一行，列变化，去掉行的开头和结尾
			for (int i = h + 1; i < n - 1 - h; i++) {
				if (count >= m * n) {
					break loop;
				}
				result[count] = num[m - 1 - l][i];
				count++;
			}

			// 取出行尾的数字，从末尾行到首行
			// 行变化，列不变
			for (int i = m - 1 - l; i >= l; i--) {
				if (count >= m * n) {
					break loop;
				}
				result[count] = num[i][n - 1 - h];
				count++;
			}

			// 取出中间列首位的数字，从后列到前列
			// 行不变，一直是第一行，列变化，去掉行的开头和结尾
			for (int i = n - 2 - h; i >= 1 + h; i--) {
				if (count >= m * n) {
					break loop;
				}
				result[count] = num[l][i];
				count++;
			}
			l++;
			h++;
		}

//		输出最终的结果
		for (int i = 0; i < result.length; i++) {
			System.out.print(result[i] + " ");
		}

	}

}