LeetCode - 001 - 46.Permutations - 1314. Matrix Block Sum

Date: 20200323

46.Permutations

Given a collection of distinct integers, return all possible permutations.

基本信息

Difficulty: Medium

v0.1.0

一开始没好好审题写了一个三重循环，结果发现collection of integers的个数的不定的。好几个月没写c++还是好不习惯。

看清楚题目意思以后第一反应就是recursion。

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> result;
        vector<int> s;
        
        permute_recursive(s, nums, result);
        
        return result;
        
    }
    
    void permute_recursive(vector<int> selected, vector<int> not_selected, vector<vector<int>>& result) {
        if (not_selected.empty()) {
            result.push_back(selected);
        } else {
            for (int i = 0; i < not_selected.size(); i++) {
                vector<int> new_selected = selected;
                new_selected.push_back(not_selected[i]);
                vector<int> new_not_selected = not_selected;
                new_not_selected.erase(new_not_selected.begin() + i);
                permute_recursive(new_selected, new_not_selected, result);
            }
        }
    }
    
    
};

submission

Runtime: 20 ms, faster than 9.84% of C++ online submissions for Permutations. Memory Usage: 8.6 MB, less than 100.00% of C++ online submissions for Permutations.

反思

看了一下别人的代码，发现即使都是同样的思路，中间操作vector的方式不同对效率的影响还蛮大的。

v0.2.0 swapping

FS solution with graph illustration

感觉这个discussion post因为有图所以讲得比较清楚。

#include<iostream>
using namespace std;

class Solution {
public:
    vector<vector<int>> result;
    int size;
    
    vector<vector<int>> permute(vector<int>& nums) {
        int index = 0;
        size = nums.size();
        
        swap(nums, index);
        return result;
    }
    
    void swap(vector<int> nums, int index) {
        if (index == size) {
            result.push_back(nums);
        } else {
            for (int i = index; i < size; i++) {
                vector<int> new_num = nums;
                int tmp = new_num[index];
                new_num[index] = new_num[i];
                new_num[i] = tmp;
                swap(new_num, index+1);
            }
        }
    }
};

submission

Runtime: 16 ms, faster than 18.09% of C++ online submissions for Permutations. Memory Usage: 7.9 MB, less than 100.00% of C++ online submissions for Permutations.

反思

一开始把result.push_back卸载了swap的for loop里面，结果result出现了重复的结果。之后意识到其实应该是swap到最后一层再push_back。

运行时间比之前稍微快了一点。

1314. Matrix Block Sum

Given a m * n matrix mat and an integer K, return a matrix answer where each answer[i][j] is the sum of all elements mat[r][c] for i - K <= r <= i + K, j - K <= c <= j + K, and (r, c) is a valid position in the matrix.

基本信息

Difficulty: Medium

v0.1.0

这个下标实在是太麻烦了，来来回回改了很久。动态规划还是不太熟练。

基本思路就是mat[r][c] for i - K <= r <= i + K, j - K <= c <= j + K实际上是一个中心在(i,j)变长为2K+1的正方形，由于边界的问题，最后可能实际是个矩形。

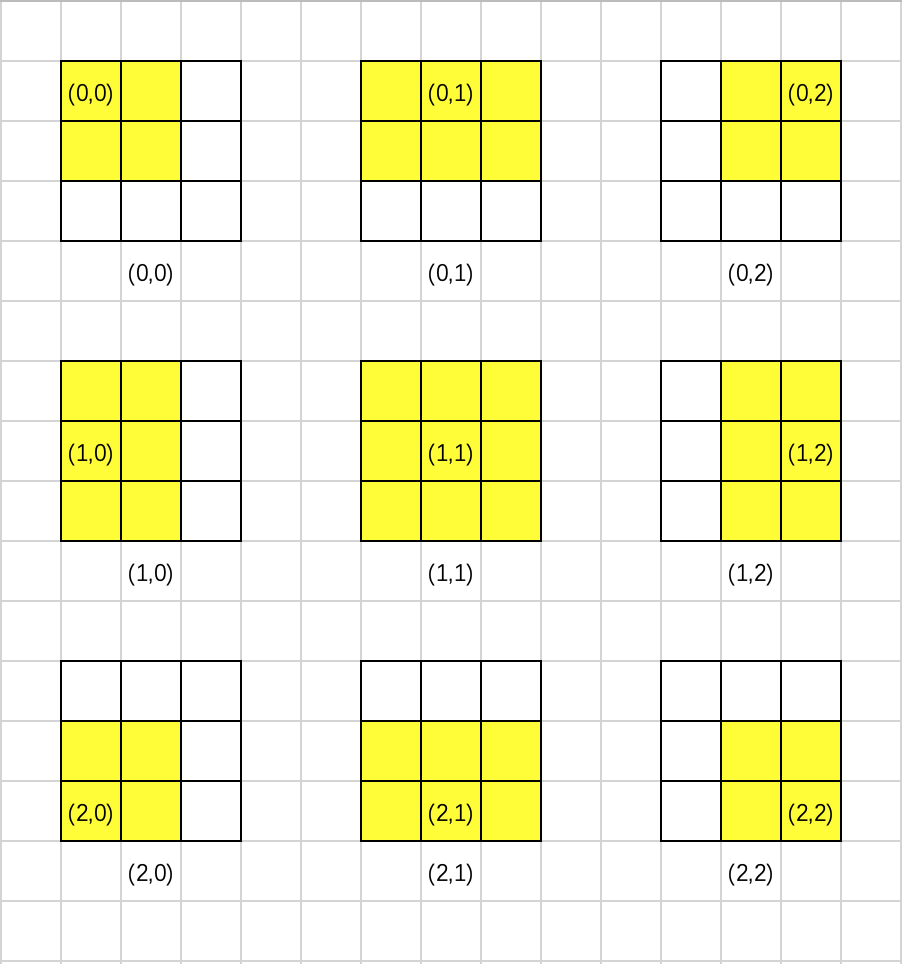
将问题转换一下，实际上就是(i+K, j+K)到(0,0)的矩形内值的和剪去多余的矩形。

也就是减掉下图蓝色部分。

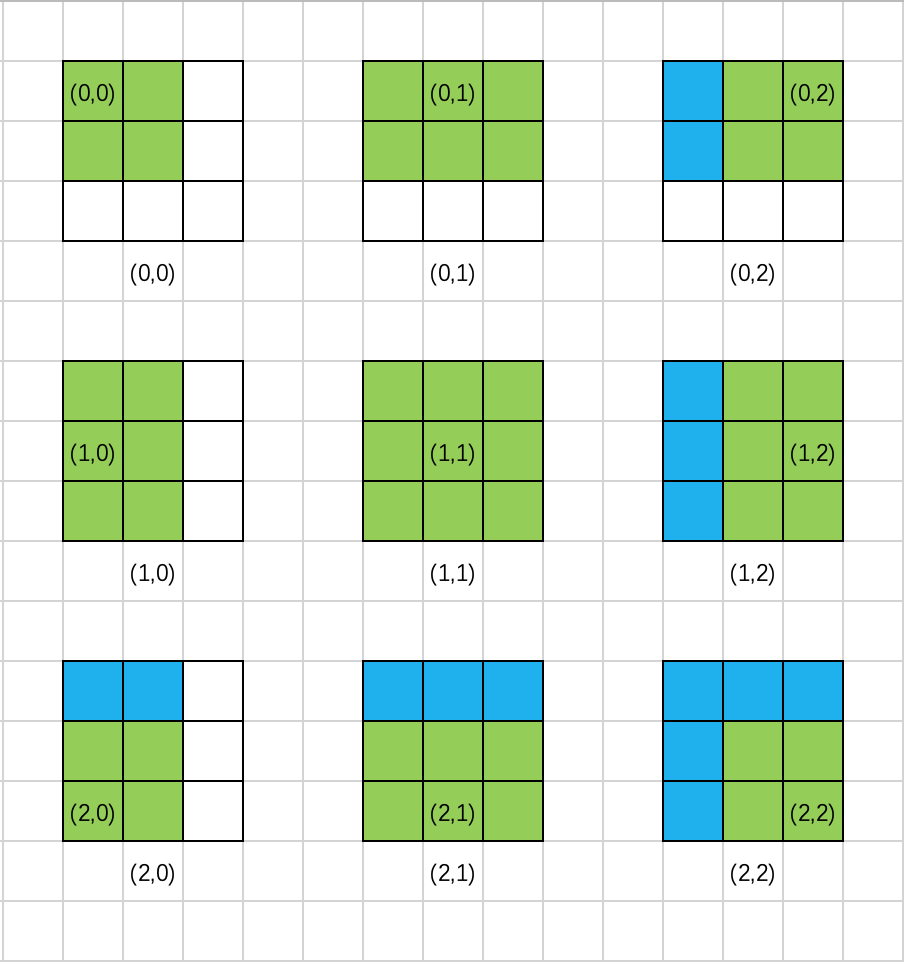
正好昨天刚在一位数组上用到过prefix_sum，所以马上想到可以利用这个避免重复计算。 prefix_sum这个二维数组中， prefex_sum[i][j]代表以(0,0)和(i,j)为对角的矩形内数值的和。

这样answer[2][2]实际上就是prefix_sum[2][2] - prefix_sum[0][2] - prefix_sum[2][0] + prefix_sum[0][0]。（最后要加是因为(0,0)被减去了两次）。

剩下的就是判断i+K, j+K, i-K, j-K有没有超过范围，分情况讨论。

#include<iostream>
using namespace std;

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int K) {
        vector<vector<int>> prefix_sum = prefixSum(mat);
        vector<vector<int>> answer = prefix_sum;
        
        for (int i = 0; i < mat.size(); i++) {
            for (int j = 0; j < mat[0].size(); j++) {
                int upper_i = ((i+K) >= mat.size()) ? (mat.size()-1) : (i+K);
                int upper_j = ((j+K) >= mat[0].size()) ? (mat[0].size()-1) : (j+K);
                
                int lower_i = ((i-K) <= 0 ) ? 0 : (i-K);
                int lower_j = ((j-K) <= 0 ) ? 0 : (j-K);
                
                
                answer[i][j] = prefix_sum[upper_i][upper_j] - ((lower_i == 0) ? 0 : prefix_sum[lower_i-1][upper_j]) - ((lower_j == 0) ? 0 : prefix_sum[upper_i][lower_j-1]) + ((lower_i == 0) || (lower_j == 0)  ? 0 : prefix_sum[lower_i-1][lower_j-1]);
            }
        }
    
        
        return answer;
        
    }
    
    vector<vector<int>> prefixSum(vector<vector<int>>& mat) {
        vector<vector<int>> prefix_sum = mat;
        
        for (int i = 0; i < mat.size(); i++) {
            int sum = 0;
            for (int j = 0; j < mat[0].size(); j++) {
                sum = sum + mat[i][j];
                if (i > 0) {
                    prefix_sum[i][j] = sum + prefix_sum[i-1][j];
                } else {
                    prefix_sum[i][j] = sum;   
                }
            }
        }
        
        return prefix_sum;
        
        
    }
    
};

submission

Runtime: 28 ms, faster than 64.38% of C++ online submissions for Matrix Block Sum. Memory Usage: 9.1 MB, less than 100.00% of C++ online submissions for Matrix Block Sum.

反思

完全自己做出来的，submission的结果我也挺满意。

然后我去看了一下submission部分。有个人post了一个一行代码的python version，可怕。 Python one-line solution

C++ prefix DP matrix O(m*n) 这个思路和我是一样的，不过感觉用max和min来判断coordinates是不是valid好像更直观一点？我偷了个懒都用三元运算判断了写在了一行，就可读性来说会差一点。

过段时间我自己看大概也得皱着眉头研究一会儿。