很多故事都有个前言
一些常见的算法题都可以用递归解决,如果你看过很多leetcode上的题目你就知道了。熟练掌握了递归你也能像别人那样直接几行代码很帅的解决了这个算法题。
常见教科书式的递归介绍
我们在大学里甚至毕业后看的一些数据结构或者算法题里都有递归的介绍,通常会用阶乘介绍递归。如下
假设我们用递归来算阶乘 f(n)
f = n =>
n === 1 ? 1
: n * f(n-1)
f 里面用到了 f,怎么理解呢?很简单,把式子展开即可:
f(6)
=> 6 * f(5)
=> 6 * (5 * f(4))
=> 6 * (5 * (4 * f(3)))
=> 6 * (5 * (4 * (3 * f(2))))
=> 6 * (5 * (4 * (3 * (2 * f(1)))))
=> 6 * (5 * (4 * (3 * (2 * 1))))
=> 6 * (5 * (4 * (3 * 2)))
=> 6 * (5 * (4 * 6))
=> 6 * (5 * 24)
=> 6 * 120
=> 720
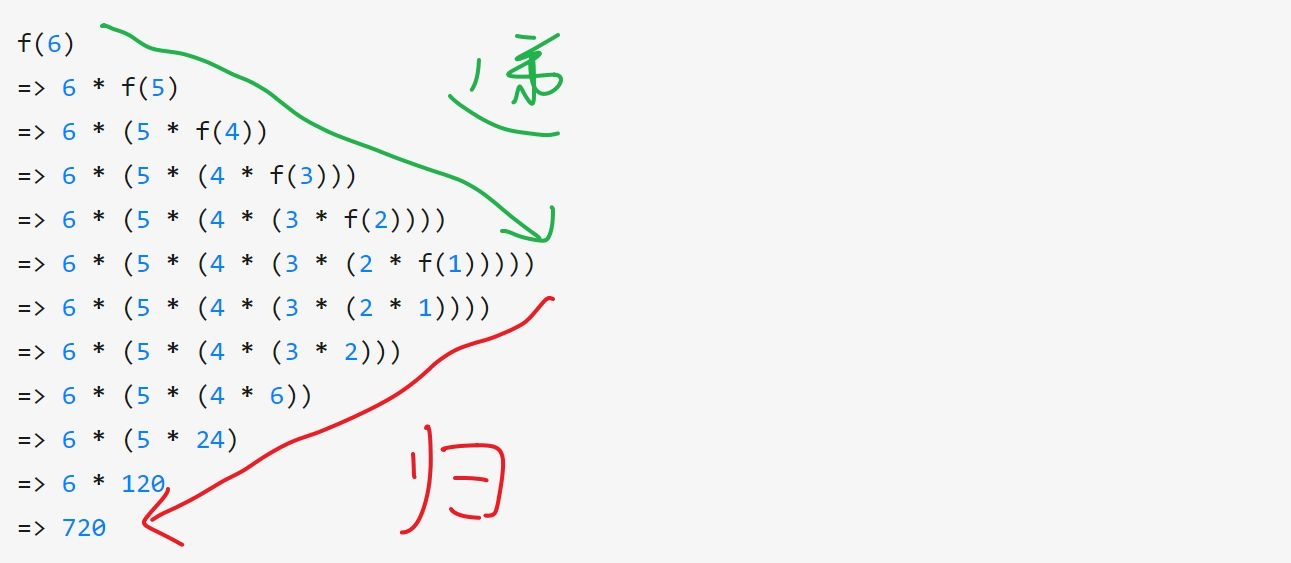
先递进,再回归——这就是「递归」。到这里是不是对这个概念很熟悉了。
那么递归到底能解决那些算法题呢?
Leetcode 104. 二叉树的最大深度 Leetcode 24. 两两交换链表中的节点 Leetcode 110. 平衡二叉树 ......等等
递归的套路
套路一:不要纠结递归的整个过程。
既然递归是一个反复调用自身的过程,这就说明它每一级的功能都是一样的,因此我们只需要关注一级递归的解决过程即可。
套路二:这个主函数是做什么的。
套路三:找到整个递归的终止条件。
套路四:找返回值:应该给上一级返回什么信息。
套路五:我们精简后的一级递归是用来做什么的。
既然找到攻略了我们下面实践下
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例: 给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
- 按照上面的套路我们先构造主函数
- (NSInteger)maxDepthOfTree:(DSTreeNode *)root
- 找整个递归的终止条件:递归应该在什么时候结束? 树为空的时候,此时树的深度为0,递归就结束了。
if (root == nil)
{
return 0;
}
-
找返回值:应该给上一级返回什么? 当前节点的最大深度
-
本级递归应该做什么:在这一级递归中,要做什么?
上述找返回值以及本级递归做什么就是如下操作:
maxDepth(root) = max(maxDepth(root.left), maxDepth(root.right)) + 1
那么综合下这题的解题过程如下:
- (NSInteger)maxDepthOfTree:(DSTreeNode *)root
{
//1
if (root == nil)
{
return 0;
}
//2
else
{
NSInteger left_height = [self maxDepthOfTree:root.leftChild];
NSInteger right_height = [self maxDepthOfTree:root.rightChild];
return MAX(left_height, right_height)+1;
}
}
看到这里是不是发现原来如此,按照这个套路向里面套代码就行了。
总结
数据结构的基本存储方式就是链式和顺序两种,基本操作就是增删查改,遍历方式无非迭代和递归。所以掌握递归还是比较重要的。