一、数组本质
- 数组的本质是把数据存储在计算机内存管理器开辟的连续内存地址对应的位置
- 所以数组的随机访问时间复杂度为O(1),搜索元素的时间复杂度为O(n)
- 插入删除元素由于平均需要移动半个数组的元素,平均时间复杂度为O(n)
二、链表本质
- 链表的本质是每个元素靠指针指向其相邻元素,随机访问需要遍历整个链表
- 访问和搜索的时间复杂度为O(n)
- 插入删除元素只需要处理相邻元素的指针指向关系,所以插入和删除的时间复杂度为O(1)
三、跳表本质
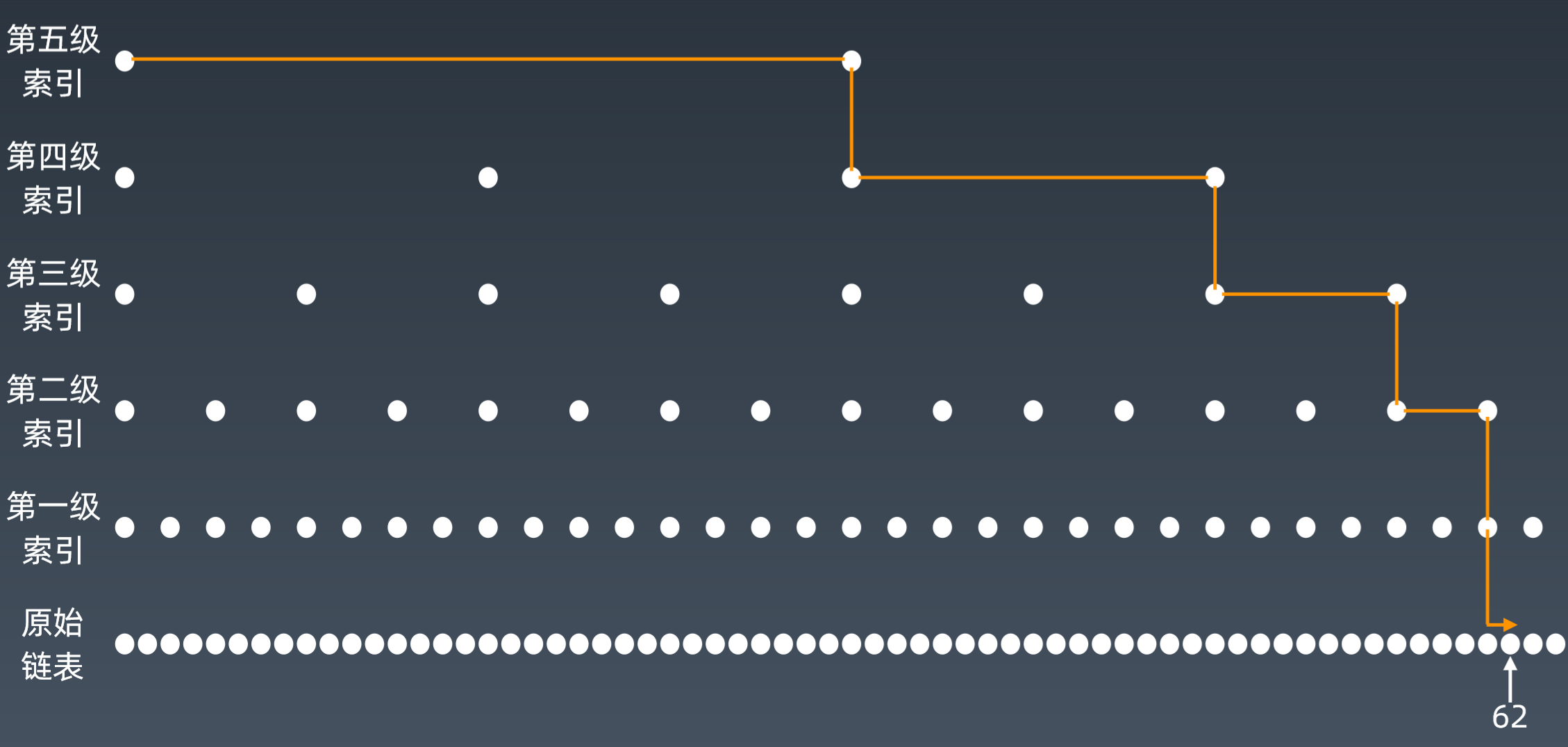
- 跳表的本质是在链表的基础上进行升维,加入多级索引,每级索引不再是跳向相邻元素,而是跳跃 2^k 个元素
- 其底层实现有多种方式,有BST二叉搜索树、AVL平衡二叉树等
- 故其访问和搜索的时间复杂度为O(logn)
- 插入和删除元素的时间复杂度也是O(logn)
- redis 的sorted set的底层实现就是跳表