博弈论系列之耶鲁公开课学习（一）：导论-五个入门结论博弈论的介绍，一般都是从某一种博弈开始，对博弈的过程进行分析，从而得

博弈论的介绍，一般都是从某一种博弈开始，对博弈的过程进行分析，从而得到结论。所以我们就直接上博弈！

成绩博弈

博弈如下，我和我的同桌进行成绩博弈，均只能选择两种策略 $\alpha$ 或者 $\beta$ 。同时，我们只能独自选择策略，无法知道别人的选择。如果我和他同时选择了策略 $\alpha$ ，则我和他的成绩为B-。如果我和他同时选择了策略 $\beta$ ，则我和他的成绩为B+。如果我选择了 $\alpha$ ，他选择了 $\beta$ ，则我得A，他得C。反之亦然。我们可以将该博弈用表格的形式展现如下：

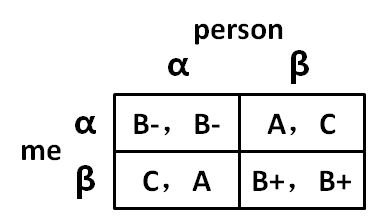
其中表格的左侧为我的策略选择。表格内逗号前面为我的成绩，后面为我同桌的成绩。

现在，我们对每种情况进行逐一分析，为了分析方便，我们可以将成绩都转换为数字，比较方便。

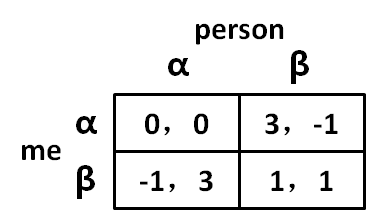
第一种情况，我的同桌选择了策略 $\alpha$ ，那么我选择策略 $\alpha$ 的时候，我的成绩是B-，我选择策略 $\beta$ 时，我的成绩是C。 $0>-1$ ，即我应该选择策略 $\alpha$ 。

第二种情况，我的同桌选择了策略 $\beta$ ，那么我选择策略 $\alpha$ 的时候，我的成绩是A，我选择策略 $\beta$ 时，我的成绩是B+。 $3>1$ ，即我应该选择策略 $\alpha$ 。

这里我们发现，任何情况下，策略 $\alpha$ 的收益均优于策略 $\beta$ 。所以 $\alpha$ 相对于 $\beta$ ，称作严格优势策略（Strictly Dominant Strategy）。

结论一：永远选择严格优势策略，因为在每次博弈都得到更好的收益。

和这个博弈相似的最经典的博弈就是囚徒困境。当每个人都选择了对于自己最优的策略，反而是整体的效果变差（B-,B-差于B+,B+）。也就是经济学115中的帕累托效率(Pareto inefficient)。注：简单来说就是在现有状态下，不存在一个方法，使得在提高一个人的收益时，不降低其他所有人的收益，即不存在帕累托改进。

结论二：理性选择将导致次优结果。

那么如果我和同桌进行沟通协商，是否能扭转结果呢？答案是否定的。因为不具有强制性，即使我和同桌沟通了都选 $\beta$ ，在提交策略的时候，我依然会选择 $\alpha$ ，因为这样我的收益会更高。当然，这里收益是不考虑其他因素在内，比如我的社会信誉、我的人生安全等等。在真实情况中，这些都会算进我的收益中，情况就不一样了。所以黑手党可以做到让大家都选 $\beta$ ，因为能够带有强制性，否则小命不保。

结论三：汝欲得之，必先知之。

说白了就是在选择策略的时候，一定要想清楚你的收益，是只考虑成绩，还是同时要考虑同桌关系，社会地位等等。只有明确了收益，才能方便做策略选择。

对于上述的博弈，我们稍微修改一下收益矩阵，如果我得了A，我同桌得了C，我可能因为背叛他而产生负罪感，导致我的收益-4，从而收益变为了 $3-4=-1$ 。如果我得了C，我同桌得了A，我可能无法和家人交代，导致我的收益-2，从而收益变成了 $-1-2=-3$ 。

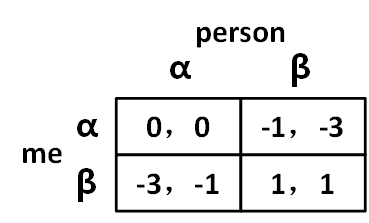
现在我们再重新进行分析。

第一种情况，我的同桌选择了策略 $\alpha$ ，那么我选择策略 $\alpha$ 的时候，我的收益是0，我选择策略 $\beta$ 时，我的收益是-3。 $0 > -3$ ，即我应该选择策略 $\alpha$ 。

第二种情况，我的同桌选择了策略 $\beta$ ，那么我选择策略 $\alpha$ 的时候，我的收益是-1，我选择策略 $\beta$ 时，我的成绩是1。 $-1 < 1$ ，即我应该选择策略 $\beta$ 。

此时，不存在严格优势策略。也就印证了结论三。在进行决策之前，一定想清楚你的收益是什么？

我们将博弈再进行一次变形。针对第一个博弈的收益，我们称作参与者为恶鬼(Evil Gits，EG)，针对第二个博弈的收益(即有负罪感的那种)，我们称作参与者为天使(Indignant Angel，IA)。那种第一种博弈是EG vs EG，第二种博弈是IA vs IA。那么如果是EG vs IA呢？博弈矩阵可以写作如下（假设我是IA）：

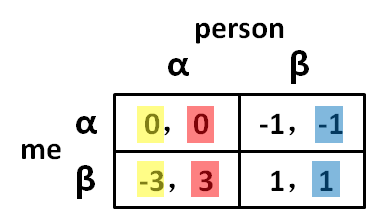
如果我同桌选择 $\alpha$ ，我选择 $\alpha$ 收益是0， $\beta$ 是-3，所以 $\alpha$ 优于 $\beta$ 。

如果我同桌选择 $\beta$ ，我选择 $\alpha$ 收益是-1， $\beta$ 是1，所以 $\beta$ 优于 $\alpha$ 。

那么站在我的角度似乎没有严格优势策略。

但是如果换位思考：

我选 $\alpha$ 时，对方选 $\alpha$ 收益是0， $\beta$ 是-1。所以 $\alpha$ 优于 $\beta$ 。

我选 $\beta$ 时，对方选 $\alpha$ 收益3， $\beta$ 是1。所以 $\alpha$ 优于 $\beta$ 。

那么我们可以发现，对方是存在严格优势策略 $\alpha$ 的，所以我的策略应该选择 $\alpha$ 。

结论四：站在别人的立场去分析他们会怎么做。

结论五：耶鲁的学生很自私。

结论五有种开玩笑的意思，但其实也是想表达：在分析博弈时，大前提就是所有参与者都会最大化自己的收益。

下课前布置的一个博弈：选数游戏:从 $1$ 到 $100$ 之间选择一个号码填到下面的方框内，不要让你的同桌看到，我们会计算全班的平均数，谁选的数字最接近平均数的 $\frac{2}{3}$ ，谁就是赢家。