网络算法系列之图嵌入（一）：离线采样方法 Alias MethodAlias Method是一个采样方法，针对带权重的随

Alias Method是一个采样方法，针对带权重的随机采样问题。它的空间复杂度是 $O(n)$ ，时间复杂度为 $O(1)$ 。外站有一个博客写的非常好：Darts, Dice, and Coins: Sampling from a Discrete Distribution

举个例子

在游戏中，当我们打败一个boss后，会有一些不同稀有度物品的掉落判定，假定掉落白色物品的概率是 $\frac{1}{2}$ ，蓝色物品的概率是 $\frac{1}{3}$ ，紫色和橙色物品的概率均是 $\frac{1}{12}$ 。如何能够生成一个物品掉落的序列，使它满足这个概率分布？

通常能想到的有两种解决办法：

第一种：构造一个长度为12的数组 $\alpha$ ，其中6个标记为白色，4个标记为蓝色，1个标记为紫色，1个标记为橙色。而后取一个12以内的随机数 $m=randint()\%12$ 作为数组的下标，那么 $\alpha(m)$ 即为掉落的物品。此方法时间复杂度为 $O(1)$ ，但是空间复杂度不理想，虽然看起来我们申请的长度只有12，但是如果我们将橙色掉落概率为 $0.01\%$ ，那么就需要申请一个长度为 $10000$ 的数组。

第二种：直接构造一个累积概率序列 $\{\frac{6}{12},\frac{10}{12},\frac{11}{12},\frac{12}{12}\}$ ，随机生成一个0-1的随机数 $m=rand()$ ，譬如 $m=0.9$ ，然后查找 $m$ 落在那个区间 $(\frac{10}{12},\frac{11}{12})$ 中，故判定为紫色物品。此种方法空间复杂度是 $O(n)$ ，如果是线性查找，时间复杂度是 $O(n)$ ，如果是二分查找，时间复杂度是 $O(\log n)$ 。

那么是否有时间复杂度更低的方法呢？

一个想法

我们不妨将分步考虑：

第一步，我们产生一个 $1$ ~ $4$ 的随机数 $m$ ，譬如 $m=2$ ，就表示要掉落蓝色物品。

第二步，我们再产生一个0-1的掉落概率 $n$ ，譬如 $n=0.2<\frac{1}{3}$ ，故掉落成功。如果 $n=0.9>\frac{1}{3}$ ，则掉落失败，同时重新进行第一步循环，直至掉落物品。此种方法，最好的情况，时间复杂度为 $O(1)$ ，最差则为无穷次。故平均复杂度仍为 $O(n)$ 。

那么是否有改进的办法呢？

Alias Method

我们先得到初始的概率分布：

因为初始类别 $K=4$ ，所以我们将所有的概率乘上 $4$ ，来保证最后的高度都是 $1$ 。

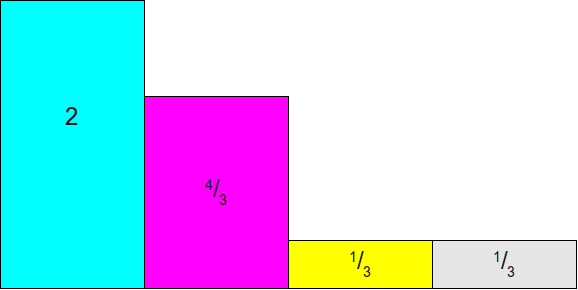
之后，我们需要通过拼凑的方法，将每个列的高度都拼凑为1，同时保证每个列至多只有两种类别。这种做的好处就是避免抽样失败的情况出现，相当于用其他的类别(蓝色or紫色)来替代抽样失败(棕色)的情况。alias就是用来填充失败的类别。

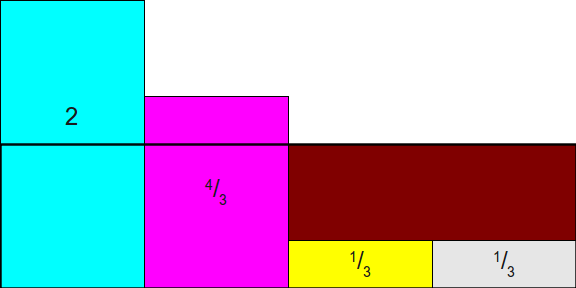经过替换后，我们可以得到下图：

至此，我们就将概率都拉平为1，得到了上图结果，从而可以得到下述两个table：

第一个是Probability table，即能够得到原本类别的概率数组 $Prob$ ： $[\frac{2}{3},1,\frac{1}{3},\frac{1}{3}]$ 。

第二个是Alias table，即当不属于本类别后，具体将归属于其他的哪个类别（即用来填充失败概率的类别）的数组 $Alias$ ： $[2,Null,1,1]$ 。

至此，我们就完成了上述的Alias Method的初始化。采样过程如下：

1、根据类别数K，随机生成一个K以内的随机数 $m=randint()\%K$ 。

2、在生成一个0-1的随机数 $n=rand()$ 。

3、如果 $n < Prob[m]$ ，则类别为 $m$ ，否则为 $Alias[m]$ 。

我们可以验证一下，掉落白色物品的概率为： $\frac{2}{3} * \frac{1}{4}+(1-\frac{1}{3}) * \frac{1}{4}+(1-\frac{1}{3}) * \frac{1}{4} = \frac{1}{2}$ 。完全符合！

Alias Table的构建

现在的问题转换为了如何根据概率分布序列构建这样一个Alias Table，并且是否任意的概率序列都能构建出的Alias Table呢？

存在性证明

任意的概率序列都能构建出Alias Table，具体证明可以参考文章开头提到的博客。

构建的实现

可以采用两个队列去分别存储小于1和大于1的类别，假设记为smaller和larger。每次从smaller和larger中各取一个类别，记为small和large。将large去填充small（由于large>1，故一定能填充满small，且small一定满足只有两种类别构成，即small和large）。此时small一定为1，即可退出队列。再根据剩下的large是否大于1，将它放入smaller或者larger的队列中。直至所有的类别都满足为1。

代码如下（参考Alias Method 代码）：

# !/usr/bin/env python
# encoding: utf-8

import time
import numpy as np
import pandas as pd
import numpy.random as npr

def alias_setup(probs):
    
    :param probs: 某个概率分布
    :return: Alias数组与Prob数组
    
    K =len(probs) # K为类别数目
    Prob =np.zeros(K) # 对应Prob数组：落在原类型的概率
    Alias =np.zeros(K,dtype=np.int) # 对应Alias数组：每一列第二层的类型

    #Sort the data into the outcomes with probabilities
    #that are larger and smaller than 1/K
    smaller =[] # 存储比1小的列
    larger =[] # 存储比1大的列

    for kk,prob in enumerate(probs):
        Prob[kk] =K*prob # 概率（每个类别概率乘以K，使得总和为K）
        if Prob[kk] <1.0: # 然后分为两类：大于1的和小于1的
            smaller.append(kk)
        else:
            larger.append(kk)

    # Loop though and create little binary mixtures that appropriately allocate
    # the larger outcomes over the overall uniform mixture.

    #通过拼凑，将各个类别都凑为1
    while len(smaller) > 0 and len(larger) > 0:
        small = smaller.pop()
        large = larger.pop()

        Alias[small] = large #填充Alias数组
        Prob[large] = Prob[large]-(1.0 - Prob[small]) #将大的分到小的上

        if Prob[large] <1.0:
            smaller.append(large)
        else:
            larger.append(large)
    print("Prob is :", Prob)
    print("Alias is :", Alias)
    return Alias,Prob

def alias_draw(Alias,Prob):
    '''
    :param J: Alias数组
    :param q: Prob数组
    :return:一次采样结果
    '''
    K=len(Alias)

    # Draw from the overall uniform mixture.
    kk = int(np.floor(npr.rand()*K)) #随机取一列

    # Draw from the binary mixture, either keeping the small one, or choosing the associated larger one.
    # 采样过程：随机取某一列k（即[1,4]的随机整数，再随机产生一个[0-1]的小数c，）
    # 如果Prob[kk]大于c，
    if npr.rand() <Prob[kk]: #比较
        return kk
    else:
        return Alias[kk]

if __name__ == '__main__':
    start=time.time()

    K = 5  # K初始化为5类
    N = 5

    # Get a random probability vector.
    # probs = npr.dirichlet(np.ones(K), 1).ravel()  # .ravel(): 将多维数组降为一维
    probs =[0.2,0.3,0.1,0.2,0.2]
    # Construct the table
    Alias, Prob = alias_setup(probs)

    # Prob is : [ 0.25058826  0.69258202  0.83010441  0.87901003  1.        ]
    # Alias is : [4 4 4 4 0]
    ######

    # Generate variates.
    # X 为有多少样本需要采样
    X = np.zeros(N)
    for nn in range(N):
        X[nn] = alias_draw(Alias, Prob)
    print("最终的采样结果X为：",X)

    end=time.time()
    spend=end-start
    print("耗时为：%0.4f s"%spend)

    sure_k = np.random.choice(5, 1, p=probs)
    print("surek为：",sure_k)
    # 关于SEM的并行，我先尝试了在 sample k 的时候使用Alias Method，但是和之前比效率方面没见得有提升（之前SEM是利用  sure_k = np.random.choice(aspects_num, 1, p=p) 进行sample k的）
    # Alias必须是多次采样才有效率上的提升的。如果每一次sample都新来一次alias那是没有用的