LeetCode Container With Most Water（011）解法总结Given n non-negat

描述

Given n non-negative integers a₁, a₂, ..., a_n, where each represents a point at coordinate (i, a_i). n vertical lines are drawn such that the two endpoints of line i is at (i, a_i) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

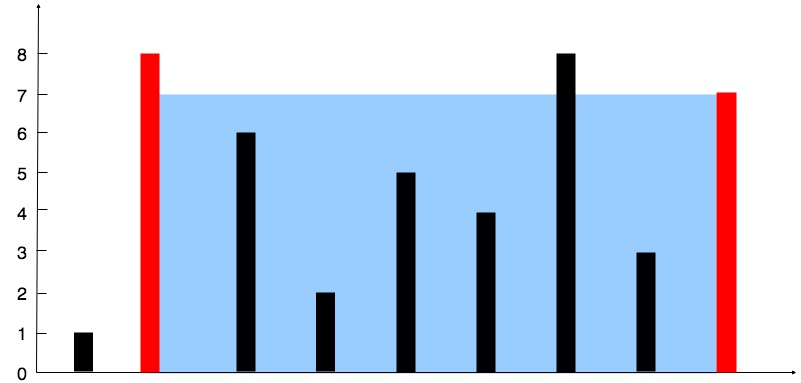
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example:

Input: [1,8,6,2,5,4,8,3,7]
Output: 49

思路

生成一个二维数组，计算每两个挡板之间的存水量，时间复杂度均为O(n^2)。

class Solution {
    public int maxArea(int[] height) {
        int out = 0;
        for(int i = 0; i<height.length; i++){
            for(int j = 0; j<=i; j++){
                out = Math.max(out,((i - j) * Math.min(height[i], height[j])));
            }
        }
        return out;
    }
}

Runtime: 370 ms, faster than 9.73% of Java online submissions for Container With Most Water.

Memory Usage: 41.3 MB, less than 5.77% of Java online submissions for Container With Most Water.

可以看出时间消耗确实很高。

优化

评论区发现一种思路，当有一边的挡板高度大于另一边时，将高的那边的index向中间收缩不会得到更大的值，因为宽和高一定都会缩短。

The max area is calculated by the following formula:

S = (j - i) * min(ai, aj)

We should choose (i, j) so that S is max. Note that i, j go through the range (1, n) and j > i. That's it.

The simple way is to take all possibilities of (i, j) and compare all obtained S. The time complexity is n * (n-1) / 2

What we gonna do is to choose all possibilities of (i, j) in a wise way. I noticed that many submitted solutions here can't explain why when :

ai < aj we will check the next (i+1, j) (or move i to the right)
ai >= aj we will check the next (i, j-1) (or move j to the left)

Here is the explaination for that:

When ai < aj , we don't need to calculate all (i, j-1), (i, j-2), .... Why? because these max areas are smaller than our S at (i, j)

Proof: Assume at (i, j-1) we have S'= (j-1-i) * min(ai, aj-1)
S'< (j-1-i) * ai < (j-i) * ai = S, and when S'<S, we don't need to calculate
Similar at (i, j-2), (i, j-3), etc.

So, that's why when ai < aj, we should check the next at (i+1, j) (or move i to the right)

When ai >= aj, the same thing, all (i+1, j), (i+2, j), .... are not needed to calculate.

We should check the next at (i, j-1) (or move j to the left)

下面是实现：

class Solution {
    public int maxArea(int[] height) {
        int i = 0, j = height.length -1, s = 0;
        while(i != j){
            s = Math.max(s, ((j - i) * Math.min(height[i], height[j])));
            if(height[i] < height[j]){
                i++;
            }else{
                j--;
            }
        }
        return s;
    }
}

Runtime: 2 ms, faster than 95.46% of Java online submissions for Container With Most Water.

Memory Usage: 41.4 MB, less than 5.77% of Java online submissions for Container With Most Water.

避免循环还是能够节约很多时间的。