小码哥《恋上数据结构与算法第二季》笔记（四）：快速排序（Quick Sort）从序列中选择一个轴点元素（pivot）,假

我的Github地址

小码哥《恋上数据结构与算法》笔记

极客时间《iOS开发高手课》笔记

iOS大厂面试高频算法题总结

iOS面试资料汇总

快速排序（Quick Sort）

一、概念

从序列中选择一个轴点元素（pivot）,假设每次选择0位置的元素为轴点元素。
利用pivot将序列分割成2个子序列，将小于pivot的元素放在pivote前面（左侧），将大于pivot的元素放在pivot后面（右侧），等于pivot的元素放在哪边都可以。
对子序列进行上一步操作，直到不能再分割（子序列中只剩下1个元素）。
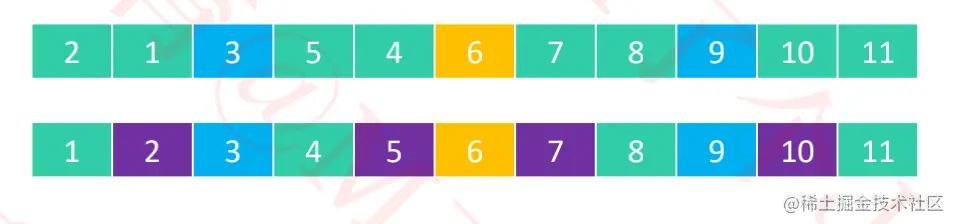
快速排序的本质：逐渐将每个元素都转换成轴点元素。

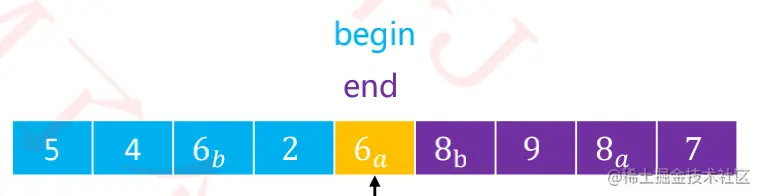
二、轴点构造

将6作为轴点，备份一份。
从右边（end）开始扫描数组。
扫描7，大于6a，执行end--即可。
扫描5，小于6a，用5覆盖6a的位置，begin++。
下一步，从左边（begin）继续扫描。
扫描8a，大于6a，用8a覆盖5的位置，end--。
下一步，从右边（end）继续扫描
扫描9，大于6a，执行end--，不做其他操作。
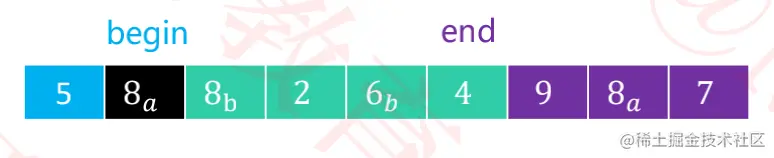
扫描4，小于6a，用4覆盖8a的位置，begin++。
扫描8b，大于6a，用8b覆盖4的位置，end--。
扫描6b，等于6a，用6b覆盖8b的位置，begin++。
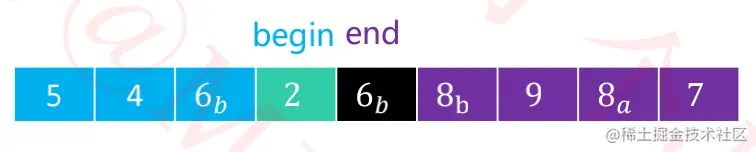
扫描2，小于6a，begin++。
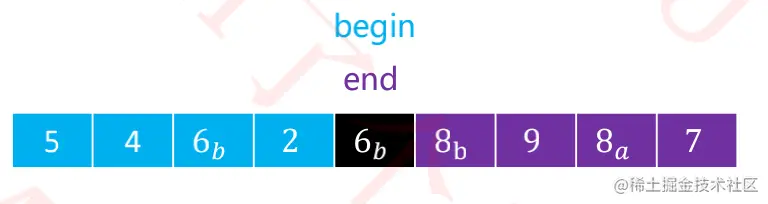
当发现begin和end重叠，则轴点构造完成。将备份的6a，覆盖6b的位置。

三、代码实现

public class QuickSort<T extends Comparable<T>> extends Sort<T> {

	@Override
	protected void sort() {
		sort(0, array.length);
	}

	/**
	 * 对 [begin, end) 范围的元素进行快速排序
	 * @param begin
	 * @param end
	 */
	private void sort(int begin, int end) { 
		if (end - begin < 2) return; //至少有两个元素才执行快速排序
		
		// 确定轴点位置 O(n)，并进行一次快速排序
		int mid = pivotIndex(begin, end);
		// 对子序列进行快速排序
		sort(begin, mid); 
		sort(mid + 1, end); 
	} 
	
	/**
	 * 构造出 [begin, end) 范围的轴点元素，并进行一次快速排序
	 * @return 轴点元素的最终位置
	 */
	private int pivotIndex(int begin, int end) {
		// 为了降低最坏情况(O(n^2)的时间复杂度)的出现概率，随机选择一个元素跟begin位置进行交换
		swap(begin, begin + (int)(Math.random() * (end - begin)));
		
		// 备份begin位置的元素
		T pivot = array[begin];
		// end指向最后一个元素
		end--;
		
		// 如果begin == end 则退出排序
		while (begin < end) {
			while (begin < end) {
				if (cmp(pivot, array[end]) < 0) { // 右边元素 > 轴点元素
					end--; // 只位移，不进行元素交换
				} else { // 右边元素 <= 轴点元素
					array[begin++] = array[end];
					break; //执行完一次操作后，需要掉头，所以执行一个break
				}
			}
			while (begin < end) {
				if (cmp(pivot, array[begin]) > 0) { // 左边元素 < 轴点元素
					begin++;
				} else { // 左边元素 >= 轴点元素
					array[end--] = array[begin];
					break; // 通过两个break，能实现两个while交替执行。
				}
			}
		}
		
		// 将轴点元素放入最终的位置
		array[begin] = pivot;
		// 返回轴点元素的位置
		return begin;
	}
}

在当前算法，如果序列中的元素a与轴点元素相等，则会将轴点元素与元素a替换位置。
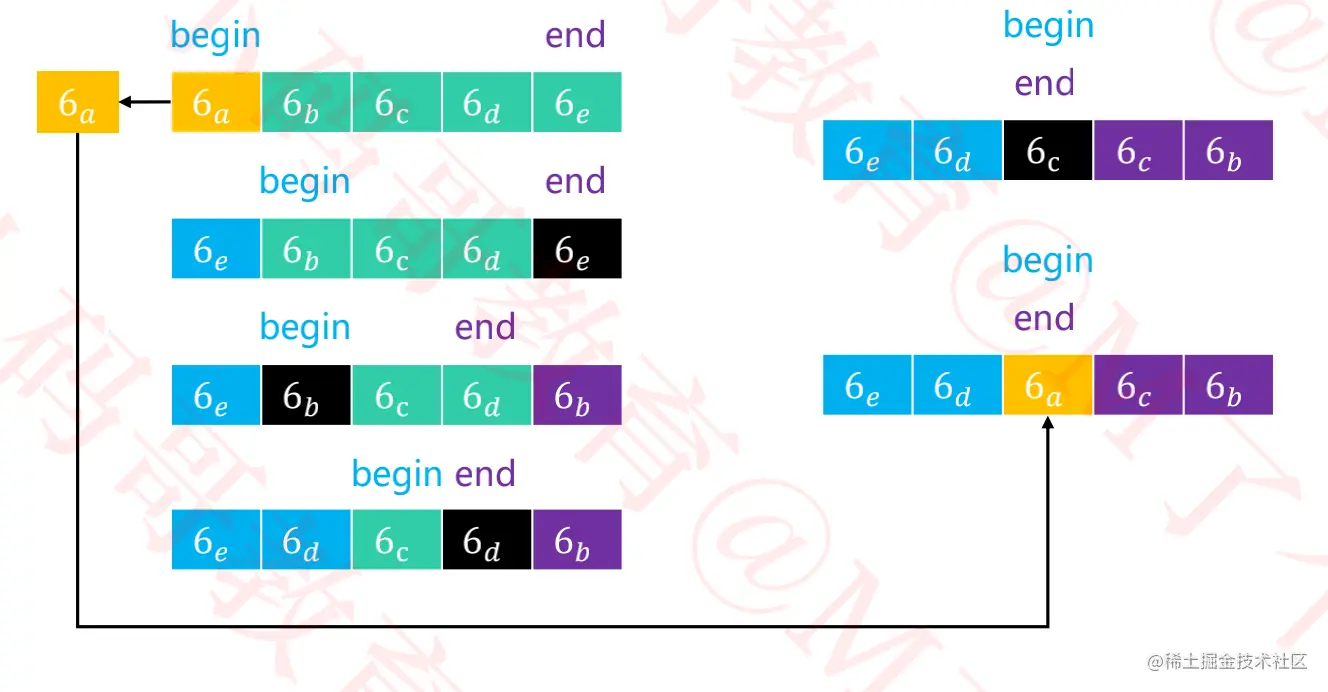
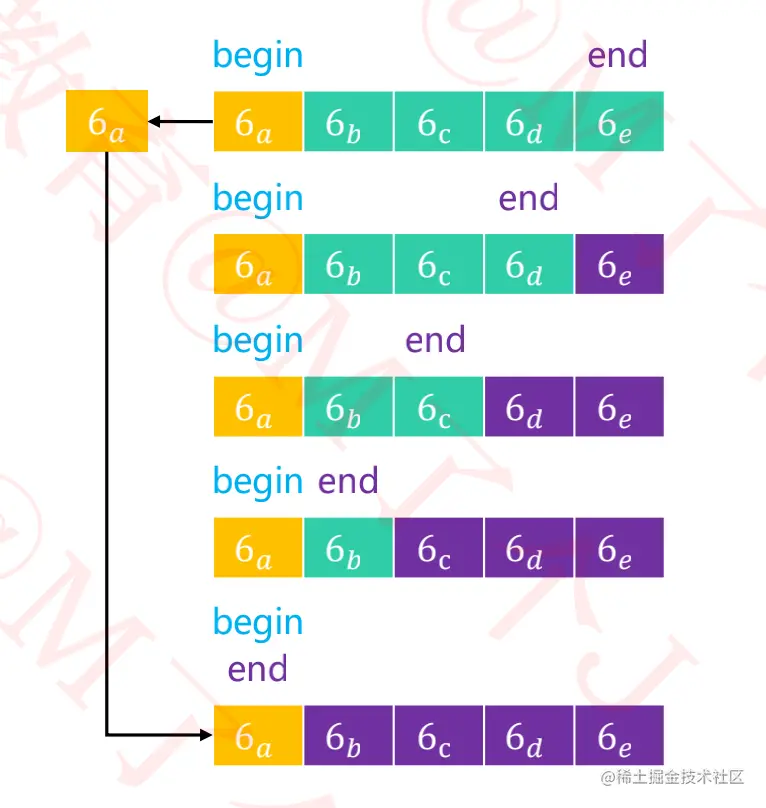
如果元素a与轴点元素相等时，不进行替换，那么最终得到的数组会非常不平衡（黄色轴点在数组中的位置），导致出现最坏时间复杂度O(n^2)。

四、时间复杂度

在轴点左右元素数量比较均匀的情况下，同时也是最好的情况，时间复杂度是O(nlogn)。
如果轴点左右元素数量极度不均匀，最坏情况是O(n^2)。
为了降低最坏情况的出现概率，一般采取的做法是随机选择轴点元素。
由于递归调用的缘故，空间复杂度是：O(logn)。
快速排序属于不稳定排序。