深度学习中指数加权移动平均（EWMA）优化方法及其发展本文将要介绍神经网络优化算法中的Momentum算法，RMSPro

本文将要介绍神经网络优化算法中的Momentum算法，RMSProp算法和Adam算法。资料来自于fastai课程和Ng的深度学习课程。

1.Momentum算法

Momentum算法，又称动量法，直接使用了EWMA的思想，即指数加权移动平均法。在进行本次优化时，令之前几次优化的梯度大小和方向对本次优化的向量大小和方向产生较大影响，因为前面的优化大小和方向能很好的反映近期变化的趋势，从而达到了加速模型拟合的效果，优化了拟合路线。

用公式表达为：

$v_t=βv_{t−1}+(1−β)θ_t$

$\omega = \omega - v_t$

如图所示，如果把蓝色箭头看作 $v_t$ ，则绿色箭头为 $v_{t-1}$ ，而 $\theta_t$ 为本次优化(即蓝色箭头)的梯度值，通常我们令β=0.9，则 $v_{blue}=0.9v_{green}+0.1θ_{blue}$ 。

如果把优化向量称作“步数”，则本次优化的步数=上次优化的步数*β+本次优化的梯度*(1-β)。需要优化的权重

但是，这里存在两个问题：

问题一：

由上面的公式可以得出，第一次进行优化时 $v_1=βv_0+(1-β)θ_1$ ，而 $v_0=0$ ，这样就导致前期的迭代过程中优化的步数很小，拟合速度很慢。

如图，理想效果为绿色曲线，而实际为紫色曲线。当迭代次数不断增大时，两曲线才慢慢的重合在一起，这是因为当迭代次数变大时当前步数受前几次优化的步数影响就很小了。

所以，可以将公式改写为： $v_t=\frac{βv_{t−1}+(1−β)θ_t}{1-β^t}$

这样的话，当迭代次数t较小时，可以将原本的迭代步数放大；而当迭代次数较大时，分母趋近于1，对原本的迭代步数没有影响。

问题二：

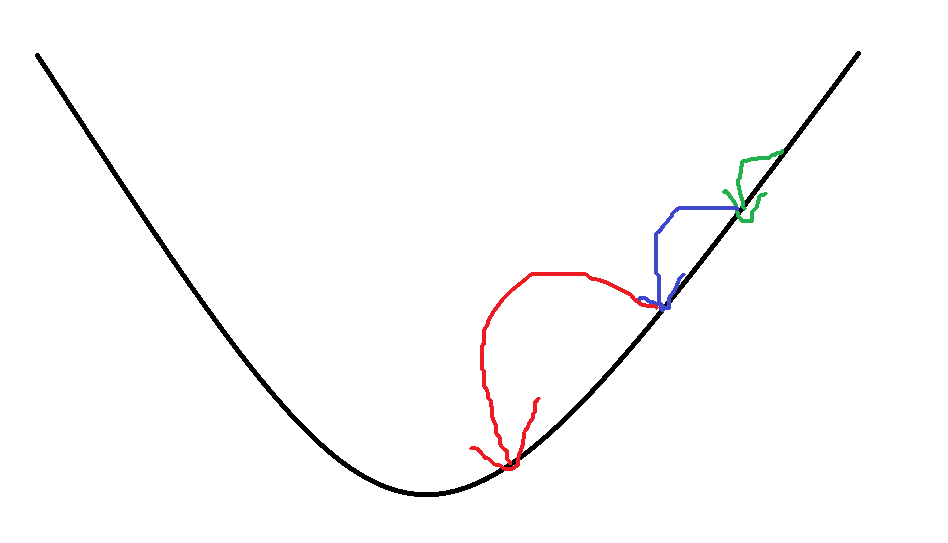
如果移动平均数不断增大，会导致梯度爆炸的问题，如下图。且拟合路线波动的问题并没有解决。

为了解决这个问题，RMSProp算法诞生了。

自适应学习率调整。 RMSProp算法在momentum算法的基础上做了改进，用mom算法的超参数β和学习率α同时制约本次移动的步数。

公式为：

$s_t=βs_{t−1}+(1−β)θ_t^2$

$\omega = \omega - \frac{αθ_t}{\sqrt{s_t}}$

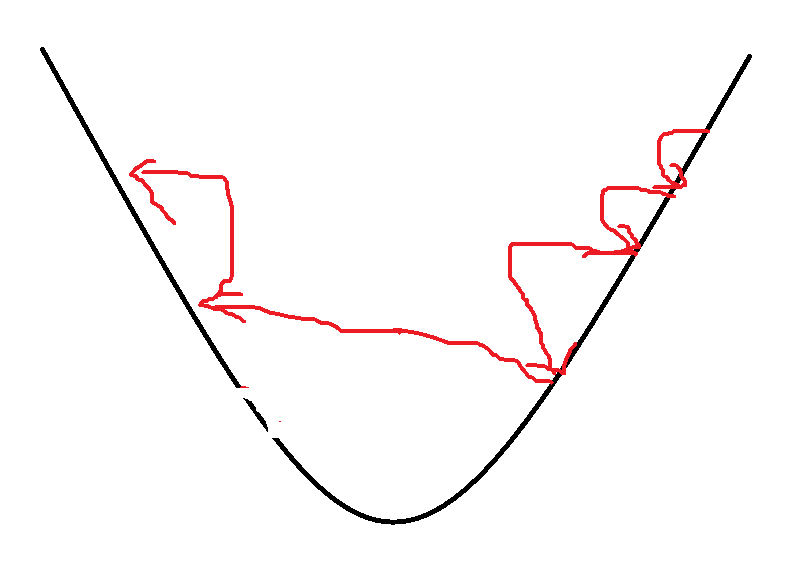
这样，本次优化的步数在本次梯度和学习率的影响的基础上，受到了前面累积的移动平均数的制约，相当于将梯度下降法与动量法相结合，使得优化路线波动更小，收敛速度更快。

如图，蓝色为mom算法优化路线，绿色为RMSProp算法优化路线。

Adam算法实质上就是把mom法和RMS法又进行了一次叠加，以期得到更好的效果。进一步放大了RMS法中，之前优化的步数对本次优化步数的影响。

公式：

$v_t=βv_{t−1}+(1−β)θ_t$

$s_t=βs_{t−1}+(1−β)θ_t^2$

$\omega = \omega - \frac{αv_t}{\sqrt{s_t}}$

对于Adam算法来说，其实是将动量法和梯度下降法做了较好的融合，但是在动量法的问题一中所提到的问题依然存在，因此可以用同样的方法优化公式。