一文扫清【冒泡排序、插入排序、快速排序】的盲点
原文就是笔者写的,只不过首发在了 CSDN 上,原文链接 : 一文扫清【冒泡排序、插入排序、快速排序】的盲点 - CSDN【萍果吮雨】
前言 :
说到底笔者还是对算法不感冒的,本文论述也只是建立在目前自己的水平和理解上,如有错处或争议之处还请各路大神斧正。本文涉及到公共领域的人物或事件均无炒作和扩大矛盾的意思,只想着为本文稍加润色,本文会尽量揭示核心原理,时间复杂度和空间复杂度暂不作探讨。本文全局使用的测试数组为 : [2, 1, 5, 0, 6, 3]
冒泡排序
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。--- 百度百科
冒泡排序 - 经典版
经典版是对冒泡排序最直观和通俗易懂的实现。
冒泡排序 - 经典版(图解原理)
以数组 [2, 1, 5, 0, 6, 3] 为例
第一轮循环 i = 0 j=[0 ~ 4]
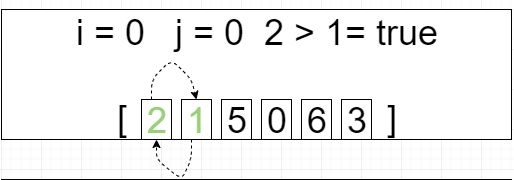
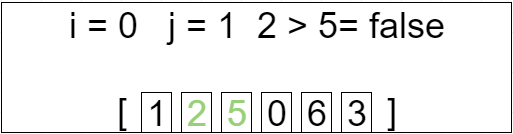
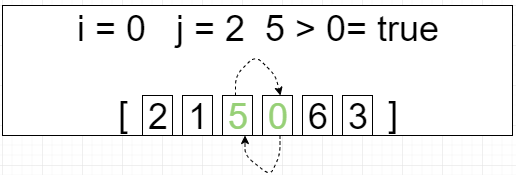
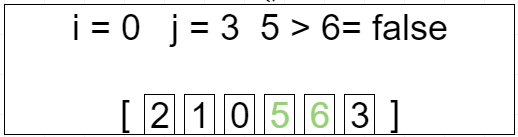
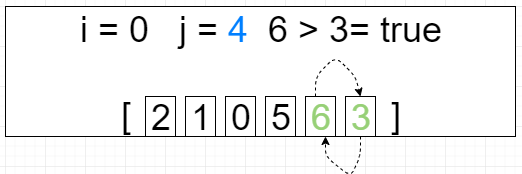
[2, 1, 0, 5, 3, 6]
第二轮循环 i = 1 j=[0 ~ 3]
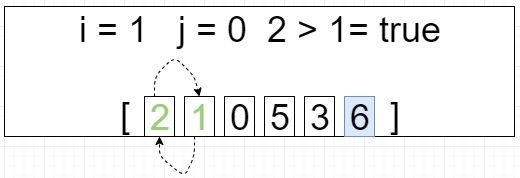
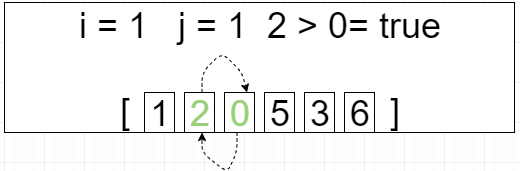
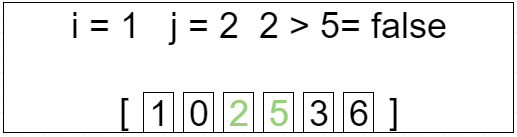
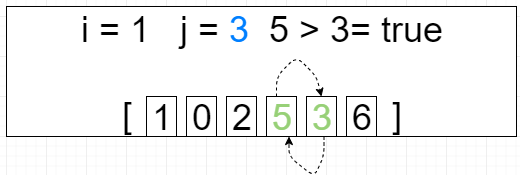
[2, 1, 0, 3, 5, 6]
第三轮循环 i = 2 j=[0 ~ 2]
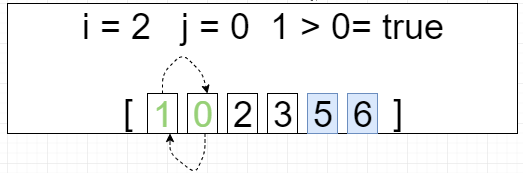
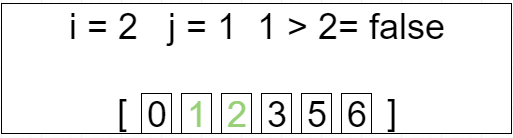
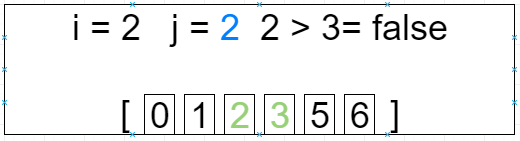
[0, 1, 2, 3, 5, 6]
第四轮循环 i = 3 j=[0 ~ 1]
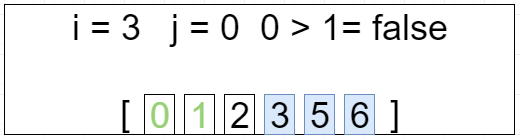
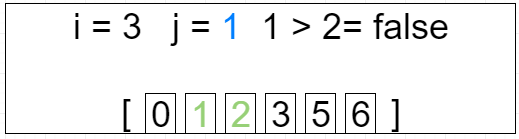
[0, 1, 2, 3, 5, 6]
第五轮循环 i = 4 j=[0 ~ 0]
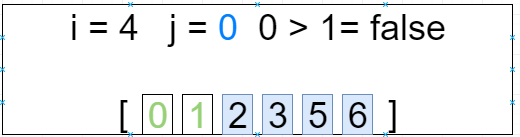
[0, 1, 2, 3, 5, 6]
最终数组为 : [0, 1, 2, 3, 5, 6]
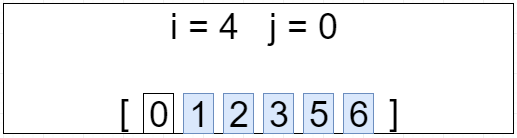
冒泡排序 - 经典版(代码实现)
let arr = [2, 1, 5, 0, 6, 3];
// 定义排序数组
let sortedArr = arr.slice();
// 定义临时存储待交换元素的临时容器变量
let temp = 0;
for(let i = 0; i < sortedArr.length - 1; i++) {
for(let j = 0; j < sortedArr.length - i - 1; j++) {
if(sortedArr[j] > sortedArr[j + 1]) {
temp = sortedArr[j];
sortedArr[j] = sortedArr[j + 1];
sortedArr[j + 1] = temp;
}
}
}
console.log("排序前的数组 :");
console.log(arr);
console.log("排序后的数组 :");
console.log(sortedArr);
冒泡排序 - 经典版(需要明确的点)
冒泡排序 - 经典版的这个代码比较好理解,需要注意的地方就是 :
- 外层 for 循环控制的是参与排序的元素个数, 例如上述排序的数组, 共有 6 个元素如果 5 个都已经确定位置了那剩下那一个就也没必要去和其它元素比对了,因为剩下的那个元素也一定是已经被排好序的,所以外层 for 循环要循环 arr.length - 1 次 也就是 5 次。
- 内层 for 循环控制的是元素比对的次数, 上述数组在比对的时候每轮都会确定一个较大的数放在数组尾部,这样一来下一次循环的时候就没有必要和已经确定在数组尾部的诸多较大的元素去比对了,只要和其前面的元素比对即可,如此循环往复,最后排到数组最开头的两个元素 .... 排序结束,又因为内部 for 循环的比对条件是
arr[j] > arr[j + 1]且 i 又是递增的所以光 arr.length - i肯定不行,因为假设当前是第一轮循环 i = 0, j < arr.length - i => j < 6 .... 比对到内部 for 循环的最后发现 arr[5] > arr[6],数组一共 6 个元素哪来的索引 6 ? 所以这样执行会导致结果不准确(如果是强类型语言直接报错"数组下标越界"), 故内层 for 循环的迭代条件要为 arr.length - 1。
冒泡排序 - 升级版
所谓升级版就是在相邻元素交换的过程做了优化,采用位运算符的方式操纵底层二进制码来实现快速交换元素。
冒泡排序 - 升级版(图解原理)
- 整体的排序逻辑与
经典版一致,不同的只是相邻元素交换的方式。 - 下面图解主要解释使用位运算符怎么实现两数交换。
- 先运行如下代码 :
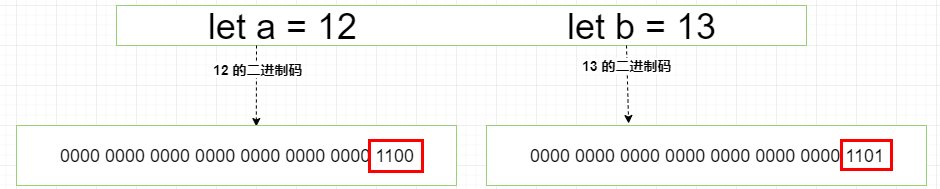
let a = 12;
let b = 13;
console.log(a, b); // 12, 13
a = a ^ b;
b = a ^ b;
a = a ^ b;
consle.log(a, b); // 13, 12
图解交换过程 :
- 初始时候 a = 12 且 12 的 二进制码、b = 13 且 13 的二进制码
- 执行
a = a ^ b
- 执行
b = a ^ b;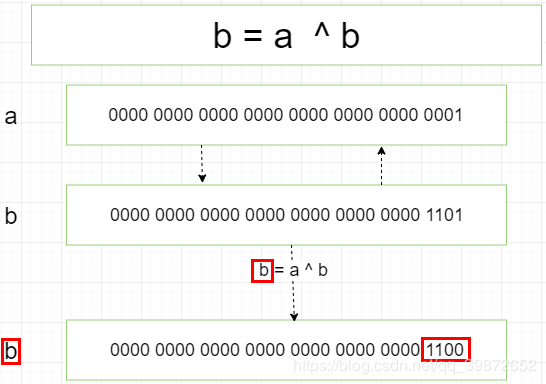
- 执行
a = a ^ b

冒泡排序 - 升级版(代码实现)
let arr = [2, 1, 5, 0, 6, 3];
// 定义排序数组
let sortedArr = arr.slice();
// 定义临时存储待交换元素的临时容器变量
for(let i = 0; i < sortedArr.length - 1; i++) {
for(let j = 0; j < sortedArr.length - i - 1; j++) {
if(sortedArr[j] > sortedArr[j + 1]) {
sortedArr[j] = sortedArr[j] ^ sortedArr[j + 1];
sortedArr[j + 1] = sortedArr[j] ^ sortedArr[j + 1];
sortedArr[j] = sortedArr[j] ^ sortedArr[j + 1];
}
}
}
console.log("排序前的数组 :"); // 排序前的数组 :
console.log(arr); // [2, 1, 5, 0, 6, 3]
console.log("排序后的数组 :"); // 排序后的数组 :
console.log(sortedArr); // [0, 1, 2, 3, 5, 6]
冒泡排序 - 升级版(需要明确的点)
^【异或】位操作符的运算规则是两个操作数码的码值对比不同才为 1 , 相同都为 0 。- 使用位运算符会加快交换相邻元素的速度,因为直接操作的是底层的二进制码。
- 如果对位运算符不了解的朋友, 请移步至 JavaScript 中的运算符。 最后借助动图来理解一下整体交换过程
由于种种原因 : [2, 1, 5, 0, 6, 3] 数组被换成了 [2, 1, 5, 1, 6, 3]。不过不耽误演示
1与0差不太多。
插入排序
插入排序的基本思想是:每步将一个待排序的记录,按其关键码值的大小插入前面已经排序的文件中适当位置上,直到全部插入完为止。--- 百度百科
所以本案例就假定第一个元素是确定排好序的, 在本案例数组中也就是 2 这个元素是默认排好序的, 这就将整个集合分成两部分, 一部分是已排好序的, 另一部分是未排好序的,然后迭代未排好序的部分向已排好序的部分中的指定位置插入元素,直到未排好序的部分的元素全部插入完毕则整个集合排序完毕。
图解原理
-1). 整体流程图解 :
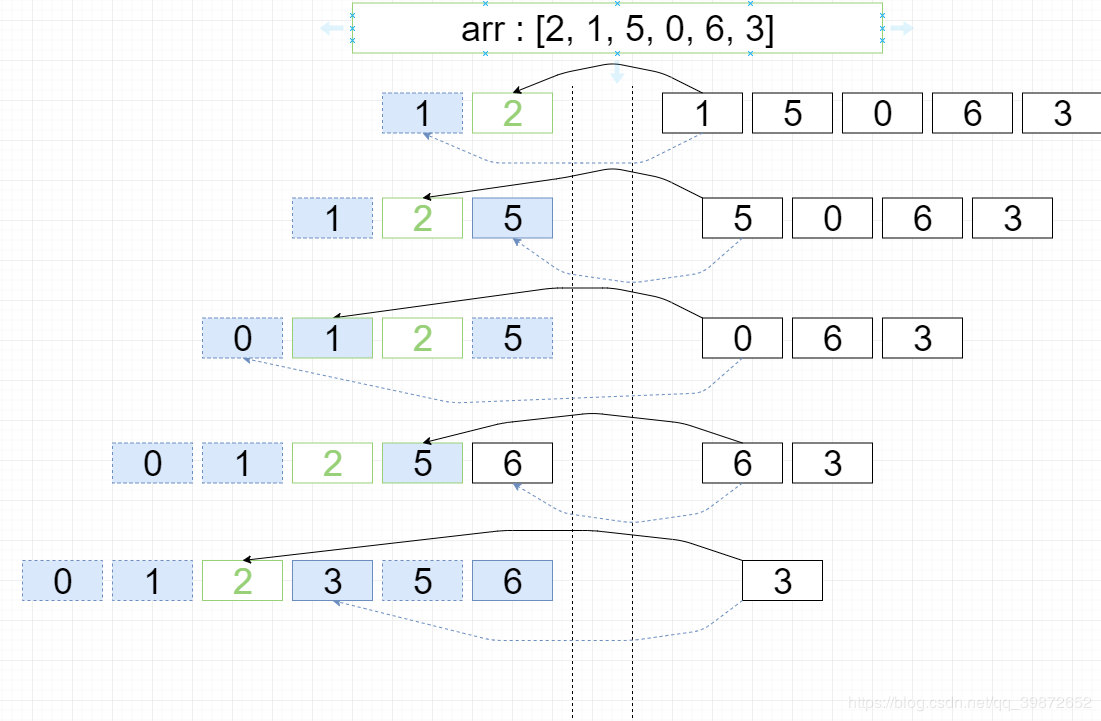

[1, 2, 0, 5, 6, 3]
第一轮循环 i = 2 j=[0 ~ 1]


[0, 1, 2, 5, 6, 3]
第三轮循环 i = 3 j=[0 ~ 2]



[0, 1, 2, 5, 6, 3]
第四轮循环 i = 4 j=[0 ~ 3]

[0, 1, 2, 5, 6, 3]
第五轮循环 i = 5 j=[0 ~ 4]
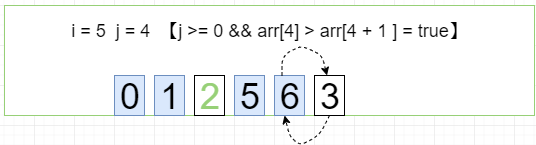
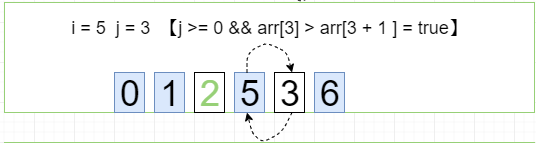

[0, 1, 2, 3, 5, 6]
故数组最终为 : [0, 1, 2, 3, 5, 6]
代码实现
// 克隆数组防止影响原数组
let sortedArr = arr.slice();
// 定义临时存储待交换元素的临时容器变量
for(let i = 1; i < sortedArr.length; i++) {
for(let j = i - 1; j >= 0 && sortedArr[j] > sortedArr[j + 1]; j--) {
sortedArr[j] = sortedArr[j] ^ sortedArr[j + 1];
sortedArr[j + 1] = sortedArr[j] ^ sortedArr[j + 1];
sortedArr[j] = sortedArr[j] ^ sortedArr[j + 1];
}
}
需要明白的点 :
- 外层 for 循环 i 的索引要从 1 开始,因为我们是假定第一个元素已经排好序了。
- 内层 for 循环每轮 j 的索引的初始值是 i - 1,是因为在比对的时候要从第一个元素开始比,j-- 是控制待比较元素不断的与前一个元素进行比较的,因为只有 j-- 才能通过
arr[j] > arr[j+1]不断的向前比较。所以就确定了 j 必须是个变量,在外层只有 i 是递增的变量所以 i 与 j要产生关系,但 j 不能直接等于 i。因为如果是这样当 i = 5 ,的时候 arr[j + 1] => arr[5 + 1] => arr[6] ,数组里只有 6 个元素哪来的索引 6 ?,所以这样去比较,会产生误差,故 j 要等于 i - 1 来确定每次 j 的初始值, - 内存层循环中 j >= 0,是因为每个待排序元素都是从当前的位置要一直比到数组开头的,所以 j 的所以可以是 0 但不能是 -1,故 j >= 0。
- 外层 for 循环控制的是有多少个
最后借助动图来理解一下整体交换过程
由于种种原因 : [2, 1, 5, 0, 6, 3] 数组被换成了 [2, 1, 5, 1, 6, 3]。不过不耽误演示
1与0差不太多。
快速排序
快速排序之争
"之争" 有些过了,不过上网查资料的时候发现,阮神被喷了! 贴图 :
阮氏快排
个人感觉阮老师的实现如果放在教科书上讲解快排思想是非常不错的,通俗易懂! 原文链接 : 网络同行纷纷吐槽说每次递归都创建新数组增加了空间复杂度云云,具体细节不便评说 :
阮氏快排(代码实现)
var quickSort = function(arr) {
if (arr.length <= 1) {return arr; }//判断数组,一个长度直接返回
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];//找出基准元素
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
//循环把元素分别放入左边和右边数组
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};
console.log(quickSort([2, 1, 5, 0, 6, 3]));
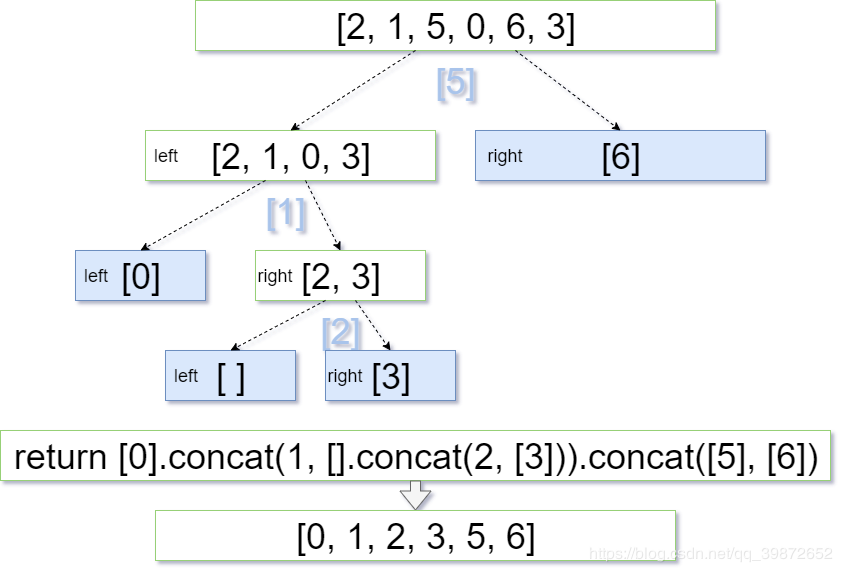
阮氏快排图解 :
阮氏快排(需要明确的点)
- 阮神的快排思路与经典的快排思路是一样的, 就是实现方式不同,阮老师是通过随机选取
主元。将数组不停的进行分割,比主元小的放在 left 数组,比主元大的放在 right 数组, - 这样一来每个递归执行的函数最后的 left pivot right都会一层一层的拼接 , 直至拼接到最外层的
quickSort(left).concat([pivot], quickSort(right)),直到最后的quickSort(right)递归完毕则完成数组的拼接,同时完成排序 - 排序过程中不断产生新数组,并且涉及删除元素再一层层向上拼接, 个人认为性能不是很好,不过好在简单容易理解, 完美的体现了快排的特点与实现思路。
经典快排
由C. A. R. Hoare在1960年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。--- 百度百科
具体原则 :
- 定义主元
- i 哨兵从左向右扫描, j 哨兵从右向左扫描。如果 i 比主元大,j 比主元小则交换位置。
- 如果二者相遇则说明相遇的这个元素就是当前区间最小元素,所以要与主元换位置
- 通过递归将数组不断分割使每个区间的主元的左边部分的所有元素小于主元, 右边部分的所有元素大于主元,这样逐渐缩小范围,最终将数组排序。
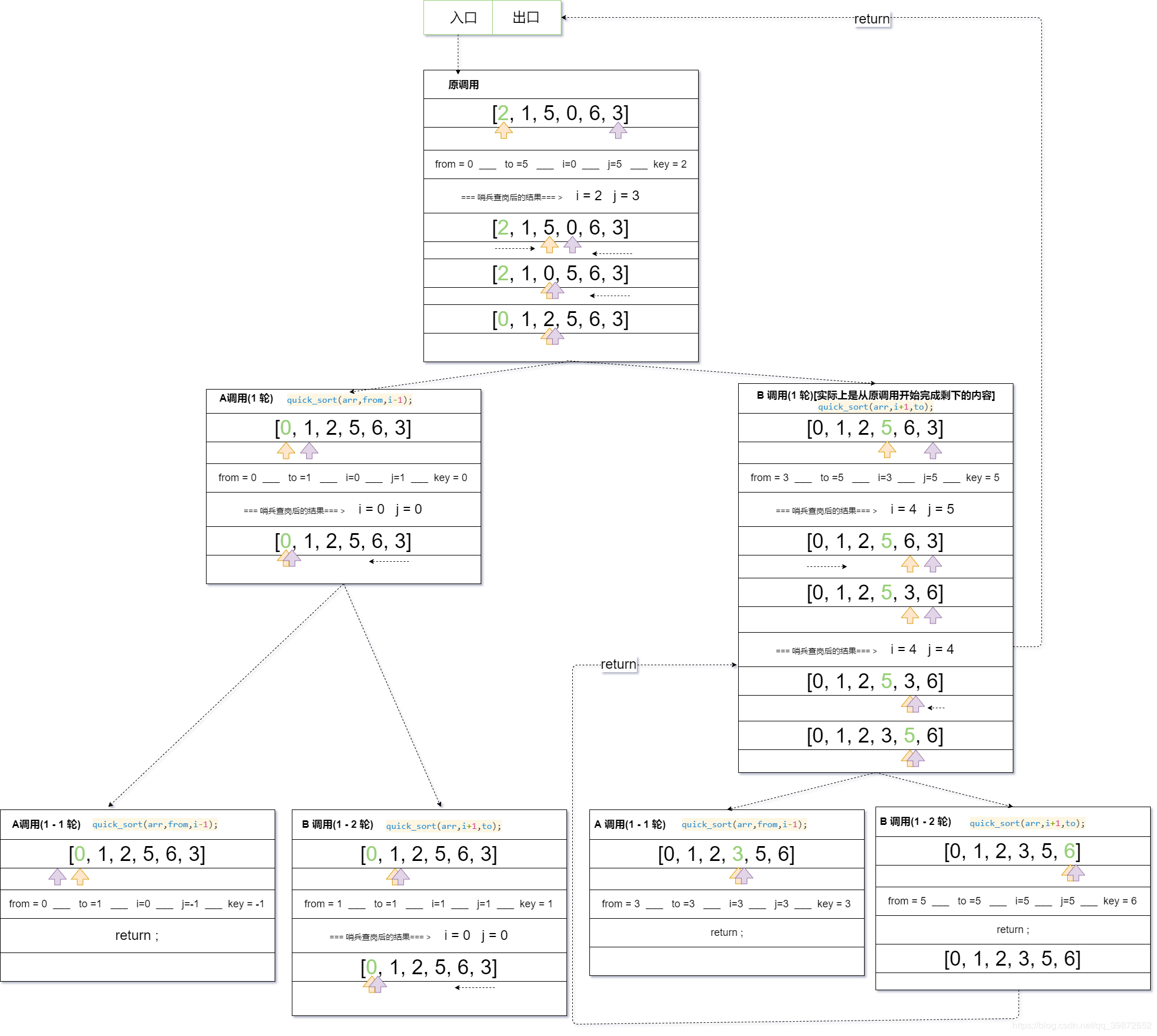
经典快排(图解原理)
经典快排(代码实现)
function quick_sort(arr,prev,next){
var i = prev; // 哨兵 i
var j = next; // 哨兵 j
var main = arr[prev]; // 标准值(主元)
if(prev>= next){ // 如果数组只有一个元素(意味着当前这部分排序完毕)
return;
}
while(i < j){
while(arr[j] >= main && i < j){ // 从右边向左找第一个比 main 小的数,找到或者两个哨兵相碰,跳出循环
j--;
}
while(arr[i] <= main && i < j){ // 从左边向右找第一个比 main 大的数,找到或者两个哨兵相碰,跳出循环
i++;
}
/**
1、两个哨兵到找到了目标值。2、j哨兵找到了目标值。3、两个哨兵都没找到( main 是当前数组最小值)
**/
if(i < j){ // 交换两个元素的位置
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
arr[prev] = arr[i] //
arr[i] = main;
quick_sort(arr,prev,i-1);
quick_sort(arr,i+1,next);
}
var arr = [2, 1, 5, 0, 6, 3];
console.log(arr);
quick_sort(arr,0,arr.length-1);
console.log(arr);
经典快排(需要明确的点)
- 整体的递归流程 : 其中
A调用(1 轮)与B 调用(1 轮)在同一级的, 只不过A调用(1 轮)先处理了两个递归子流程A调用(1 - 1 轮)、B 调用(1 - 2 轮),然后才跳出来执行B 调用(1 轮)和B 调用(1 轮)的两个递归子流程A 调用(1 - 1 轮)、B 调用(1 - 2 轮),这就是完整的排序递归流程。可以从上面的图看出,这就是"分治"思想。-
原调用后 : [0, 1, 2, 5, 6, 3]
-
A 调用排序后 : [0, 1] 2
-
B 调用排序后 : 2 [5, 6, 3]
5 [6, 3]
又分为 : [3] 5 [6]
最后数组排序完毕 : [0, 1, 2, 3, 5, 6]
-
最后借助动图来理解一下整体交换过程
由于种种原因 : [2, 1, 5, 0, 6, 3] 数组被换成了 [2, 1, 5, 1, 6, 3]。不过不耽误演示
1与0差不太多。
后记
本文仅仅是自己对上述算法的整体流程与步骤的探究而得到一些稍稍有点价值的东西, 笔者本身是个菜鸟,暂不会从设计原理及更深层次研究,而仅仅停留在知道他们是如何工作最后得到正确顺序的集合,本篇文章通过自己实验与查阅资料所得,如有错误地方还请斧正。
参考链接 :
-1). 排序-冒泡排序 - 简书
-3).冒泡排序 - 百度百科
-4). 插入排序 - 百度百科
-5). 插入排序(图解)- CSDN
-6). XXX:《面试官:阮一峰版的快速排序完全是错的》完全是错的 - 知乎
-7). 《阮一峰版快速排序完全是错的》一文是否存在事实错误?- 知乎
-8). 一篇文章让你真正了解快速排序 - segmentfault
-9). 快速排序 - 百度百科
-10). 阮一峰快速排序 - CSDN
-11). 由浅入深快速排序算法(JS实现) - 简书
-12). 坐在马桶上看算法:快速排序 - 51CTO