跳表（SkipList）数据结构介绍

jameswhale
475 阅读6分钟
原文链接： mp.weixin.qq.com
使用场景 跳表（Skiplist）是一个特殊的链表，相比一般的链表，有更高的查找效率，可比拟二叉查找树，平均期望的查找、插入、删除时间复杂度都是O(logn)，许多知名的开源软件（库）中的数据结构均采用了跳表这种数据结构。

  • Redis中的有序集合zset

  • LevelDB、RocksDB、HBase中Memtable

  • ApacheLucene中的TermDictionary、Posting List

跳表结构描述

跳表可视为水平排列（Level）、垂直排列（Tower）的位置（Position，对Entry的访问抽象）的二维集合。每个Level是一个列表Si，每个Tower包含存储连续列表中相同Entry的位置，跳表的各个位置可以通过如下方式进行遍历。

  • After(P)：返回和P在同一Level的后面的一个位置，若不存在则返回NULL。

  • Before(P)：返回和P在同一Level的前面的一个位置，若不存在则返回NULL。

  • Below(P):返回和P在同一Tower的下面的一个位置，若不存在则返回NULL。

  • Above(P)：返回和P在同一Tower的上面的一个位置，若不存在则返回NULL。

有顺序关系的多个Entry（K,V）集合M可以由跳表实现，跳表S由一系列列表{S0，S1，…，Sh}组成，其中h代表跳表的高度。每个列表Si按Key顺序存储M项的子集，并额外增加两个特殊键，分别是－∞和＋∞，其中－∞小于M中的每个键，＋∞大于M中的每个键。此外，S中的列表满足以下要求（ 不同实现版本要求会有不同）。

  1. 列表S0包含集合M的每个Entry（加上带有键－∞和＋∞的特殊Entry）。

  2. 对于i=1，…，h−1，列表Si包含（包括－∞和＋∞）列表Si−1中Entry的随机生成子集。

  3. 列表Sh只包含－∞和＋∞。

Si中的Entry是从Si-1中的Entry集合中随机选择的，对于Si-1中的每个Entry，以1/2概率来决定是否需要拷贝到Si中，我们期望S1有大约n/2个Entry，S2有大约n/4个Entry，Si 有n/2 ^i。跳表的高度h大约是logn。从一个列表到下一个列表的Entry数减半并不是跳表的强制性要求，相反借助随机函数来达成。

查找算法 

SkipSearch(k):输入：Search Key输出：最底层列表S0中的位置p, 在S0所有小于等于k的Entry集合中，p对应Entry的Key是最大的。p <-StartPosition of Swhile Below（p） ！= NULL{    p <- Below(p)             // 沿着Tower往下走    while k >= key(After(p))    {        p <- After(p)           // 沿着Level往前走    }}return pFind(k):输入：Search Key输出：对应key的位置，若没有找到则返回NULLp <-SkipSearch(K)If key(p) == K then:    return pelse then   return null
插入算法 往跳表中增加Entry44的流程：

  1. 找到底层列表（S0）中39的位置，在其后插入Entry44。

  2. 假设随机函数取值为1，接着回到38的位置，在其后插入Entry44，并和底层列表S0中的Entry44连接起来形成Entry44的Tower。

  3. 假设随机函数取值为0，则插入过程终止。

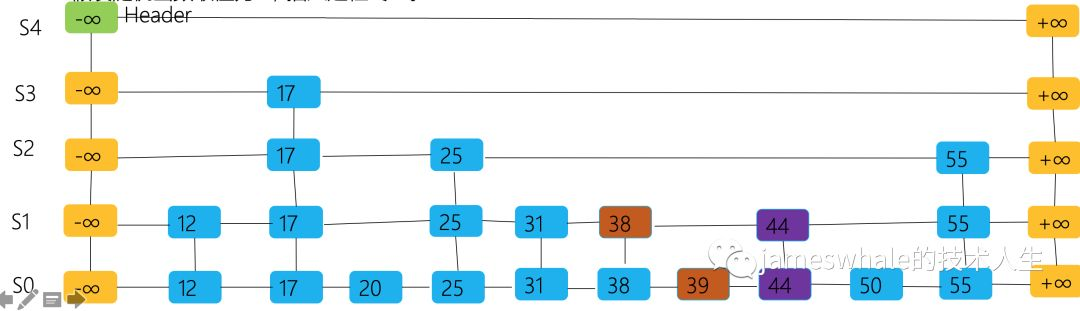
Insert(K,V):输入：K,V输出：新Entry(K,V)在这个跳表的最高位置p <-SkipSearch(K)q <- NULLe <- (K,V)i <- -1repeat    i <- i + 1    if i >= h then  // h代表跳表的高度        // 跳表增加一个Level，紧接着三句用于在新增的Level插入两个特殊Entry：(−∞, null ）， (+∞, null）        h <- h + 1         t <- After(s)  // s代表跳表的当前起始位置        s <- InsertAfterAbove(null, s, (−∞, null ))         InsertAfterAbove(s, t, (+∞, null))     //在位置p（同一Level）之后和位置q之上插入e的位置，返回e的位置    q <- InsertAfterAbove(p, q, e) // 往新Entry的Tower上面增加一个位置    while Above(p) == NULL do        p <- Before(p)  // 沿着Level往回走    p <- Above(p) // 沿着Tower往上走until random() ==0 // 0代表停止, 1代表继续。n <- n + 1   // n代表跳表的元素总数。return q
删除算法 删除Entry25的流程

找到底层列表（S0）中25的位置，并将Entry25的整个Tower删除掉。调整前后元素的指针关系。

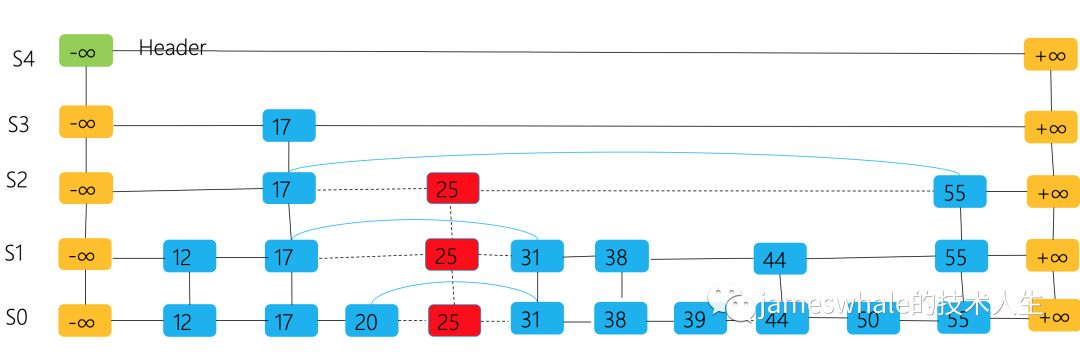
Erase(K):输入：K输出：voidp <-SkipSearch(K)// 返回跳表中底层队列S0中最大的一个小于等于K的Entry的位置。if Key(p) != K then// 没有找到对应的元素，直接返回。    returnrepeat    q <- Before(p)    r <- After(r)    modifyBeforeAfterPointer（q, r）// 调整q的后向指针和r的前向指针    temp <- p    p <- Above(p)// 沿着Tower往上走    delete tempuntil p == NULL //清除无任何数据的层t <- Below(s) // 保留最上层的-∞ 和＋∞ ，s代表跳表的起始点位置，即头结点。while t != NULL && Key(After(t)) == ＋∞  && h > 0 do     q <- t        r <- After(t)    t <- Below(t)    h <- h – 1    delete q , r

高度控制策略

跳表高度控制的策略，有如下两种：
  1. 限制最大高度：插入算法中限制跳表的最大高度，h=max{10,3* RoundUp(logn)},当超过最大高度的时候，即使随机函数值为1也不能继续在Tower上Append Entry了。边界情况，当RoundUP（logn） <RoundUp(log(n+1)),仍然可以append一次。

  2. 不限制最大高度：插入算法中不限制跳表的最大高度，以随机函数的值来确定是否继续在Tower上Append Entry。（后面会给出高度>log(n)的概率推导，概率是非常低的，所以这种方法也能Work）

时间与空间分析 最坏场景

    当每个元素的Tower的高度都是h的时候，查找、插入、删除的性能最差，为O(n+h),n为跳表的元素数目，h为跳表高度。 从这一点看，跳表没有红黑树稳定。

跳表高度推导

  1. P(Entry的Tower的高度i)= P(连续i次随机数取值为1) = 1 / 2^i，其中P代表概率， i >= 1。
  2. P(Leveli 至少有1个元素)  <= n / (2^i),n为跳表元素个数。
  3. P(跳表高度大于i) = P(Leveli至少有1个元素) 。
  4. 假设跳表高度为3logn,则P(h>3logn) <= n / (2^3logn) = 1/(n^2),假设跳表元素有1000个，则P(h > 3logn)是百万分之一，反过来，有极大概率保证跳表的高度小于等于3logn，故h = O(logn)

查找时间推导（插入、删除类似）

  1. 查找包括两个循环，外层循环是从上层Level至底层Level，内层循环是在同一个Level，从左到右。
  2. 因跳表高度以极大概率为O(logn)，所以外层循环的次数以极大概率为O(logn)。
  3. 在上层查找比对过的key，不会再下层再次查找比对，任意一个Key被查找比对的概率是1/2,因此内层循环的比对次数的期望约等于2，即O(1)。
  4. 最终查找的时间=O(1)*O(logn)，也即O(logn)。

空间占用推导

avatar
文章
阅读
粉丝