线性表
线性表定义
- 线性表L定义为:

- 线性表由n个元素组成,当n=0时,()表示为空线性表;当n>1时,表中第一个元素有唯一的后继,最后一个元素有唯一的前驱,其余元素有惟一的后继和前驱,因而呈线性关系;
线性表的操作
- 在表中查找某个元素
- 访问第i个元素,0 <= i < n
- 将新的元素赋予第i个元素,0 <= i < n
- 将新的元素插入第i个位置,0 <= i < n
- 删除第i个元素,0 <= i < n
- 计算表的长度
- 判断表是否为空
- 判断表中是否包含某个元素
线性表ADT(Abstract Data Type)
抽象数据类型ADT,一个数据结构及定义在该结构上的一组操作的总称;
package com.megvii.sun.algorithm.list;
public interface List<E> {
// 返回线性表的大小
int getSize();
// 判断线性表中是否为空
boolean isEmpty();
// 判断线性表中是否包含元素o
boolean containes(E o);
// 在线性表中查找元素o,存在返回位置index,不存在返回-1
int indexOf(E o);
// 获取线性表中位置为index中的元素
E get(int index);
// 将线性表中下标为index中的元素设置为e
void set(int index,E e);
// 在线性表中的index的位置添加元素e
void add(int index,E e);
// 删除并返回下标为index的元素
E remove(int index);
}数组
数组定义
数组是最常见的数据结构,每种编程语言中,基本都会有数组这种数据类型;其定义为用一组连续的内存空间,来存储一组具有相同数据类型的数据,支持随机访问;
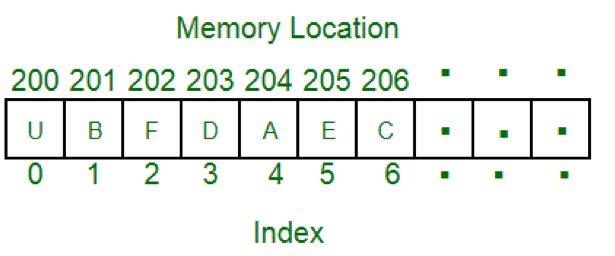
动态数组
c++中的Vector / java中的ArrayList都是属于动态数组的一种,其定义为在运行时具有改变数组大小,当添加新的元素时,容量已经等于当前的大小的时候(内存中已经存不下了):
- 重新开辟一块大小为当前容量两倍的数组
- 把原数据拷贝过去,释放掉旧的数组
链表
链表的定义
- 链表是一种物理上地址非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现
- 链表有一系列结点组成,每个节点包含两个部分,一个是存储数据元素的数据域,另一个是存储下一个节点的地址的指针域
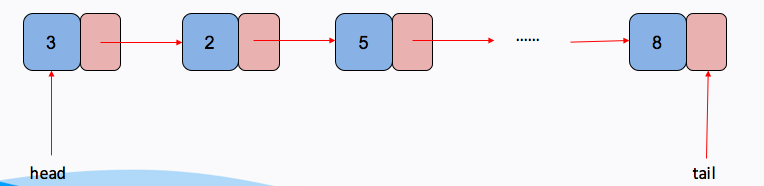
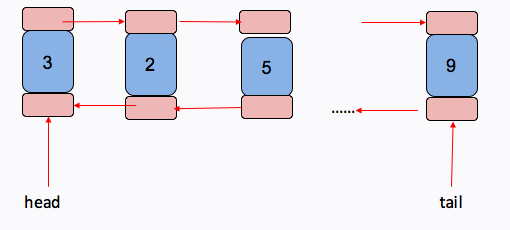
双向链表
双向循环列表是单项循环列表的每个节点中再设置一个指向前驱节点的指针域,可以进行两个方向的查找,但是插入和删除时比较麻烦;
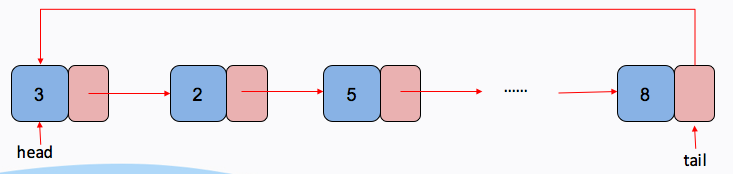
循环列表
将单链表中终端结点的指针端由空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相连的单链表称为单循环链表,简称循环链表;
- 表尾元素的next指针不为null
- 判断方式为是否等于head
- 从链表的任何一个节点都可以找到其他节点
ArrayList & LinkedList
底层实现
ArrayList是内部实现一个动态分配的数组,在没有指定List的大小时,使用默认的容量大小创建,在指定List大小后,这里使用指定的大小创建了,如果增加的元素超过size大小时,那么ArrayList底层会新生成一个数组,长度为原来数组的1.5倍+1,然后将原数组的内容复制到新的数组中,并且后续增加的内容都会放入新的数组时,当新数组无法容纳增加的元素时,重复该过程。是一旦数组超出长度,就开始扩容数组,扩容数组调用的方法 Arrays.copyOf(objArr, objArr.length + 1);
LinkedList底层实现的数据结构是基于双向链表的(JDK1.6之前使用循链表,JDK1.7取消了循环),LinkedList没有长度的概念,所以不存在容量不足的问题,因此不需要进行初始化大小的size;而且可以被当做list集合,双端队列和栈来使用;
ArrayList & LinkedList异同(扩展内容)
- 是否保证线程安全:ArrayList & LinkedList都是不同步的,也就是不能保证线程安全
- 底层数据结构的不同,上述底层实现描述已经说明
- 是否支持快速随机访问:LinkedList不支持高校快速的随机访问,但是删除、插入速度会很快,而ArrayList底层使用数组实现,能够通过get(int index)快速访问元素;
- 内存空间占用:ArrayList的空间浪费主要体现在在list列表的结尾会预留一定的容量空间,而LinkedList的空间花费则体现在它的每一个元素都需要消耗比ArrayList更多的空间(因为要存放直接后继和直接前驱以及数据)
- 插入和删除是否受元素位置的影响:ArrayList 会默认在将指定的元素追加到此列表的末尾,这种情况时间复杂度就是O(1);但是如果要在指定位置 i 插入和删除元素的话时间复杂度就为 O(n-i),因为在进行上述操作的时候集合中第 i 和第 i 个元素之后的(n-i)个元素都要执行向后位/向前移一位的操作;LinkedList采用链表存储,所以插入、删除元素时间复杂度不受元素位置的影响,都是近似O(1),而数组近似O(n)
手动实现ArrayList & LinkedList
package com.megvii.sun.algorithm.list;
import java.util.Arrays;
public class MyArrayList<E> implements List<E>{
// 定义初始化数组大小
private static final int DEFAULT_CAPACITY = 10;
// 定义初始化数组,存放元素
private E[] data;
// 定义初始化size,记录目前有多少元素
private int size;
/**
* 默认构造方法
*/
public MyArrayList(){
this(DEFAULT_CAPACITY);
}
public MyArrayList(int capacity){
if(capacity < 0){
throw new IllegalArgumentException("数组容量不能为负....");
}
data = (E[])new Object[capacity];
size = 0;
}
@Override
public int getSize() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean containes(E o) {
for (int i = 0;i < size;i++){
if(data[i].equals(o)){
return true;
}
}
return false;
}
@Override
public int indexOf(E o) {
for (int i = 0; i < size; i++) {
if(data[i].equals(o)){
return i;
}
}
return -1;
}
@Override
public E get(int index) {
if(index < 0 || index >= size){
throw new IllegalArgumentException("数组下标越界....");
}
return data[index];
}
@Override
public void set(int index, E e) {
if(index < 0 || index >= size){
throw new IllegalArgumentException("数组下标越界....");
}
data[index] = e;
}
@Override
public void add(int index, E e) {
if(index < 0 || index > size){
throw new IllegalArgumentException("数组下标越界....");
}
// 数组扩容
if(size == data.length){
grow(DEFAULT_CAPACITY * 2);
}
// 数据后移动
for(int i = size - 1;i >= index; i--){
data[i + 1] = data[i];
}
data[index] = e;
size ++;
}
private void grow(int newCapacity){
data = Arrays.copyOf(data,newCapacity);
}
@Override
public E remove(int index) {
if(index < 0 || index >= size){
throw new IllegalArgumentException("数组下标越界....");
}
E val = data[index];
// 删除之后从删除的元素之后向前移动
for(int i = index + 1;i < size;i++){
data[i -1] = data[i];
}
// 缩容
if(size < data.length / 2){
grow(data.length / 2);
}
size --;
return val;
}
}
package com.megvii.sun.algorithm.list;
public class MyLinkedList<E> implements List<E> {
/**
* 节点定义
* @return
*/
private class Node{
// 数据域
private E data;
// 指针域,指向下一个Node
private Node next;
public Node(E data, Node next) {
this.data = data;
this.next = next;
}
public Node(E data){
this(data,null);
}
}
// 定义头部节点
private Node head;
// 定义size
private int size;
public MyLinkedList(){
head = null;
size = 0;
}
@Override
public int getSize() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean containes(E o) {
Node p = head;
while (p != null) {
if(p.data.equals(o)){
return true;
}
p = p.next;
}
return false;
}
@Override
public int indexOf(E o) {
int result = 0;
Node p = head;
int i = 0;
while(p != null){
if(p.data.equals(o)){
result = i;
}
p = p.next;
i ++;
}
return result;
}
@Override
public E get(int index) {
// 考虑数组下标越界问题
if(index < 0 || index >= size){
throw new IllegalArgumentException("数组下标越界....");
}
Node p = head;
for (int i = 0; i < index; i++) {
p = p.next;
}
return p.data;
}
@Override
public void set(int index, E e) {
// 考虑数组下标越界问题
if(index < 0 || index >= size){
throw new IllegalArgumentException("数组下标越界....");
}
Node p = head;
for (int i = 0; i < size; i++) {
p = p.next;
}
p.data = e;
}
@Override
public void add(int index, E e) {
if(index < 0 || index > size){
throw new IllegalArgumentException("数组下标越界....");
}
// 插入到链表头部
if(index == 0){
Node node = new Node(e,head);
head = node;
size ++;
}else if(index == size){ // 插入到链表尾部
Node node = new Node(e, null);
//链表为空
if(head == null) {
head = node;
}else {
Node prev = head;
while(prev.next != null) {
prev = prev.next;
}
prev.next = node;
}
size++;
}else{
Node prev = head;
for(int i=0; i<index; i++) {
prev = prev.next;
}
prev.next = new Node(e, prev.next);
size++;
}
}
@Override
public E remove(int index) {
if(index < 0 || index >= size) {
throw new IllegalArgumentException("非法下标...");
}
if(index == 0) {
return removeFirst();
}else if (index == size - 1) {
return removeLast();
}else{
Node prev = head;
for(int i = 0; i < index - 1; i++){
prev = prev.next;
}
Node tmp = prev.next;
prev.next = tmp.next;
tmp.next = null;
size--;
return tmp.data;
}
}
public E removeFirst() {
if(head == null){
return null;
}
E result = head.data;
head = head.next;
size --;
return result;
}
public E removeLast() {
if(head == null)
return null;
E result;
//链表只有一个节点
if(head.next == null) {
result = head.data;
head = null;
}else {
Node prev = head;
while(prev.next.next != null){
prev = prev.next;
}
result = prev.next.data;
prev.next = null;
}
size--;
return result;
}
}