描述
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
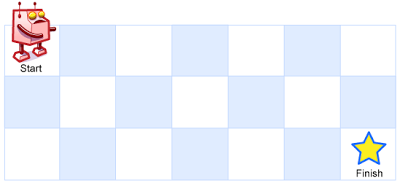
Above is a 7 x 3 grid. How many possible unique paths are there?
Example 1:
Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> RightExample 2:
Input: m = 7, n = 3
Output: 28Constraints:
1 <= m, n <= 100
It's guaranteed that the answer will be less than or equal to 2 * 10 ^ 9.思路
在知乎上学到了动态规划的基本知识,就找了这道题作为练习巩固。
此题以棋盘为dp数组的形象描述,有助于初学者进行理解。
- 除第一行及第一列的格子只有一种到达方式外,其他的格子需要从左边/上边的格子读取上一个状态,并将这两个状态相加,得到最右下角的路径数。
关系式是 dp[i][j] = dp[i-1][j] + dp[i][j-1]
class Solution {
public int uniquePaths(int m, int n) {
int dp[][] = new int[m][n];
for(int i = 0; i<n; i++){
dp[0][i] = 1;
}
for(int i = 0; i<m; i++){
dp[i][0] = 1;
}
for(int i = 1; i<m; i++){
for(int j = 1; j<n; j++){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
}优化
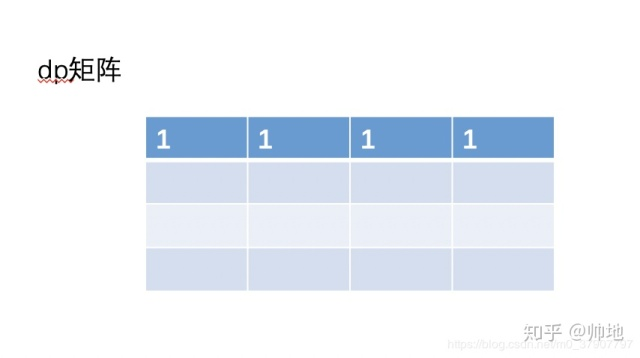
根据上一行的数值及第一列的数值(恒为1)计算第二行(下图)
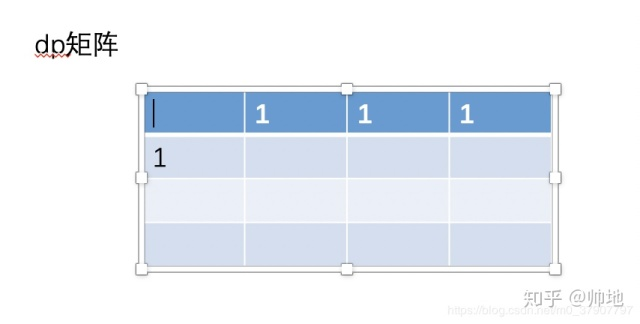
计算过程(下图*3)
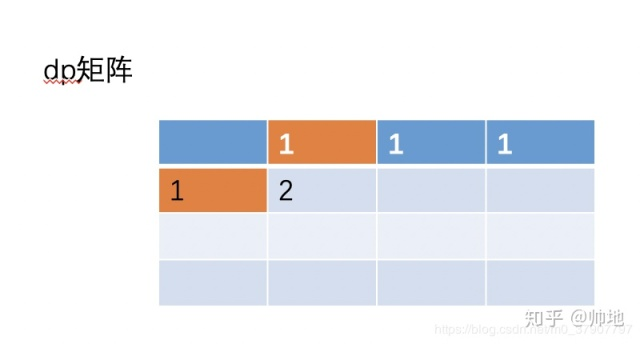
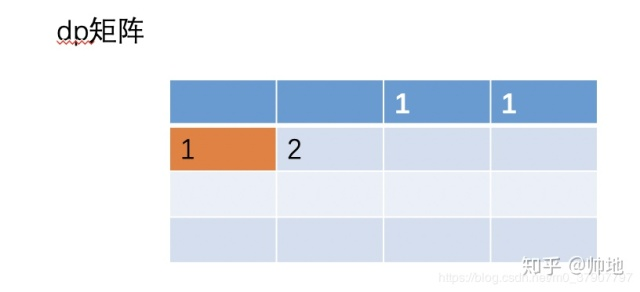
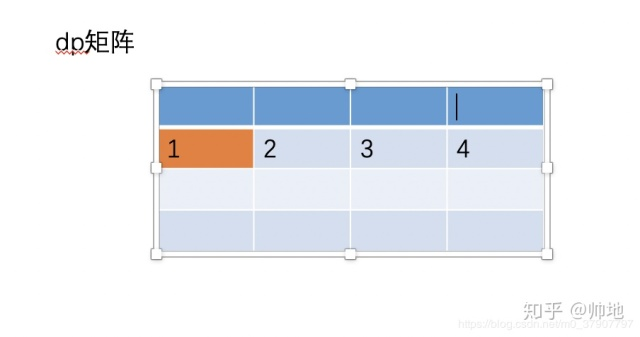
可以观察到,第i行j列的数据生成之后,第i-1行j列的数据就可以不用保存了。即满足关系式dp[i] = dp[i-1] + dp[i]。照此推理过程不难推出最后一行的情况(下图)
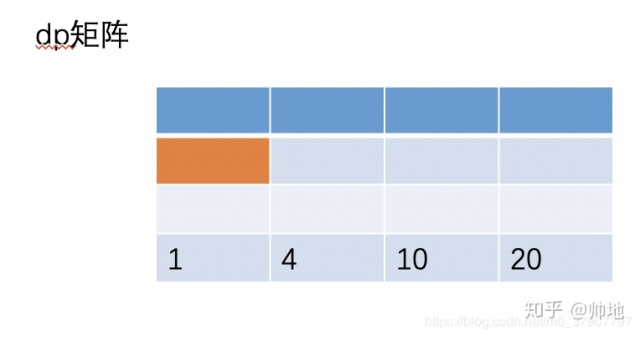
右下角即为所求。
class Solution {
public int uniquePaths(int m, int n) {
int dp[] = new int[n];
for(int i = 0; i<m; i++){
dp[0] = 1;
for(int j = 1; j<n; j++){
dp[j] = dp[j-1] + dp[j];
}
}
return dp[n-1];
}
}数学优化(来自LeetCode题目评论区)
The total number of movements of the robot is S=m+n-2, and the number of
downward movements is D=m-1. Then the problem can be seen as the number
of combinations of D positions taken from S. The solution to this
problem is C(S, D).
class Solution(object):
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
return math.factorial(m+n-2)/math.factorial(m-1)/math.factorial(n-1)使用数学组合方法进行计算,空间复杂度O(1)。