一、前言

各种排序算法的掌握对于一个程序猿来说还是有必要掌握的, 所以自己打算对各种排序算法都分析一遍，首先从堆排序开刀。

二、基本思想

堆的定义如下:n个元素的序列{ $k_1$ , $k_2$ , $\ldots$ , $k_n$ }, 当且仅当满足下列关系时，称之为堆:

\begin{cases}
k_i \leq k_{2i}, \\
k_i \leq k_{2i+1}, \\
\end{cases}

或

\begin{cases}
k_i \geq k_{2i}, \\
k_i \geq k_{2i+1}, \\
\end{cases}

其中，第一种被称做小顶堆，第二种被称做大顶堆。他们的区别就是最顶上的数是最大值还是最小值。值得注意的是，堆只规定了父节点比子结点大或者小，并没有规定左子结点必须比右字节的大或者小。那么堆排序是什么呢？如果我们在输出堆顶的最大/最小值之后，使得剩余的n-1个元素的序列又重键成一个堆，则得到n个元素中的次大/小值。如此反复执行，便可以得到一个有序序列，这个过程被称为堆排序。那么问题就简单了，我们现在需要解决两个问题就可以实现堆排序:

把一个无序数组建成堆
输出堆顶元素后将剩余元素调整为一个新的堆

其实，这两个问题又可以看成一个问题，为什么呢？首先我们先思考第二个方法如何实现，在这里我们以最小堆为例:我们输出堆顶值之后，堆顶值的左右均为最小堆，我们只需要找出左右结点中比较小的那一个去和堆顶值比较，此时有两种情况:

结点中比较小的值仍然比堆顶元素大，即堆顶元素是最小值，此时不需要调整
结点中比较小的值比堆顶元素大(假设是左结点)，需要将其与堆顶元素交换位置，同时左子树的堆受到影响，使用递归继续调整，右子树不受影响，无需调整。

可以看出，我们使用这个方法的基本条件就是:当前结点的左右均为已经调整好的堆，这样我们就能使用递归去将其重新调整为一个新的堆。那么如果只有三个结点，父结点，两个子结点，两个子结点一定是两个堆，因为它根本没有子结点。分析到这里，我们可以得出一个结论:我们可以利用第二个方法，去找无序数组中第一个非叶结点，然后从该结点往根结点，依次调用adjust方法，将无序数组调整为堆。如果不理解这句话，那么从图来看比较直观：

1方框的父结点是第一个非叶结点，我们从它开始，对每个红色方框内的结点调用adjust方法，当所有红色方框都调用过这个方法后，所有红色方框都会变成堆。此时，5，6方框就符合当前左右结点均为已经调整好的堆这条规则了，可以继续使用adjust方法，同理，调整好绿色方框后，我们可以继续往上找，直到根结点，这样，就将无序数组调整为了堆。这样，只要我们解决了第二个问题，第一个问题也就迎刃而解了。

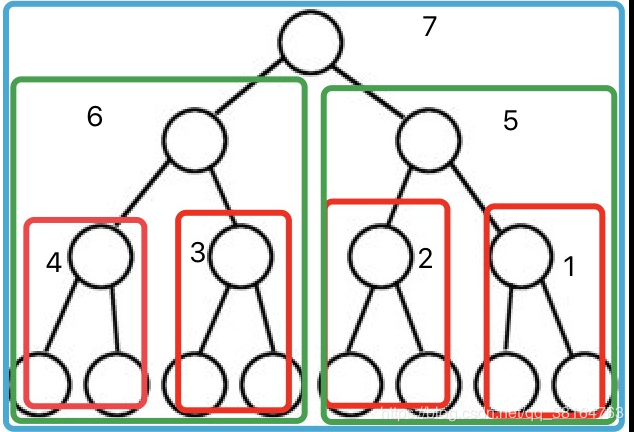
三、adjust方法的实现

我们的函数接受三个参数，第一个就是当前的数组，第二个是开始结点下标和结束结点下标，这里我们数组的第一个元素下标是0，所以我们可以得到，当前结点的左结点的下标是 $2n+1$ ，而右结点的下标是 $2n+2$ 。得到结点下标后，我们需要判断一下左结点的下标是否已经超出结束结点下标，如果超过意味着这个结点是叶结点，不需要继续调整了。如果没有超过，我们拿到左右结点的值，这里有一个注意的地方是此时还要考虑右结点是否存在，如果不存在我们给他一个正无穷的值。最后就是找出最小结点来和父结点进行比较并递归调整左/右子树。具体代码如下:

    function adjustHead(arr, beg, end) {
        const left = beg*2+1, right = beg*2+2;
        if(left > end) {
            return ;
        }
        const leftVal = arr[left], rightVal = right <= end ? arr[right] : Infinity, nowVal = arr[beg];
        if(leftVal < nowVal && leftVal < rightVal) {
            [arr[left], arr[beg]] = [arr[beg], arr[left]];
            adjustHead(arr, left, end);
        }else if(rightVal < nowVal && rightVal < leftVal) {
            [arr[right], arr[beg]] = [arr[beg], arr[right]];
            adjustHead(arr, right, end);
        }
    }

四、将无序数组调整为最小堆

根据我们之前的分析，这个问题应该很好解决。此时我们只需要解决一个问题，如何找到第一个非叶结点。我们可以知道，这个结点肯定是倒数第二层的最后一个结点，此时从该结点到根结点一共有 $2^{k-1}-1$ 个结点，而最后一层有 $2^{k-1}$ 个结点，所以其实我们要找的那个结点的坐标就是 $\lfloor n/2 \rfloor$ ，那么调整的代码就很简单了:

	let length = arr.length;
    for(let i = parseInt(length/2); i>=0; i--) {
        adjustHead(arr, i, length-1);
    }

五、完整堆排序

我们最后每次只需要取堆顶元素放到末尾，再对剩下的元素进行调整，就完成了我们的堆排序

function headSort(arr) {
    let length = arr.length;
    for(let i = parseInt(length/2); i>=0; i--) {
        adjustHead(arr, i, length-1);
    }
    for(let i = 0; i < length - 1; i++) {
        [arr[0], arr[length - i -1]] = [arr[length - i - 1], arr[0]];
        adjustHead(arr, 0, length - i - 2);
    }
    function adjustHead(arr, beg, end) {
        const left = beg*2+1, right = beg*2+2;
        if(left > end) {
            return ;
        }
        const leftVal = arr[left], rightVal = right <= end ? arr[right] : Infinity, nowVal = arr[beg];
        if(leftVal < nowVal && leftVal < rightVal) {
            [arr[left], arr[beg]] = [arr[beg], arr[left]];
            adjustHead(arr, left, end);
        }else if(rightVal < nowVal && rightVal < leftVal) {
            [arr[right], arr[beg]] = [arr[beg], arr[right]];
            adjustHead(arr, right, end);
        }
    }
}

let arr = [2, 3, 5, 3, 7, 8, 23, 11, 15]
headSort(arr);
console.log(arr);
//[ 23, 15, 11, 8, 7, 5, 3, 3, 2 ]

六、时间复杂度分析

如果你仔细了阅读了本篇文章，就能感觉到我们最核心的算法就是adjusetHeap调整函数，我们先来分析一下这个函数的时间复杂度。如果从第i层开始调整，那么最坏的情况就是从该层需要一直调整到最末层，即需要做h-i次调整操作，其中还包含比较操作，但是是常数级别，可以忽略，所以时间复杂度为 $O(h-i)$ ，其中h为整颗树的高度。那么下面我们可以分成几个部分来分析整个算法的时间复杂度

建堆时候的时间复杂度: 我们从倒数第二层开始，对最后一个非叶结点到根结点的每个结点都调用了adjustHeap函数，假设一共有 $h$ 层，第 $h-1$ 层有 $2^{h-1-1}$ 个结点，所以该层的结点总共的操作次数是 $2^{h-1-1}*(h - (h - 1))$ ， $h-2$ 层的操作次数是 $2^{h-2-1}*(h - (h - 2))$ ，第h-1层到第1层总共的操作次数是

S = 2^{h-1-1}*(h - (h - 1)) + 2^{h-2-1}*(h - (h - 2)) + \ldots + 2^{1-1}*(h-1)

化简一下为:

S = 2^{h-2}*(1) + 2^{h-3}*(2) + \ldots + 2^{1}*(h-2) +2^{0}*(h-1)

这里我们需要用一点数学的小技巧，将该等式整体乘 $2$ ，得到下面的式子:

2S = 2^{h-1}*(1) + 2^{h-2}*(2) + \ldots + 2^{1}*(h-1)

再用式2减去式1，得到

S = 2^{h-1} + 2^{h-2} + 2^{h-3} + \ldots + 2 - (h-1)

这是一个我们非常熟悉的等比数列求和，套用公式得出最后的结果是: $2^h-h-1$ 。同时，h是树的高度，所以有 $h = \lfloor log_2n \rfloor + 1$ ，我们将其近似为 $log_2n$ ，所以代入式子后得到:

所以建堆的时间复杂度为 $O(n)$ 。

调整时的时间复杂度调整时我们值调用了adjustHeap函数，假设此时树的高度为h，那么时间复杂度就是 $O(log_2h)$
排序时的时间复杂度我们排序做的操作是，将堆顶元素替换掉，然后对其进行调整，由上面的分析可知，我们一共需要进行 $n$ 次操作，为了方便计算，我们假设树的高度不变，为 $log_2n$ ，所以时间复杂度就为 $nlog_2n$ 。

所以堆排序的时间复杂度为 $n+nlog_2n$ ，即 $nlog_2n$

七、结语

通过分析我们可以看出，堆排序中利用了递归去实现，所以对于数据量比较小的排序，我们可以采取其他方法，比如冒泡，直接插入排序等，性能会比堆排序好。同时因为大多数排序的最坏情况时间复杂度为 $n^2$ ，当数据量比较大时， $n^2$ 和 $nlog_2n$ 差异较大，所以堆排序在大数据排序上的表现应该要比小数据量排序好。最后，对于Topk问题，我们也可以采用建立一个最小堆的方法，这样不用将全部数据读入内存，只需要维护这个堆，最后留在堆中的即为前k大的数据。

经典排序算法之堆排序