一、凸集的定义[1]
定义:设为
维欧式空间
中的一个集合,若对
中任意两点,联结他们的线段仍属于
;换言之,对
中任意两点
,
,及每个实数
[0,1],都有
则称为凸集。如图1:
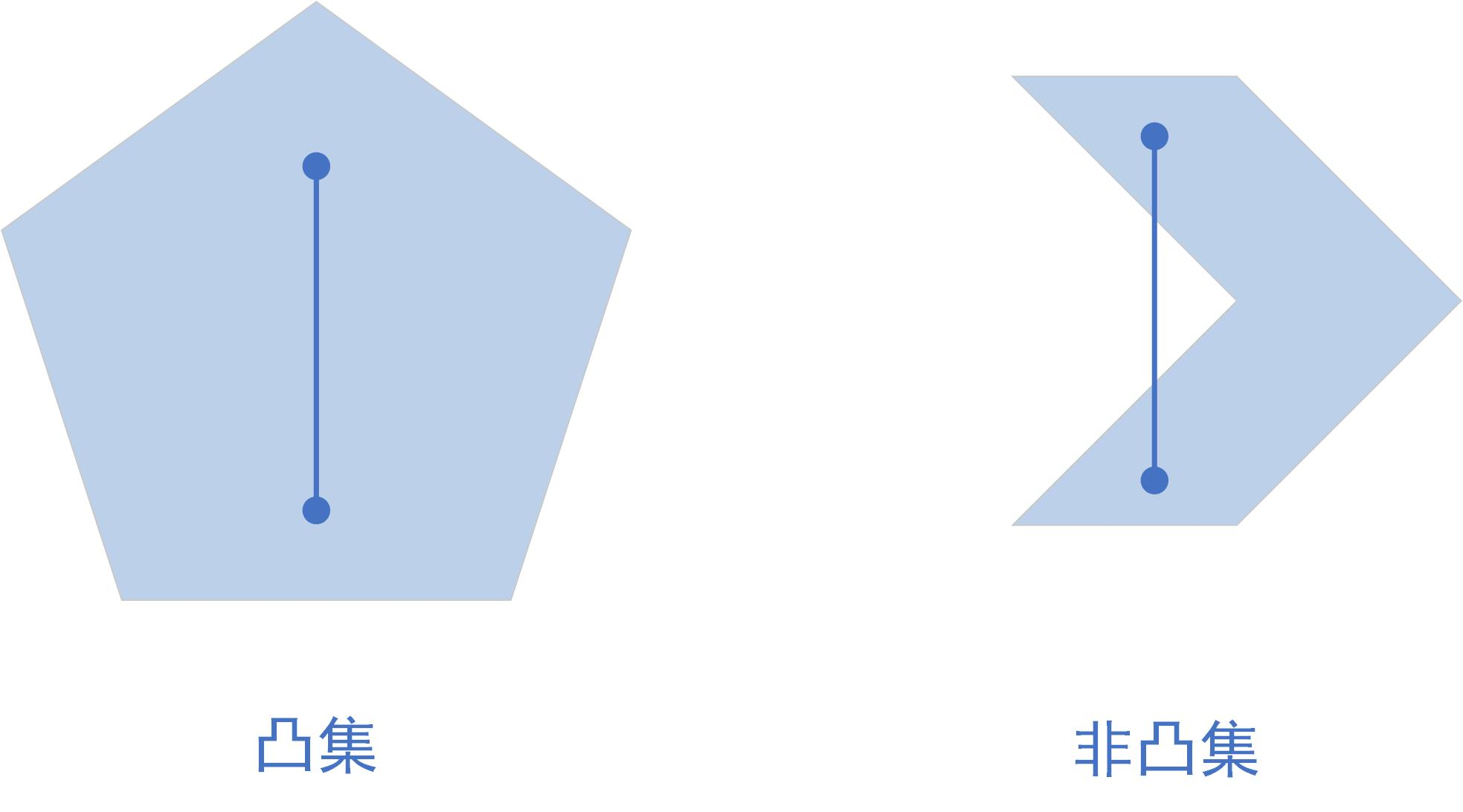
二、凸集定义直观理解
为什么公式(1)的前半部分
能表示两个点的联线?把公式(2)展开并合并含有项得到
几何图形具有直观理解的好处,我们在几何图形中表示公式(3),并进行理解,请看图2:
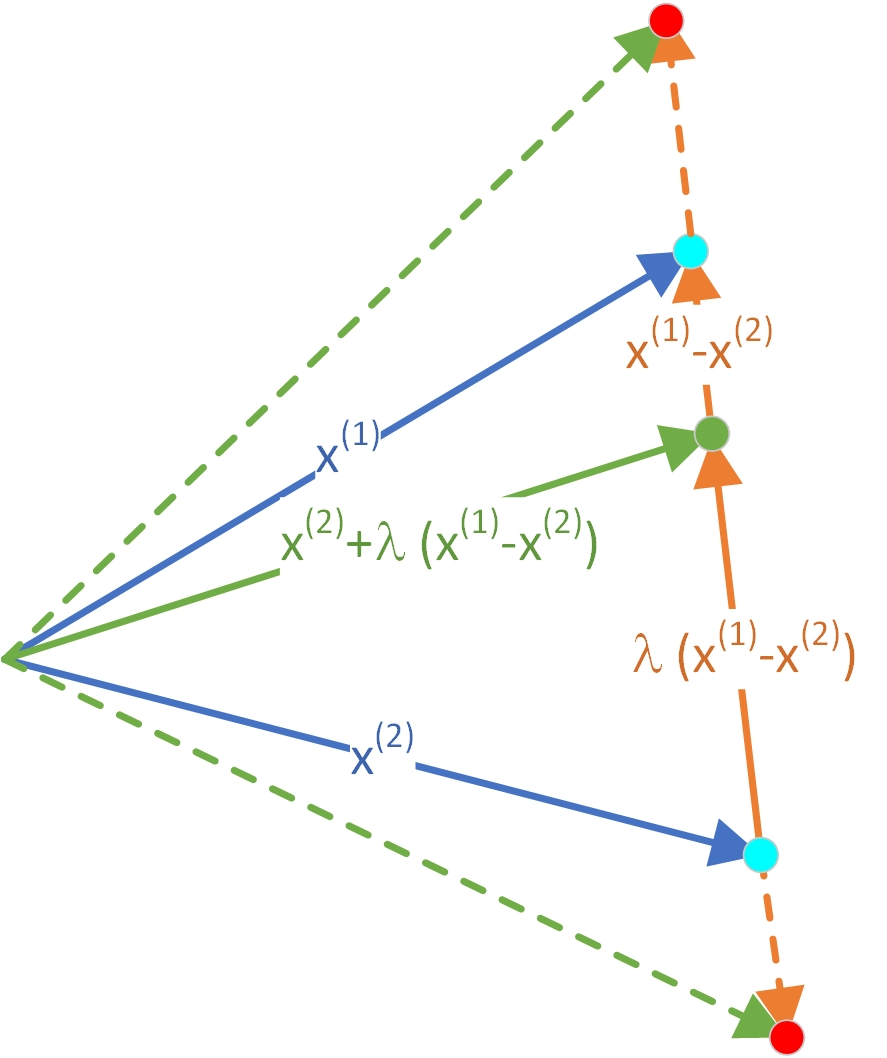
短黄色实线向量表示当时
所以公式(3)可以表示为绿色实线向量,其终点在和
的联结线段上;但当
时,其终点在联结直线上,但在线段外,两个红色点分别表示当
和
时,其终点的位置。
陈宝林.最优化理论与算法(第2版)[M].清华大学出版社:北京,2015:10. ↩︎