动态规划中包含3个重要的概念：

最优子结构
边界
状态转移公式。以爬楼梯为例，最优子结构为 $f(10) = f(9) + f(8)$ ，边界是 $f(1) = 1, f(2) = 2$ ，状态转移公式 $f(n) = f(n-1) + f(n-2)$

斐波那契数列

70. 爬楼梯

本质上为斐波那契数列。递归会超时（python 可设置缓存，不会超时），要用动态规划或直接应用通项公式

定义一个数组 $dp$ 存储上楼梯的方法数（为了方便讨论，数组下标从 $1$ 开始）， $dp[i]$ 表示走到第 $i$ 个台阶的方法数目。
第 $i$ 个台阶可以从第 $i - 1$ 和 $i - 2$ 个台阶再走一次到达，走到第 $i$ 个台阶的方法数为走到第 $i - 1$ 和第 $i - 2$ 个楼梯的方法数之和。

198. 打家劫舍

定义 $dp$ 数组用来存储最大的抢劫量，其中 $dp[i]$ 表示抢到第 $i$ 个住户时的最大抢劫量。
由于不能抢劫邻近住户，如果抢劫了第 $i - 1$ 个住户，那么就不能再抢劫第 $i$ 个住户，所以： $dp[i] = \max (dp[i - 2]+nums[i], dp[i - 1])$

衍生题：环形街区
取 $[1, n]$ 和 $[0, n - 1]$ 两者的最大值

矩阵路径

62. 不同路径

排列组合

多重集排列问题

路径方向为多重集，有 向右 和 向下 两种（方向）元素，两种元素的重数分别为 $n_{1}$ 和 $n_{2}$ ，有 $n = n_{1} + n_{2}$ ，则排列数为 $\left(\begin{array}{l}{n} \cr {n_{1}} & {n_{2}}\end{array}\right) = \frac{n!}{n_{1}!n_{2}!}$

⭐动态规划

令 $dp[i][j]$ 是到达 $i, j$ 的路径数，有 $dp[i][j] = dp[i-1][j] + dp[i][j-1]$

数组区间

303. 区域和检索 - 数组不可变

求数组区间 $(i, j)$ 的和

题中强调：会多次调用 sumRange 方法
因此预先求出所有 $(0, k)$ 的和，再 sum[j] - sum[i - 1]

413. 等差数列划分

等差数列满足：至少有 3 个元素、任意两个相邻（隔开不算）元素之差相同

暴力

每一对元素（之间至少隔着一个元素），根据两个元素之间的所有元素差值是否相等来判断是不是等差数列

💣动态规划（想不到这方法）

$dp[i]$ 表示以 $A[i]$ 为结尾（不是总的）的等差递增子区间的个数，对于 $A = [0, 1, 2, 3, 4]$ ，有以下结论：

dp[2] = 1
    [0, 1, 2]
dp[3] = dp[2] + 1 = 2
    [0, 1, 2, 3], // [0, 1, 2] 之后加一个 3
    [1, 2, 3]     // 新的递增子区间
dp[4] = dp[3] + 1 = 3
    [0, 1, 2, 3, 4], // [0, 1, 2, 3] 之后加一个 4
    [1, 2, 3, 4],    // [1, 2, 3] 之后加一个 4
    [2, 3, 4]        // 新的递增子区间

综上，在 A[i] - A[i-1] == A[i-1] - A[i-2] 时，dp[i] = dp[i-1] + 1

这里的 $dp[i]$ 不是最终的结果，而是每步的结果。思考的时候过于死板

⭐分割整数

343. 整数拆分

没思路

贪心思想（举例得出规律）

数字 $n$ 可由 $a$ 个 $x$ 和 $1$ 个 $b$ 相加而成。是否有优先级最高的因子 $x$ 存在，有以下判断：

$2 = 1 + 1$ ， $1 * 1 < 2$ ，因此 $2$ 比 $1 + 1$ 更优；
$3 = 1 + 2$ ， $1 * 2 < 3$ ，因此 $3$ 比 $1$ 和 $2$ 更优；
$4 = 2 + 2$ ， $2 * 2 = 4$ ，因此可以认为 $4$ 与 $2$ 等价，因此见到 $4$ 就拆分；
$5 = 2 + 3$ ；因为每个 $5$ 都可以拆分为 $2+3$ ，而 $2 * 3 = 6 > 5$ ，因此见到 $5$ 就拆分。
$6 = 3 + 3 = 2 + 2 + 2$ ；因为 $3 * 3 > 2 * 2 * 2 > 6$ 。因此见到 $6$ 就拆分，并且 $3$ 是比 $2$ 更优的因子。

易推出：大数字都可以被拆分为多个小因子，以获取更大的乘积，只有 $2$ 和 $3$ 不需要拆分。列出以下贪心法则：

第一优先级：；把数字拆成尽可能多的之和；
- 特殊情况：拆完后，如果余数是 $1$ ；则应把最后的 $3 + 1$ 替换为 $2 + 2$ ，因为后者乘积更大；
第二优先级： $2$ ；留下的余数如果是 $2$ ，则保留，不再拆为 $1+1$

当 $n <= 3$ 时，直接返回 $n - 1$

动态规划

$dp[i]$ 表示：数字 $i$ 拆分为至少两个正整数之和的最大乘积。
有转移方程： $dp[i] = \max (dp[i], j * dp[i - j])$
由于 $i - j <= 3$ 时， $dp[i - j] = i - j - 1 < i - j$ ，所以 $dp[i] = \max (dp[i], j * \max(dp[i - j], i - j))$

279. 完全平方数

BFS

前面有做过

动态规划

$dp[i]$ 表示：数字 $i$ 拆分为完全平方数的最少个数。
有转移方程： $dp[i] = \min (dp[i], dp[i - square] + 1), square = 1, 4, 9... <= i$

💣91. 解码方法

字符串中可能包含 "0"，因此情况比较复杂

若 s[i] == "0"
- 若 s[i - 1] = "1" or "2"，则 $dp[i] = dp[i - 2]$
- 否则，return 0
若 s[i] != "0"
- 若 s[i - 1] == "1"，则 $dp[i] = dp[i - 1] + dp[i - 2]$
- 若 s[i - 1] == "2" and "1" <= s[i] <= "6"，则
  - 解释： s[i - 1] 与 s[i] 分开译码，为 $dp[i - 1]$ ；合并译码，为 $dp[i - 2]$
- 否则，
  - 解释：此时若合并译码，则大于 $26$ ，s[i - 1] 与 s[i] 只能分开译码

最长递增子序列

300. 最长上升子序列

动态规划

$dp[i]$ 表示以 $S_i$ 结尾的序列的最长递增子序列长度。对于每个 $i$ ，向前遍历以寻找递增子序列

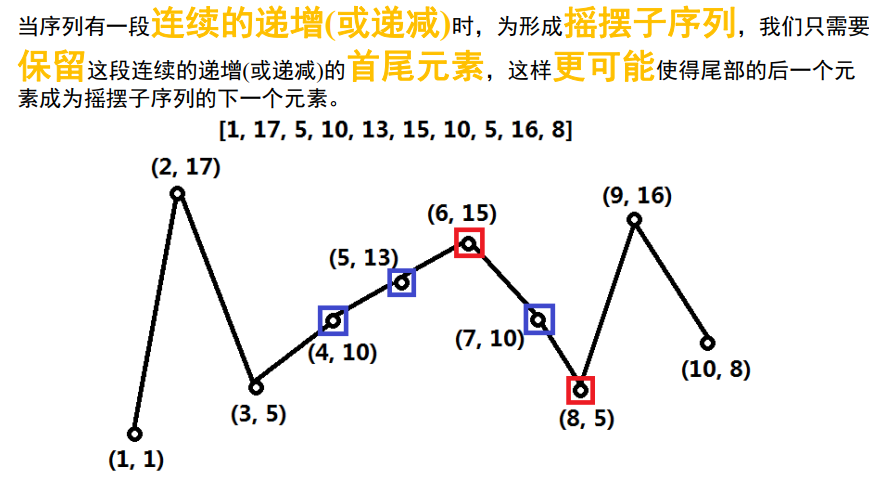
⭐376. 摆动序列

动态规划

用两个 $dp[i]$ 数组。 $up[i]$ 表示前 $i$ 个元素中摆动序列以上升元素结尾的最长子序列长度； $down[i]$ 反之。

若第 $i$ 个元素上升就更新 $up[i]$ ，如下代码：（ $down[i]$ 同理）

if (nums[i] > nums[j]) {
  up[i] = Math.max(up[i], down[j] + 1);
}

贪心算法

最长公共子序列

二维数组 $dp$ 用来存储最长公共子序列的长度，其中 $dp[i][j]$ 表示 $S1$ 的前 $i$ 个字符与 $S2$ 的前 $j$ 个字符最长公共子序列的长度，状态转移方程：

$d p[i][j]=\left\lbrace\begin{array}{ll} dp[i-1][j-1]+1 && S1_{i} == S2_{j} \cr \max (dp[i-1][j], dp[i][j-1]) && S1_{i} != S2_{j} \end{array}\right.$

特别需要注意的是，当 $S1_{i} != S2_{j}$ 时， $dp[i][j] != dp[i-1][j-1]$ 。比如：abcd 和 adbc 当 $i$ 和 $j$ 为 $4$ 时，若用错误的表达式，则最长公共子序列为 $2$

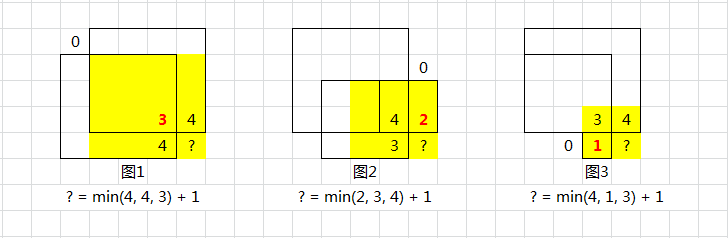
⭐221. 最大正方形

这个转移方程想不到

转移方程： ${dp}(i, j)=\min ({dp}(i-1, j), {dp}(i-1, j-1), {dp}(i, j-1))+1$
若某格子值为 1 ，则以此为右下角的正方形的、最大边长为：上面的正方形、左面的正方形或左上的正方形中，最小的那个，再加上此格。

⭐0 - 1 背包（难）

此类问题的特点：一般都有选或不选两种选择

不能使用贪心算法

令 $dp[i][v]$ 表示前 $i$ 件物品 $(1 ≤ i ≤ n, 0 ≤ v ≤ V)$ 恰好装入容量为 $v$ 的背包中所能获得的最大价值。① 第 $i$ 件物品不放入 ② 第 $i$ 件物品放入
状态转移方程： ${dp}[{i}][{v}]=\max \{{d} {p}[{i}-1][{v}], {d} {p}[{i}-1][{v}-{w}[{i}]]+{c}[{i}]\}$
$\quad(1 \leqslant {i} \leqslant {n}, {w}[{i}] \leqslant {v} \leqslant {V})$