问题描述
给定一个区间[a, b],每次生成一个该区间内的均匀分布的随机数,当生成的所有随机数之和大于c时,停止生成随机数并记下已产生的随机数的个数,问平均生成了多少个随机数?
代码实现
1. 使用 for 循环
f <- function(a, b, c)
{
count = rep(0, 1e7)
for (i in 1:length(count)) # 进行1e7次模拟
{
sum <- runif(1, a, b) # 存储已经产生的随机数个数
k <- 1
repeat
{
if (sum > c) # 若随机数之和大于目标数c,则返回随机数个数
{
count[i] <- k
break
}
else # 若随机数之和不大于目标数c,则继续生成随机数
{
sum <- sum + runif(1, a, b)
k <- k + 1
}
}
}
mean(count)
}
system.time(f(0, 1, 1))
运行结果:
> system.time(f(0, 1, 1))
用户 系统 流逝
50.37 0.02 50.65
2. 使用递归
f <- function(a, b, c, rep_count=1e7)
{
ans <- c - runif(rep_count, a, b) # 一次性生成1e7个随机数,同时操作
g <- ans > 0
if (all(!g))
{
return(g)
}
g[g] <- f(a, b, ans[g], sum(g)) # 相当于将目标数减小为ans[g]
g + 1
}
sapply(1:5, FUN=function(x){mean(f(0, 1, x))})
system.time(mean(f(0, 1, 1)))
运行结果:
> sapply(1:5, FUN=function(x){mean(f(0, 1, x))})
[1] 2.718686 4.671420 6.667014 8.667860 10.665704
> system.time(mean(f(0, 1, 1)))
用户 系统 流逝
1.48 0.13 1.62
可见:当无法确定何时终止 for 循环时,为避免 for 循环的低效率,可以采用递归向量化,从而加快运算速度。
3. 避免不必要的递归
还有改进的地方吗?
仔细分析,可以发现,随机数只在区间 [a, b] 之间产生,也就是说每一次产生的随机数不大于b,当c >> b时,前几次产生的随机数之和可能根本不会超过c,这几次的递归其实是不必要的,因此再次优化:
f_new <- function(a, b, c, rep_count=1e7)
{
n <- floor(c/b) # 计算多余的递归步数
c <- c - colSums(matrix(runif(rep_count * n, a, b), n, rep_count)) # 直接累加前几次的随机数
f_in <- function(a, b, c, rep_count)
{
ans <- c - runif(rep_count, a, b)
g <- ans > 0
if (all(!g))
{
return(sum(!g))
}
sum(g) + f_in(a, b, ans[g], sum(g))
}
f_in(a, b, c, rep_count)/rep_count + n + 1
}
sapply(1:5, FUN=function(x){f_new(0, 1, x)})
system.time(f_new(0, 1, 1))
运行结果:
> sapply(1:5, FUN=function(x){f(0, 1, x)})
[1] 2.717814 4.670792 6.666049 8.666784 10.667196
> system.time(f(0, 1, 1))
用户 系统 流逝
1.24 0.02 1.25
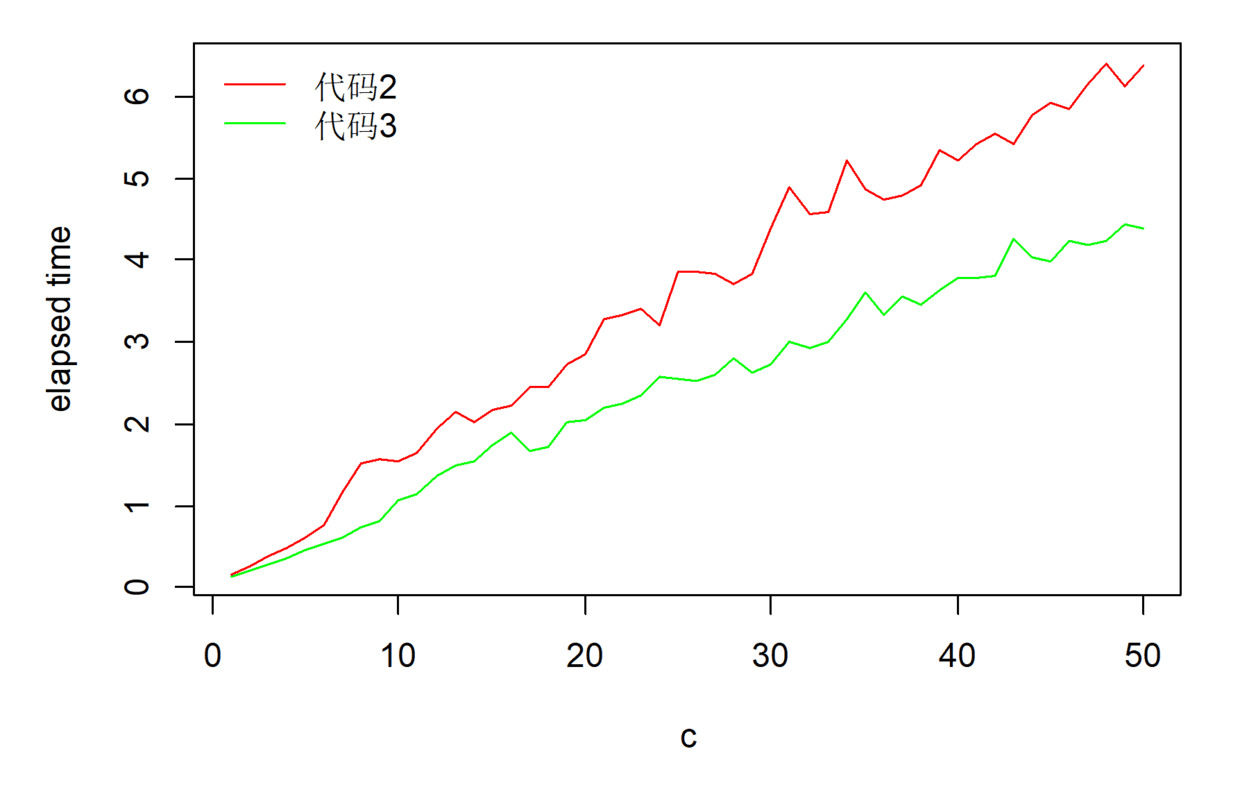
4. 比较 (2)和 (3)
t1 <- sapply(1:50, FUN = function(x){
system.time(mean(f(0, 1, x, rep_count = 1e6)))["elapsed"] })
t2 <- sapply(1:50, FUN = function(x){
system.time(f_new(0, 1, x, rep_count = 1e6))["elapsed"] })
plot(1:50, t1, col = "red", type = "l", xlab = "c", ylab = "elapsed time")
lines(1:50, t2, col = "green", type = "l")
legend("topleft", legend = c("代码2", "代码3"), lty = c(1, 1),
col = c("red", "green"), bty = "n")