LeetCode No.189 旋转数组

原题链接

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

示例 1:

输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]

尽可能不要使用新的空间

环状代替

一次循环，每个数字去找旋转之后的位置，然后从新位置的数字开始继续去旋转之后的位置，直到每个数字都移动过一次。

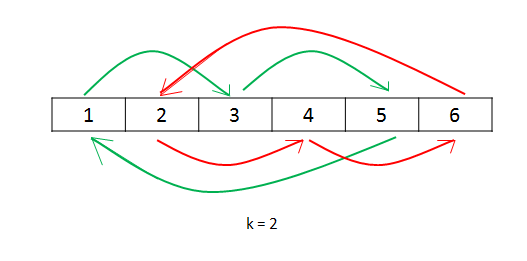
    // 环装替代
    public void rotate(int[] nums, int k) {
        k = k % nums.length;
        int count = 0;
	// 循环，退出条件为count=数组长度
        for (int start = 0; count < nums.length; start++) {
	    // 记录开始位置
            int current = start;
            int prev = nums[start];
	    // 此处while退出条件是防止偶数长度数组的循环。如上图所示
            do {
		// 移动位置，移动次数+1
                int next = (current + k) % nums.length;
                int temp = nums[next];
                nums[next] = prev;
                prev = temp;
                current = next;
                count++;
            } while (start != current);
        }
    }

反转

这个方法基于这个事实：当我们旋转数组 k 次， k%n 个尾部元素会被移动到头部，剩下的元素会被向后移动。在这个方法中，我们首先将所有元素反转。然后反转前 k 个元素，再反转后面 n−k 个元素，就能得到想要的结果。

假设 n=7n=7 且 k=3k=3 。

原始数组 : 1 2 3 4 5 6 7
反转所有数字后 : 7 6 5 4 3 2 1
反转前 k 个数字后 : 5 6 7 4 3 2 1
反转后 n-k 个数字后 : 5 6 7 1 2 3 4 --> 结果

代码实现：

    // 使用反转
    public void rotate2(int[] nums, int k) {
        k = k % nums.length;
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.length - 1);
    }

    // 旋转数组
    private void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start++;
            end--;
        }
    }