第65题——矩阵中的路径

题目：

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。 例如

矩阵中包含一条字符串"bcced"的路径，但是矩阵中不包含"abcb"路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

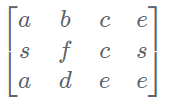
思路： 回溯法

• 创建一个大小为矩阵长度的布尔型数组flag，用来表示矩阵对应位置是否已经走过了，初试全部置为false；
• 创建judge()方法，用来判断走到当前位置是否可以匹配str[]对应位置
• 根据行数和列数，遍历矩阵，找到匹配str第一个字符的i，j下标
• 确定递归终止条件：1越界，2当前字符不匹配，3flag对应位置为true，表示已经走过，这三种情况直接返回false，说明此路不通
• k=str.length-1，说明之前都匹配成功
• 递归判断周围4个位置是否和str[k+1]匹配，只要有一个匹配，就又在其周围4个位置判断和str[k+2]
• 走到这一步，说明匹配不成功，则将flag置为false，进入下一轮匹配

Java

package nowcoder;

public class S65_HasPath {
    public boolean hasPath(char[] matrix, int rows, int cols, char[] str){
        boolean[] flag = new boolean[matrix.length];
        for (int i=0;i<rows;i++){
            for (int j=0;j<cols;j++){
                if (judge(matrix, i, j, rows, cols, str, flag,0))
                    return true;
            }
        }
        return false;
    }
    //judge方法（矩阵，i， j，行数，列数，需匹配的字符串，是否走过标志，判断的第k个）
    private boolean judge(char[] matrix, int i, int j, int rows, int cols, char[] str, boolean[] flag, int k){
        int index = i * cols + j;
        if (i< 0 || j< 0 || i>=rows || j >= cols || matrix[index] != str[k] || flag[index] == true)
            return false;
        //如果k走到str的最后一位，说明匹配成功
        if (k == str.length-1)
            return true;
        //要走的第一个位置flag置为true，表示走过了
        flag[index] = true;
        //回溯，每次找到了就k+1，否则倒回一步
        if (judge(matrix, i-1, j, rows, cols, str, flag, k+1)||
        judge(matrix, i+1, j, rows, cols, str, flag, k+1)||
        judge(matrix, i, j-1, rows, cols, str, flag, k+1)||
        judge(matrix, i, j+1, rows, cols, str, flag, k+1)){
            return true;
        }
        //走到这一步说明周围的没有找到，回退一步,试其他路径
        flag[index] = false;
        return false;
    }
    public static void main(String[] args){
        S65_HasPath s65 = new S65_HasPath();
        char[] matrix = {'a', 'b', 'c', 'e', 's', 'f', 'c', 's', 'a', 'd', 'e', 'e'};
        char[] str = {'b', 'c', 'c', 'e', 'd'};
        char[] strs = {'a', 'b', 'c', 'b'};
        System.out.println(s65.hasPath(matrix,3,4,str));
        System.out.println(s65.hasPath(matrix,3,4,strs));
    }
}