前言

此系列是本人对于学习计算机图形学过程中的记录及总结，所看教材是《Fundamentals of Computer Graphics (FOURTH EDITION)》。本文的图片也主要来源此书。以博客作为学习记录，理解之中若有不足还请大佬们指教。

在变换矩阵章节中，学到了如何使用矩阵在三维空间或二维空间中变换几何对象。本章将讲述变换矩阵的第二个重要作用：将三维空间中物体位置转移至二维平面上的位置。这个三维至二维的匹配转换称为观察变换（viewing transformation）。在object-order rendering中，观察变换非常重要，我们需要很快地找到三维位置在二维平面的映射。

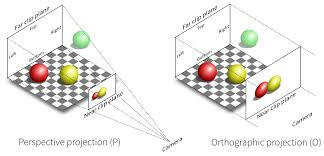
在学习第四章光线追踪时（光线追踪是image-order rendering），介绍了透视视图、正交视图及根据不同视图产生viewing rays。本章的介绍顺序和以上相反（。。说实话我个人不喜欢这种倒序），将会阐述如何使用矩阵变换去表示平行视图和透视视图。

对于视图变换本身来说，其将三维空间的点投射到图像平面的能力仅仅在线框（wireframe）渲染上表现较好。线框渲染仅显示物体对象的线框，同时距离人眼视角较近的表面不会遮盖住较远的表面。如下图：左图为正交视图的线框渲染，中间图为透视视图的线框渲染，右图为遮挡了线条的透视视图。

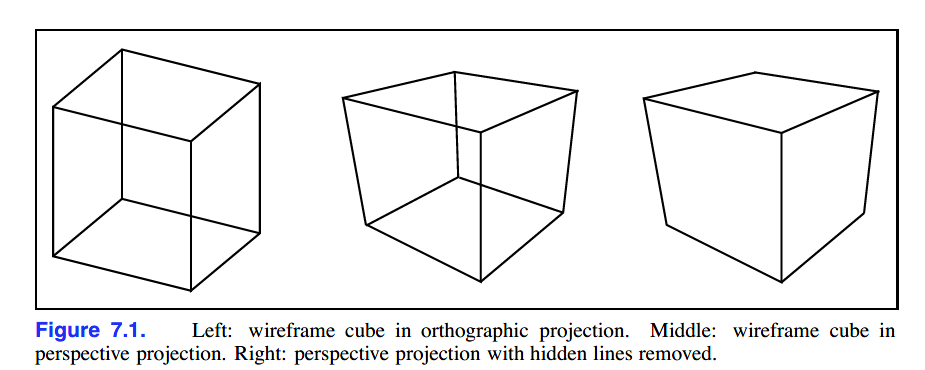
当然，object-order rendering中，也要像ray tracer一样找到距离最近的表面，这会在后面的章节中讲到。本章将讲述仅使用线段绘制三维模型。

书中本章讲述顺序为了更加顺畅，一些需要的点都会暂时忽略（比如z坐标），而会在后续章节在讲述其作用。

7.1观察变换（Viewing Transformations）

观察变换的主要工作是匹配三维位置到二维图像平面像素点位置。这个过程需要考虑许多不同的东西，比如相机位置与朝向、投影类型、视野、图像分辨率等等。因此所有的复杂变换会被拆分为几个稍简单点的变换，多数的图形系统使用以下变换队列：

• camera transformation（相机变换？）或者eye transformation：此变换将相机置于合适朝向的原点。矩阵取决于相机的位置、朝向、pose
• projection transformation（投影变换？）：此变换会投影相机空间（camera space）中的点，使得所有可见点落入x和y，范围在-1至1之间。矩阵取决于投影类型
• viewport transformation（视口变换？）或者windowing transformation：此矩阵maps this unit image rectangle to the desired rectangle in pixel coordinates（。。这里不知道怎么用中文表诉，匹配图像矩阵至所需矩阵的像素坐标系？）。矩阵取决于输出图像的尺寸和位置。

下图展示了各个变化所起的作用：

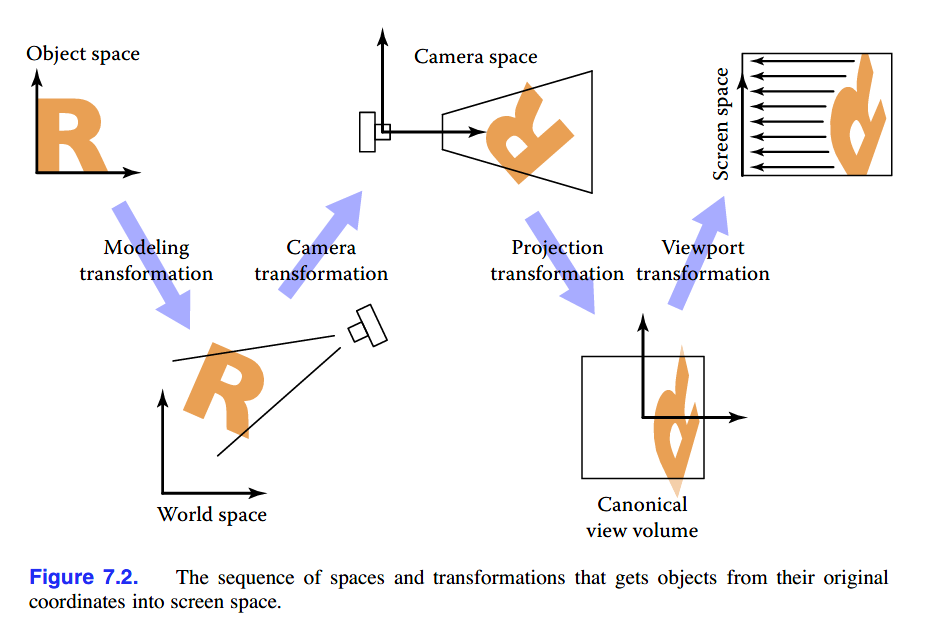
camera transformation将canonical coordinates（或称为world space）中的点转移至相机坐标系（camera coordinates），也可以说是将点置入相机空间（camera space）；projection transformation将相机空间中的点移至规范视域体（canonical view volume,之后用CVV简称）；最后，viewport transformation匹配cvv至屏幕空间（screen space）。

CVV是一个基于笛卡尔坐标系，各点坐标范围在-1至1的方体，如图：

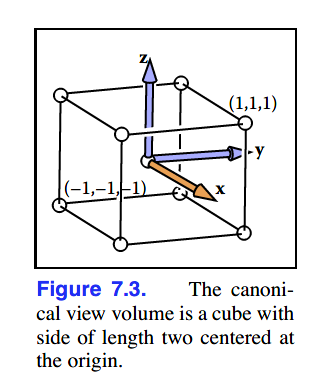
以上每一个变换都是不同的，接下来会以正交视图先作为例子，然后再到透视视图。书中讲述例子时顺序也跟以上队列相反，是从viewport transformation到projection transformation，再到camera transformation。

7.1.1视口变换（The Viewport Transformation）

先讲视口变换，因为视口变换在各种条件下都是通用的。

假设我们想要观察的几何体是在CVV之中，同时使用正交视图，沿着-z方向查看。我们把x=-1投影至屏幕左侧，x=1投影至屏幕右侧，y=1投影至屏幕顶部，y=-1投影至屏幕底部。因此这个方形范围是[-1, 1]*[-1, 1]。

现在回忆下第三章中涉及到的像素坐标系，像素坐标值为整型类型，图像边缘会有半个像素超过边界外。

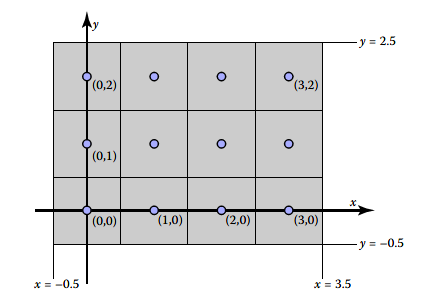
如果我们要把内容绘制到nx * ny大小的图像上，就需要把[-1, 1]*[-1, 1] 映射至[-0.5, nx-0.5]*[-0.5, ny-0.5]。

再次强调现在先假设所有的线段绘制在CVV之中，在后续学习到*裁剪（clipping）*时再不撤销此假设。

因为viewport transformation做的是变换轴对齐矩形（axis-aligned rectangle）至另一个轴对齐矩形，其做的变换就是矩阵变换中windowing transformations的一个具体情况：

windowing transformations：

代入viewport transformation运用就有：

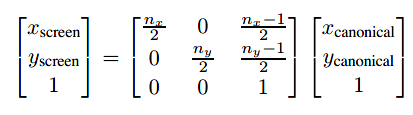
以上还不是完全的viewport matrix，我们可以注意到公式中忽略了z坐标，其仍然能成立是因为由CVV到图像平面，z坐标的值并不会影响点映射到哪个位置。

但是在viewport matrix中会考虑z坐标，但其并不会改变z值。z值的主要作用是隐藏被遮盖的表面，这会在书中第八章提到，第七章暂时不需要它。

viewport matrix如下：

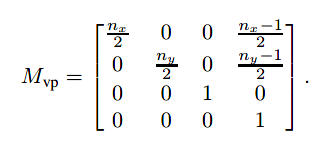
7.1.2正交投影变换（The Orthographic Projection Transformation）

正交投影中，view volume也是一个轴对齐盒子（axis-aligned box），其坐标系为[l, r] * [b, t] * [f, n]，这个view volume被称为orthographic view volume：

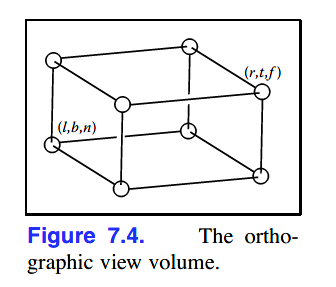
各字母对应解释如下：

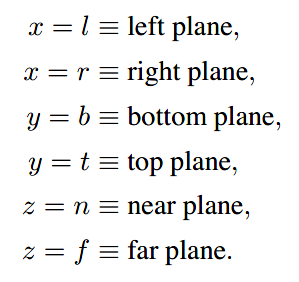
远近的含义如图示：

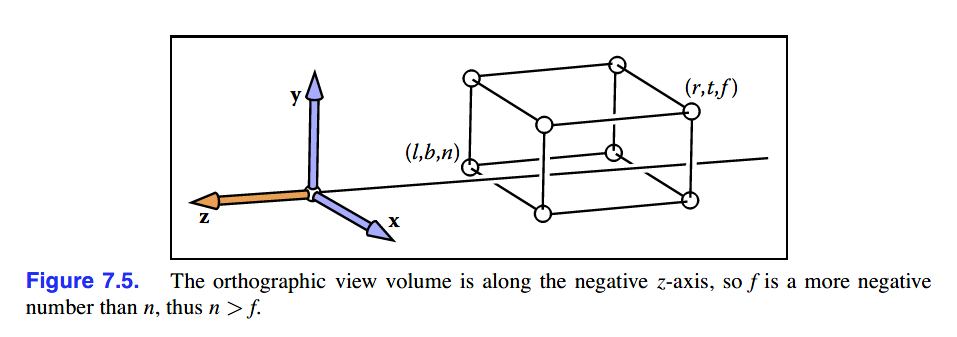
将orthographic view volume转移至canonical view volume的transformation是三维的一种windowing transformation，代入公式后就有了这个转移矩阵：

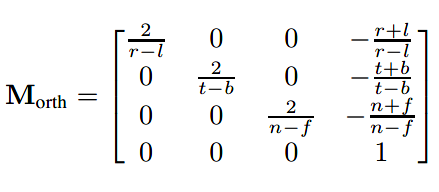
在把三维线段绘制到二维平面上时可以忽略z坐标。结合正交投影变换矩阵与视口变换矩阵，可以对orthographic view volume中的坐标进行如下转换至像素坐标系上（或者说屏幕坐标系。。别名太多了。。）

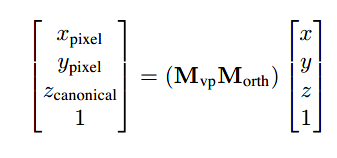
由于z坐标是在CVV中的值，其范围为[1, -1]，现在在暂时不管他，他会在后面章节的z-buffer算法中使用到。

绘制三维线段的算法如下：

ai，bj表示线段的端点。

7.1.3相机变换（The Camera Transformation）

在三维场景中，我们需要改变视点，同时使用任意方向观察场景。有许多的规范可用于表示相机的位置及朝向。本章中我们使用以下规范：

• the eye position e,
• the gaze direction g,
• the view-up vector t.

如图

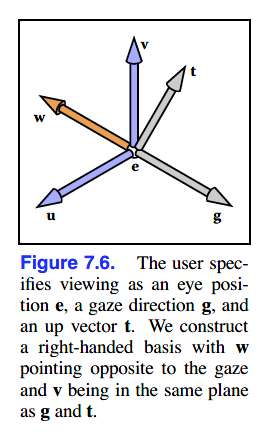
根据g与t，我们可以创建一个原点为e、uvw为基向量的坐标系

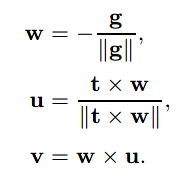
物体对象点的位置是用世界坐标系原点o与xyz为基向量表示的，接下来我们把所有点的位置从xyz坐标系转移至uvw坐标系，就完成了到camera space的转换。在本书第六章中也学习到了坐标系的转换，代入公式即可，因此相机变换的矩阵为：

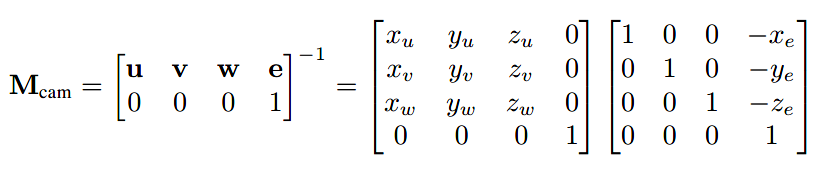
综上内容，整个过程伪代码如下表示：

7.2透视变换（Projective Transformations）

本小节先介绍透视变换作为铺垫，下一小节再讲解透视投影。

透视的关键是屏幕上物体对象的尺寸与1/z是成比例的，用公式与图片说明如下：

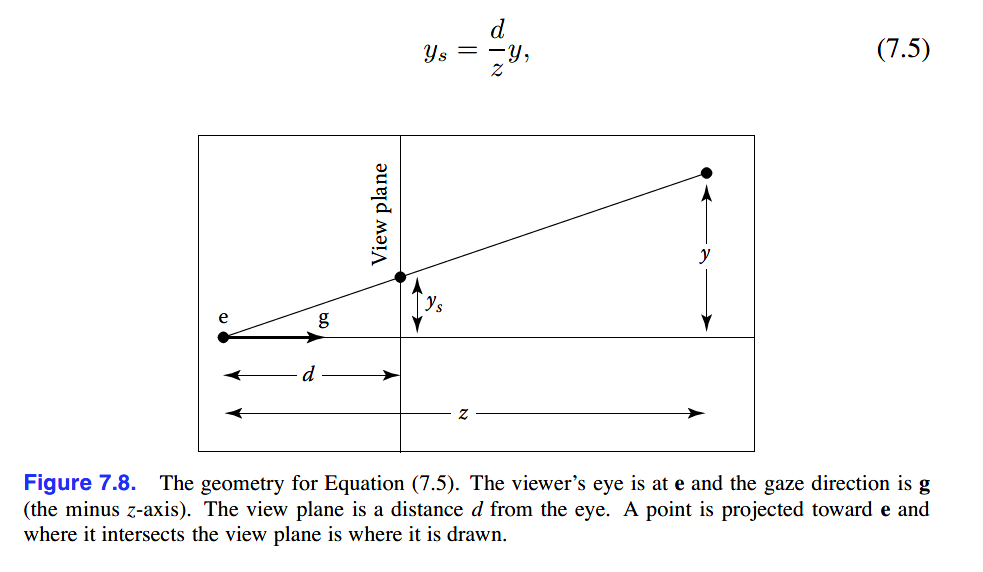
由于上式中存在z作为分母，所以单纯的仿射变换无法做到。

我们可以做一个分离，利用齐次坐标，使用[x y z w]代表(x/w, y/w, z/w)。

回顾之前，线性变换使得可以做如下变换：

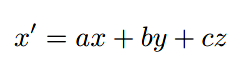
仿射变换进一步扩展：

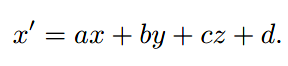
将w作为分母，便有：

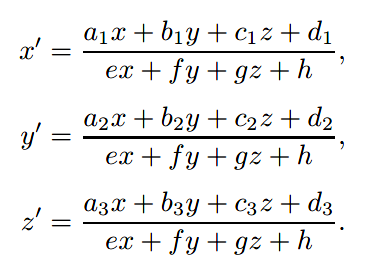
此表达被称为线性有理函数（linear rational function）

用矩阵则表示为：

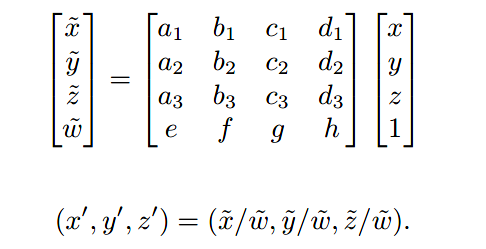
同时，对于此矩阵有如下特性：

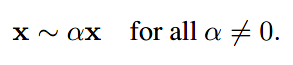
任意系数a（除了0）不会改变矩阵效果。

拿上文中的公式进行举例，应用此变换。

图中仅仅有二维，y与z

根据上文，利用如下变换

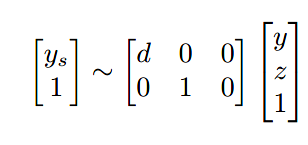
即可将二维的齐次坐标[y;z;1]转换为一维的齐次坐标[dy z]。此一维齐次坐标代表点(dy / z)。

7.3透视投影（Perspective Projection）

在透视投影中，把距离近的平面作为投影的平面，所以相机到图像的平面即为-n。

用n表示距离，上一小节中图像平面映射的公式即为：

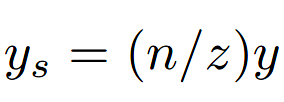
x同理。

根据7.2小节中的线性有理函数，得到透视矩阵（perspective matrix）（注意，还不是透视投影矩阵！！）：

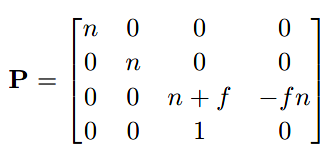
第一、二、四行用于实现上文的透视公式，第三行的目的与正交矩阵和视口矩阵一样，保留z值，后续用于隐藏远处表面。此矩阵无法保持z值不变，但能使得点在近平面和远平面上时，z值不变。

应用P矩阵后的xyz即有如下变换：

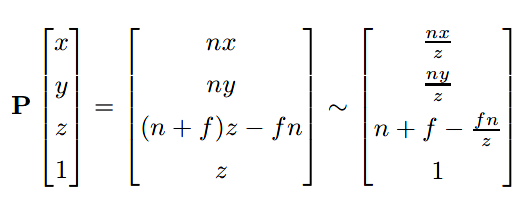
可以看到在近平面(z = n)上和远平面(z = f)上时，z值并不会发生改变。x值与y值也是被z所除。

另外，变换保持了z=n与z=f之间z值的相关顺序，允许了深度排序（depth ordering），这对后续用于隐藏表面非常重要。

有时候也会用到P的逆矩阵，使变换后的z值还原。

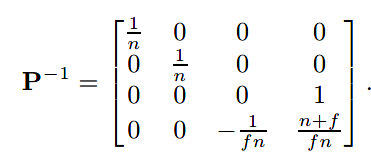
接下来是透视矩阵（perspective matrix）最优雅的地方了，我们可以直接乘上正交变换以获得CVV，因此正交视图的机制也应用其中，而我们仅仅做的只是添加P矩阵及坐标值被w所除。

如下公式，我们即能获得透视投影矩阵（perspective projection matrix）：

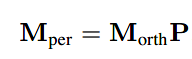
现在还有一个问题是如何决定透视中的l, r, b, t。由于在z=n的平面上，l, r, b, t并未发生改变，可以以在z=n平面上指定l, r, b, t的值。

结合上文的视口变换、相机变换，我们可以得到透视视图的变换矩阵：

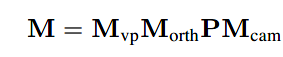
整体算法如下：

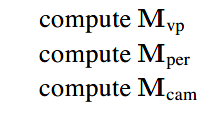
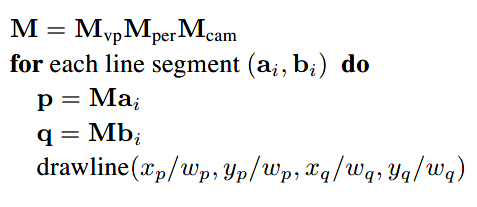
与上文正交视图算法相比，除了矩阵的变换外，仅仅的改变是有被齐次坐标w所除。

最后，看下透视投影矩阵M的样子：

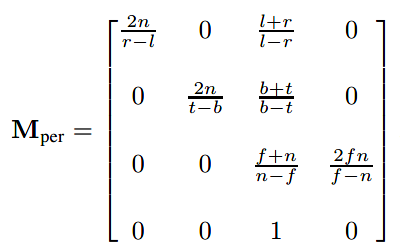
许多文档都会出现相似的矩阵，当我们了解其来源是两个矩阵相乘后，也不会感到多么神秘了。

比如OpenGL：

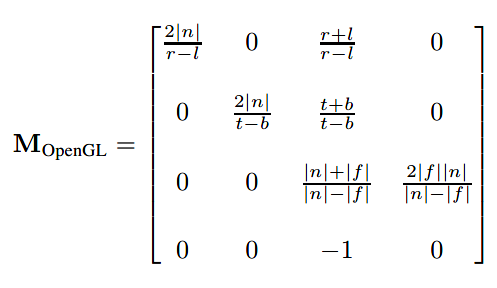
7.4透视变换的一些性质（Some Properties of the Perspective Transform）

透视转换的一个重要性质是转换后线对应线，平面对应平面，view volume中的线段对应view volume中的线段。

本小节主要讲的是一点数学证明，在此不做赘述了

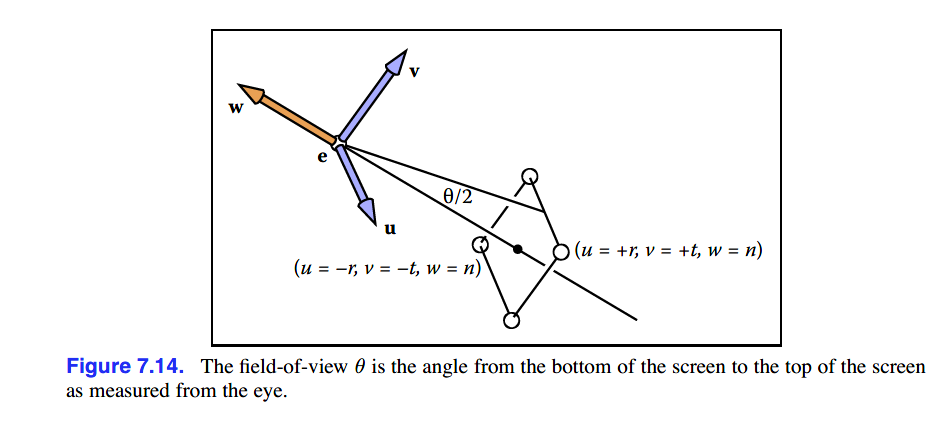
7.5视野（Field of view）

之前一直使用(l, r, b, t)和n来定义窗口，但是我们可以进一步获得一个更加简单的系统，这个系统中相机朝向窗口的中心，这意味着增加了l=-r，b=-t的约束。

进一步增加像素为正方形的约束（没错，确实有不是正方形1：1的像素，详见文末参考资料），便有r与t的比值等于垂直像素数与水平像素数的比值相等：

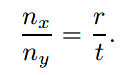
一旦nx与ny被指定了，就仅仅有一个自由度。对应的角度也被称为视野（field of view）

为了区分于水平夹角与对角夹角，此视野也被称为垂直视野（vertical field of view），根据这个特点，我们也可以得到：

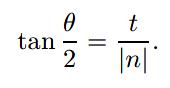
如果知道θ和n值，就可以得到t值，然后使用代码去得到更多的常规viewing system。在一些系统中，n值会因为某些原因是硬编码的，因此会使得有更少的自由度。

总结

本章主要了解了在光栅化过程中，如何使用矩阵变换来表示点在不同坐标系的位置，以此完成三维到二维的变换。

参考资料

正则坐标（Canonical coordinates）- Wikipedia
投影矩阵推导(翻译)
Axis-aligned object - Wikipedia
有理函数（Rational function）- Wikipedia
视野（Field of View）- Wikipedia
为什么有的屏幕象素点不是正方形的？出现不同像素长宽比的原因是什么？ - 知乎
自由度 (统计学) - Wikipedia