深入浅出分布式唯一ID

vevlins
4,132 阅读14分钟

为什么需要分布式唯一ID

传统的单机情况下，通过内存或者数据的主键就可以维护一个唯一ID，但随着业务增长，免不了增加主机和分库分表，在这种情况下如何表示一个唯一的订单或者用户呢？

这就是分布式唯一ID的意义。如果并非此场景，利用数据库自增值或者时间戳随机种子(为避免1ms内碰撞，可以再维护几位顺序位，可以参考后文snowflake算法)即可。当然由于绝大多数分布式唯一ID算法效率很高，想用也是可以的。

分布式唯一ID的要求

分布式唯一ID的要求可以拆解为三个层面：

  1. 不重复。本质上不要求随机，单纯递增也可以，因为不需要避免被猜测。很多时候以随机代替不重复(随机算法够好池子够大，能够极大程度避免碰撞)。
  2. 细化不重复这一要求到时间唯一和空间唯一两项。如果单纯以当前时间戳作为种子，伪随机数生成器在同一时刻、不同机器可以得出相同结果(下文有介绍原因)。
  3. 还有一个隐含的要求是有序，分布式唯一ID需要作为被频繁查询的索引列。数据库索引的基本原理是B+树，通俗来说，是一个子节点更多的二叉搜索树，所以需要有序,最好是纯数字，可以避免字符类型排序的字符集转换消耗。

真随机和伪随机，系统及语言层面方案

从根本上说，计算出来的数字都不是随机数。“真”随机真在这种随机性跟物理世界的随机是一致的，来自于大气运动、分子热运动等我们在物理世界中找不到确切规律预测下一个值的物理运动。至于这些到底是不是随机的，就上升到另一个层面了，从我们的认知来看它们就是真实随机的。“伪”随机伪在下一个值可以计算出来，只是规则比较复杂，在不知道确切的“种子”时无法计算。

既然是计算出来的，就一定有公式，这个公式的要求是什么？

  1. 算出来像随机，结果应该是很均衡的，不存在某些值比率过高。
  2. 不能太复杂，速度要快。
  3. 逆向猜解成本比较高。

目前绝大多数(部分有密码学要求的随机算法可以取系统的熵池)语言的随机算法都是伪随机，比如线性同余、梅森旋转、平方取中，其中最著名的是“线性同余法”（LCG），其公式为

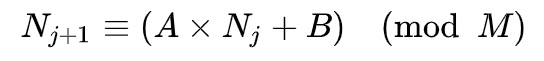
LCG公式
其中Nj就是我们常说的随机数种子，A、B、M则一般由语言实现内定。在种子一定的情况下，输出的“随机”序列也完全一致。最简单的验证方式是golang中的随机算法，如果不指定种子(默认为1)，多次计算得出的序列都一样。

计算得出的序列也是有准确长度的，走完一次会再重新循环。具体长度取决于A、B、M三个值的具体取值，但总小于等于M。

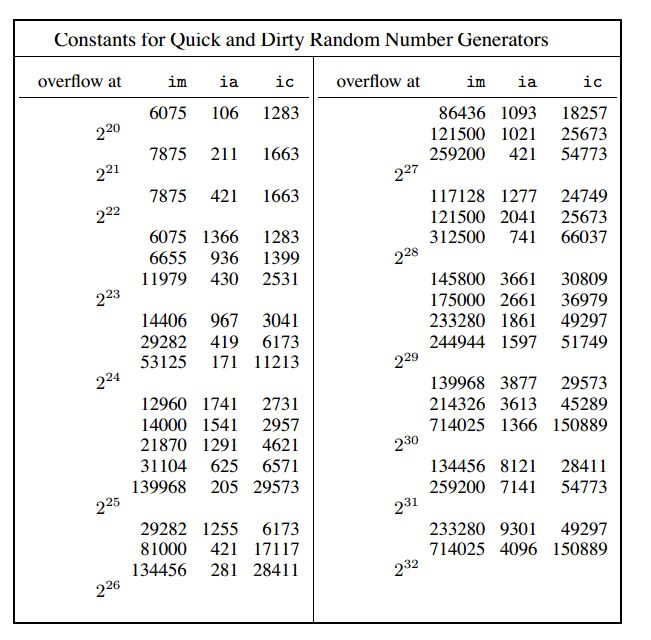
为了随机效果，A、B、M三个值也有一定要求(参考资料中百科链接)。这里是一些被挑选出来，某些编程语言可能内置的值：

LCG常见参数
为了证明这种“伪”随机其实有明显规律，有人利用物理熵(大气)和线性同余算法生成的随机值绘制了两张图片：

利用物理熵：

利用物理熵

线性同余：

线性同余

密码学上把随机数分为三种：

  1. 弱随机数：统计学伪随机性，比特流中01出现频率基本相同，比如这里说到的线性同余。
  2. 强随机数：密码学安全伪随机性:“不能通过给定的随机序列的一部分而以显著大于1/2的概率在多项式时间内演算出比特序列的任何其他部分”，比如Trivium、SHA-2算法，一个随机数算法是否是密码学安全伪随机数生成器有CSPRNG验证集。
  3. 真随机数：具备不可重现性。而由于计算机的计算结果是确定的，所以无法利用算法实现，只有利用熵池实现。

为了获取真随机数，CPU芯片内置了真随机数发生器TRNG和伪随机数发生器PRNG，其中TRNG是利用放大电路的热噪声来产生随机数，而PRNG使用线性反馈移位寄存器，这是一种硬件层面的伪随机数生成器，其种子是TRNG中的真随机数。

（此段待考，可以关注笔者在v2ex的提问/dev/(u)random 是基于 cpu 中的真随机数生成器(TRNG)和伪随机数生成器(PRNG)吗？ - V2EX） 对应地，linux实现了/dev/random和/dev/urandom两个虚拟设备，很多语言中密码学安全的算法都是借助读取这两个设备实现的，比如node中的crypto.randombytes。补充一点，有文章声称这两种设备的随机性是一样的(参考资料中知乎专栏)，但笔者没找到更多详细资料支撑这一说法，倾向于认为这个说法是错的。

方案分类

中心节点分发

所谓中心节点分发就是为了避免在分布式的多台机器上得到同样的值，故而将ID计算集中在一台机器上。这种方案优点很明显：不存在各类基于随机数唯一ID算法的碰撞风险，并且可以排序。

mysql或redis等数据库

常用的方案是利用数据库主键的自增且唯一性，通过1605807来获取主键作为唯一ID。这种方案固然可行，但缺点也很明显：这不是分布式的，中心节点的压力会很大。中心节点故障风险性导致其不具备高可用性。

数据库演进

两种比较典型的演进式思路是：

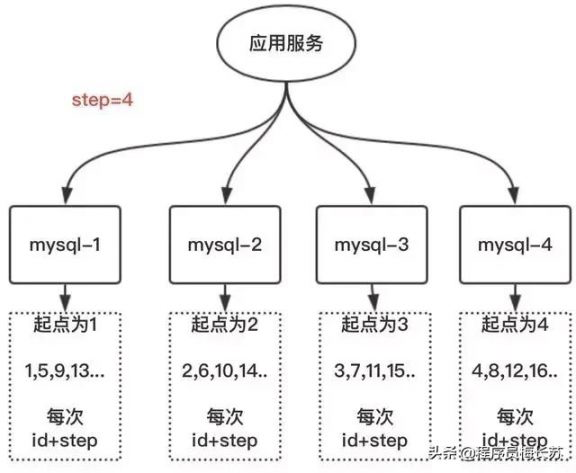
  1. 批量生成一批，均分给每个机器节点，存在它们内存中，枯竭后再生成，实际上这也是所有可能面临效率问题的算法采取的通用方案。
  2. 维护多个中心节点，设置不同起点相同步长，导致它们永远都不重复，比如两台机器一台135，一台246，假如一台宕机，另外一台也可以承担工作，只是效率低点罢了。

mysql实现唯一id

完全随机

还有一些完全依靠随机的算法，这些算法的核心思想就是随机池够大，赌它在可见的产品周期内不足以发生碰撞。其实无论采用什么算法，即使是不使用随机数的中心节点下发方案，也可能因为网络等故障造成重复id，只要业务上设计有一定的保底方案，都不会出问题。比如在数据库将该列设置为唯一索引，插入该订单时会检查订单号是否唯一，如果报错则重试。

Nuid

Nuid是一个较新的算法，其核心非常简单。

使用62个字符(0-9a-zA-Z)生成22位结果，其中前12位是借助TRNG获取的真随机数，而后10位为随机数。

// Generate a new prefix from crypto/rand.
// This call *can* drain entropy and will be called automatically when we exhaust the sequential range.
// Will panic if it gets an error from rand.Int()
func (n *NUID) RandomizePrefix() {
  var cb [preLen]byte
  cbs := cb[:]
  if nb, err := rand.Read(cbs); nb != preLen || err != nil {
    panic(fmt.Sprintf("nuid: failed generating crypto random number: %v\n", err))
  }
  
  for i := 0; i < preLen; i++ {
    n.pre[i] = digits[int(cbs[i])%base]
  }
}

// Generate the next NUID string.
func (n *NUID) Next() string {
  // Increment and capture.
  n.seq += n.inc
  if n.seq >= maxSeq {
    n.RandomizePrefix()
   	n.resetSequential()
  }
  seq := n.seq
  
  // Copy prefix
  var b [totalLen]byte
  bs := b[:preLen]
  copy(bs, n.pre)
  
  // copy in the seq in base36.
  for i, l := len(b), seq; i > preLen; l /= base {
    i -= 1
    b[i] = digits[l%base]
  }
  return string(b[:])
}

其主要优点是性能非常高，1s内可以计算出百万级的id。

uuid部分版本及退化版本

为什么这里叫做部分版本及退化版本呢？

uuid想必大多数人都知道，uuid和guid其实是一回事，只是不同的叫法。uuid是rfc4122标准定义的id算法。其原则上是支持分布式唯一ID的，但具体实现上则不尽然，原因是uuid的标准比较开放，有v1-v5五种版本(v2没有具体实现)，其中有的版本比如v1版本对于node字段的具体取值没有强制约束，最标准的方式是使用当前计算机第一块网卡的mac地址(也有批评暴漏mac地址并不安全，并且mac地址也不能确定唯一不可篡改)，但获取不到的情况下也可以退化成伪随机数。值得一提的是SQL中也有GENERATE_UUID()方法。

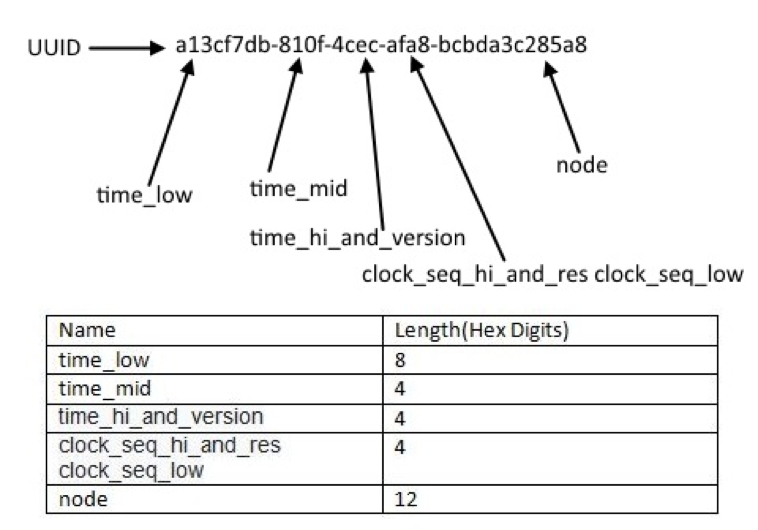
uuid格式

这里不详细介绍所有版本的uuid生成算法，以github上star数量8k+的node uuid npm包的实现为例,其中node节点就没有使用mac地址而是使用随机数(事实上大多数的uuid实现都没有使用mac地址，具体原因待考)：

// rng库的内容是利用crypto.randomBytes从trng熵池读取随机数
var rng = require('./lib/rng');
var bytesToUuid = require('./lib/bytesToUuid');

// **`v1()` - Generate time-based UUID**
//
// Inspired by https://github.com/LiosK/UUID.js
// and http://docs.python.org/library/uuid.html

var _nodeId;
var _clockseq;

// Previous uuid creation time
var _lastMSecs = 0;
var _lastNSecs = 0;

// See https://github.com/broofa/node-uuid for API details
function v1(options, buf, offset) {
  var i = buf && offset || 0;
  var b = buf || [];

  options = options || {};
  var node = options.node || _nodeId;
  var clockseq = options.clockseq !== undefined ? options.clockseq : _clockseq;

  // node and clockseq need to be initialized to random values if they're not
  // specified.  We do this lazily to minimize issues related to insufficient
  // system entropy.  See #189
  if (node == null || clockseq == null) {
    var seedBytes = rng();
    if (node == null) {
      // Per 4.5, create and 48-bit node id, (47 random bits + multicast bit = 1)
      node = _nodeId = [
        seedBytes[0] | 0x01,
        seedBytes[1], seedBytes[2], seedBytes[3], seedBytes[4], seedBytes[5]
      ];
    }
    if (clockseq == null) {
      // Per 4.2.2, randomize (14 bit) clockseq
      clockseq = _clockseq = (seedBytes[6] << 8 | seedBytes[7]) & 0x3fff;
    }
  }

  // UUID timestamps are 100 nano-second units since the Gregorian epoch,
  // (1582-10-15 00:00).  JSNumbers aren't precise enough for this, so
  // time is handled internally as 'msecs' (integer milliseconds) and 'nsecs'
  // (100-nanoseconds offset from msecs) since unix epoch, 1970-01-01 00:00.
  var msecs = options.msecs !== undefined ? options.msecs : new Date().getTime();

  // Per 4.2.1.2, use count of uuid's generated during the current clock
  // cycle to simulate higher resolution clock
  var nsecs = options.nsecs !== undefined ? options.nsecs : _lastNSecs + 1;

  // Time since last uuid creation (in msecs)
  var dt = (msecs - _lastMSecs) + (nsecs - _lastNSecs)/10000;

  // Per 4.2.1.2, Bump clockseq on clock regression
  if (dt < 0 && options.clockseq === undefined) {
    clockseq = clockseq + 1 & 0x3fff;
  }

  // Reset nsecs if clock regresses (new clockseq) or we've moved onto a new
  // time interval
  if ((dt < 0 || msecs > _lastMSecs) && options.nsecs === undefined) {
    nsecs = 0;
  }

  // Per 4.2.1.2 Throw error if too many uuids are requested
  if (nsecs >= 10000) {
    throw new Error('uuid.v1(): Can\'t create more than 10M uuids/sec');
  }

  _lastMSecs = msecs;
  _lastNSecs = nsecs;
  _clockseq = clockseq;

  // Per 4.1.4 - Convert from unix epoch to Gregorian epoch
  msecs += 12219292800000;

  // `time_low`
  var tl = ((msecs & 0xfffffff) * 10000 + nsecs) % 0x100000000;
  b[i++] = tl >>> 24 & 0xff;
  b[i++] = tl >>> 16 & 0xff;
  b[i++] = tl >>> 8 & 0xff;
  b[i++] = tl & 0xff;

  // `time_mid`
  var tmh = (msecs / 0x100000000 * 10000) & 0xfffffff;
  b[i++] = tmh >>> 8 & 0xff;
  b[i++] = tmh & 0xff;

  // `time_high_and_version`
  b[i++] = tmh >>> 24 & 0xf | 0x10; // include version
  b[i++] = tmh >>> 16 & 0xff;

  // `clock_seq_hi_and_reserved` (Per 4.2.2 - include variant)
  b[i++] = clockseq >>> 8 | 0x80;

  // `clock_seq_low`
  b[i++] = clockseq & 0xff;

  // `node`
  for (var n = 0; n < 6; ++n) {
    b[i + n] = node[n];
  }

  return buf ? buf : bytesToUuid(b);
}

module.exports = v1;

uuid的算法与完全随机算法相比加入了时间信息和节点信息，但并不具备很好的排序性。

节点+时序

uuid带节点版本

对应v1版本node字段采用mac地址等硬件地址方案。此处不再赘述。

snowflake雪花算法

Snowflake是twitter提出的一个真正意义上的分布式唯一ID算法，目前业界大厂常用的方案都是snowflake或者基于snowflake的改造和优化。

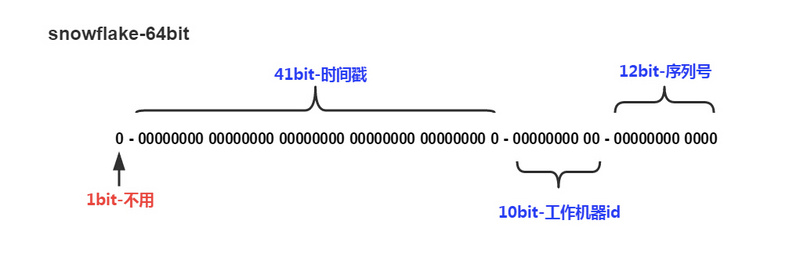
snowflake格式

注意这里的64位是bit位，都是0或者1，而非0-10或者字母。

首位总是0，这是因为snowflake的64位bit实际上是一个64位整型数字，第一位表示数字正负，为0表示正数。41位时间戳支持2^41个数字，以毫秒为单位一共可以表示69年的范围，这里的时间戳并非传统意义的unix时间戳，而是一个自己定义的相对时间，其中的0值可以是业务开始的时刻。10位的工作机器bit可以表示一个分布式系统内最多2^10个机器，这个id也是自己分配的，比如按照ip排序依次为0123。根据上面两个字段，我们已经可以确定在1ms内一个机器上的id不会重复了，为了支持在1ms内更大的并发量，还有12位用来表示在1ms内生成的id的顺序， 单机器单ms内的最大生产效率为2^12个，每秒生产的id也是百万级别。

最终得到的是64位整型数字，满足了分布式ID的各个要求，并且是按照时间顺序有序的。

这里专门提一下机器id，因为这里的id不像uuid使用mac地址，其码段长度与mac地址等硬件地址不容易建立映射关系，一般情况下是通过数据库等中心化的配置中心进行下发。当然如果你的业务并非是自动扩缩容的，那么直接指定也是可以的。从这个意义上讲，snowflake算法并非像某些文章声称的不需要中心节点就可以单机生成唯一id。

snowflake演进

国内的厂商进行的snowflake的改造和优化主要集中在两个方面：

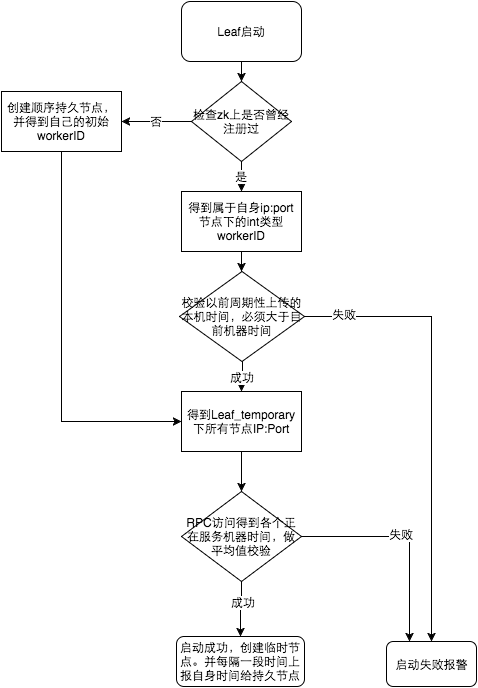
  1. 避免时针回拨。如果41位的时间重复，那么有很大可能出现碰撞的id。美团的leaf方案就是在snowflake外加了一个ZooKeeper来记录时钟前进，如果回拨启动报警。还有很多方案是比较现在生成的id与之前生成的id的时间，如果不是前进则报错或者依旧使用回拨后重复的时间序列+不太可能被用到的较大序列值(赌它不碰撞)。

    leaf时钟回拨策略

  2. 重新划分64位的码段和具体含义，比如当机器较多时可以压缩时钟序列码段，扩大工作机器id码段。

    百度uidgenerator算法

分布式时钟一致

Snowflake是目前最优的分布式唯一ID生成算法，但基于时序的分布式id算法都具有一个显著的问题，没有全局时钟所以不同机器上的时序是有可能不一致的，这并非是分布式唯一ID生成算法的缺陷，而是分布式自己的缺陷，这里提一下可以当作知识拓展。不过这对唯一id本身并无影响，只是时序码段不能作为确切的绝对时间依据。

也有用来维护网络间各个机器的时钟一致性的方案，比如NTP协议或者GPS时钟，但也无法做到完全的同步(几十ms级别的延迟)。至于逻辑时钟，应当与本文探讨的分布式唯一ID关系不大。

结论

在业务量大，要求高的系统中，应当使用改进的snowflake算法。在业务量较小的系统中可以简化使用nuid算法。而在某些非标准的需要前端生成唯一ID的场景下，使用uuid即可(纯前端理论上拿不到真随机数)。

参考资料

avatar
文章
阅读
粉丝