注意点：

二分查找的边界处理需要仔细思考，比如：
- r = len - 1 或 r = len
- l <= r 或 l < r
- m = l + (r - l) / 2 或 m = l + (r - l + 1) / 2
- while 循环里 l = m + 1 或 l = m
- ...
有两种计算中值 $m$ 的方式：
```
  m = (l + r) / 2
  m = l + (r - l) / 2
```
$l + r$ 可能出现加法溢出，也就是说加法的结果大于整型能够表示的范围。但是 $l$ 和 $r$ 都为正数，因此 $r - l$ 不会出现加法溢出问题。所以，最好使用第二种计算法方法。

69. x 的平方根

注：
二分法中 $x=m^2$ 这样判断会超过 int 的界。可以把 temp 设为长整型，或通过 div = x / m 求解。

牛顿法

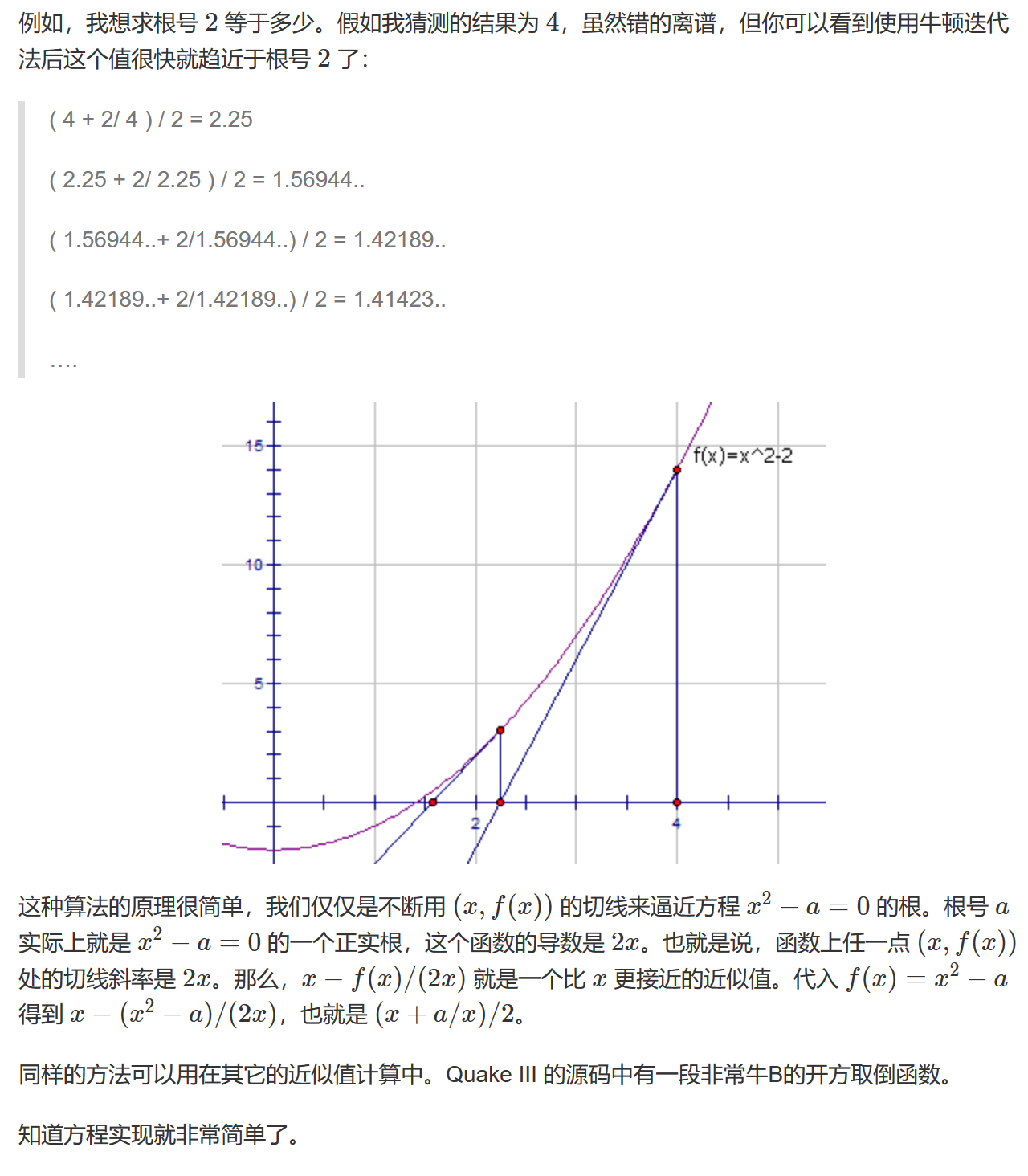
把 $x^2 = a$ 的解看做 $f(x) = x^2 - a$ 与 $x$ 轴的交点，通过不断求 $f(x)$ 上某点的切线与 $x$ 轴的交点来逼近答案。

278. 第一个错误的版本

两个注意点：

如果第 $m$ 个版本出错，则表示第一个错误的版本在 [l, m] 之间，令 r = m；否则第一个错误的版本在 [m + 1, r] 之间，令 l = m + 1。
因为 r 的赋值表达式为 r = m，因此循环条件为 l < r，否则会 l = m = r 引起死循环。

⭐153. 寻找旋转排序数组中的最小值

153 无重复元素

假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )
思路：
判断 $nums[m]$ 和 $nums[0]$ 的大小，若 nums[m] > nums[0] 则说明最小值在右侧，反之在左侧。若数组没有进行旋转，r 会停留在数组末尾，因此最后输出 nums[(r + 1) % len]。
$nums[m]$ 与 $nums[l]$ 或 $nums[r]$ 比较都🉑