💣435. 无重叠区间

贪心思想

从起点的贪心算法

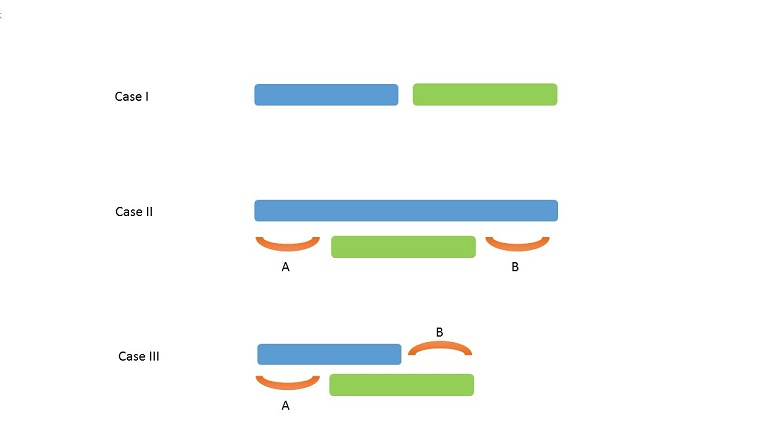
先按照起点对区间进行排序。利用一个 prev 指针追踪刚刚添加到最终列表中的区间。考虑三种情况：

蓝色表示前一个已加入最终列表的区间，绿色为当前区间

• Case 1：
  不移除任何区间，将 prev 赋值为后面的区间，移除区间数量不变。

• Case 2:（一开始只是单纯丢弃了后面的区间）
  只保留后一个区间。因为后一个区间的长度更小，可以留下更多的空间（ 和 ），容纳更多的区间。因此， prev 更新为当前区间，移除区间的数量 +1。

• Case 3:
  这种情况下，我们用贪心策略处理问题，保留前一个区间。（因为前一个区间的右端点更小，可以为后面区间腾出更多空间）prev 不变，移除区间的数量 +1。

从终点的贪心算法

先按照终点对区间进行排序。利用一个 prev 指针追踪刚刚添加到最终列表中的区间。同样地，也考虑上述三种情况：

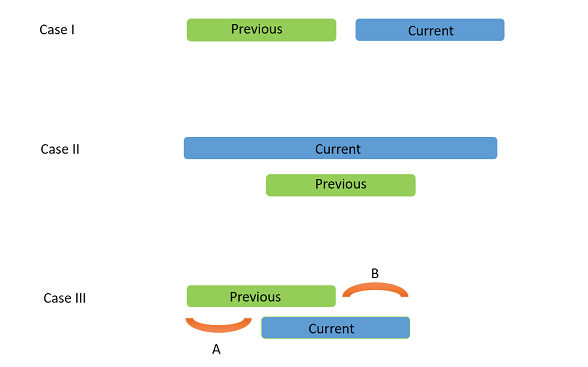
Case 2, Case 3 都是保留前一个区间。

动态规划

见官方题解

452. 用最少数量的箭引爆气球

与上一题思路一样

406. 根据身高重建队列

从逆序生成排列算法

算法如下：

注：

• 二维数组通过 Arrays.deepToString 可直接 sout
• ⭐ toArray() 方法导出的是 Object 类型数组，而 toArray[T[] a] 方法导出的是指定类型的数组，参考这里

121. 买卖股票的最佳时机 I & II & III

I（一次交易）

• 记录今天之前的最小价格，将最小价格作为买入价格，然后将当前的价格作为售出价格，遍历得出最大利润。
• ⭐转化为最大连续子数组（diff数组）求和问题，下方有此题。

参考链接
论坛里也有动规解法

II（多次买卖一支股票）

后一天价格大于前一天则累加。

III（最多两次交易）

正反贪心（很难想到）

• 正向遍历，记录每天卖出时可赚得的最大利润到 forwardMax[]
• 反向遍历，记录 backwardMax，forwardMax[j] + backwardMax 的最大值即为答案。

动态规划解法在“动态规划 markdown”中

605. 种花问题

端点可一起判断
if (flowerbed[i] == 0 && (i == 0 || flowerbed[i - 1] == 0) && (i == flowerbed.length - 1 || flowerbed[i + 1] == 0))

392. 判断子序列

双指针🉑
用 ⭐String.indexOf(Char, fromIndex) 判断更佳。fromIndex 从上一个匹配的位置开始搜索。

⭐665. 非递减数列

在出现 时，需要考虑的是应该修改数组的哪个数，使得本次修改能使 之前的数组成为非递减数组，并且不影响后续的操作。考虑以下测试用例：

用例	0	1	...	i - 1	i	i + 1	...
	...	...	...	-1	(4)	2	...
	...	...	...	3	3	(2)	...
	...	...	...	3	4	2	...
	(4)	2	...	...	...	...	...

可以发现，若 ，则修改 ，否则修改 ，并考虑数组首位情况（用例 4）。

⭐53. 最大子序和

动态规划

状态转移方程：
：表示以 结尾的连续子数组的最大和。 时，直接抛弃之前的和。

分治法（没看懂）