引言:更多相关请看 JAVA数据结构和算法系列
概述
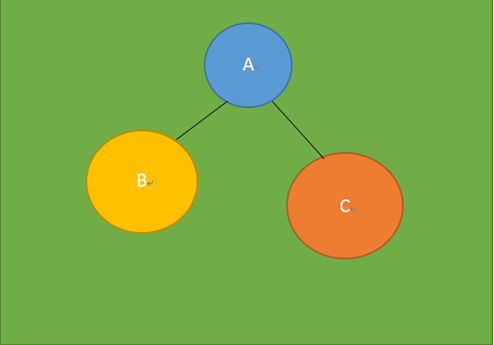
树tree是**有n(n>=0)节点的有限集**。只有零个节点的是空树,大于0的是非空树(有且只有一个根节点root)。除根节点(下图的A节点)外的任意一个节点及其下面所有节点组成的一个集合都可以算是一颗子树(sub tree)。除根节点以外的其它节点(B、C、F等节点)称之为内部节点。
如图:
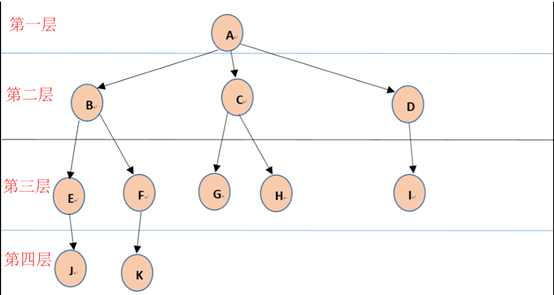
父亲parent、孩子child、兄弟sibling:
父亲:某个节点的直接前面节点。
儿子:某个节点的直接后面节点。
兄弟:同一个父亲的其它节点。
如:A节点的孩子是B、C、D节点,B、C节点的父亲是A节点。B、C节点的兄弟是D节点。
祖先、子孙、堂兄弟:
祖先:就是根节点,如节点A。
子孙:除根节点以外的其它节点都是跟节点的子孙,如节点C、节点E。
堂兄弟:父亲在同一层次的节点互为堂兄弟,如节点J、K;节点F、H。
有序树、M叉树、森林forest。
有序树:一个节点的子节点从左到右依次递增且节点的值大于最左边节点的值。一般没有特别指明,讨论的都是无序树。
M叉树:由一个树中拥有最多度(子节点)的数量决定,是多少度就是多少叉,如上图中的树就是三叉树。(叉的数量大于等于0)。
森林:多颗树(数量大于等于0)的集合。
树的分类
分为B树、B+树、B*树。
B树
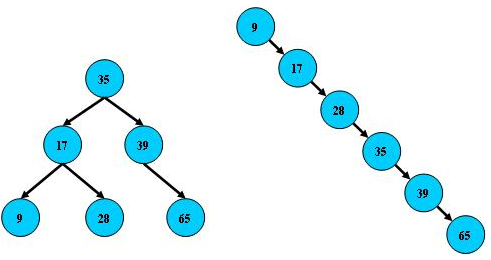
概述:称为B-tree树或B树,也有很多人把B-tree译作B-树,B即Balanced平衡。也可以理解为平衡二叉树的平衡多叉树(叉大于2)。二叉树有个缺点,当经过多次插入与删除后,有可能会导致不同的结构,比如出现下图的右边结构:
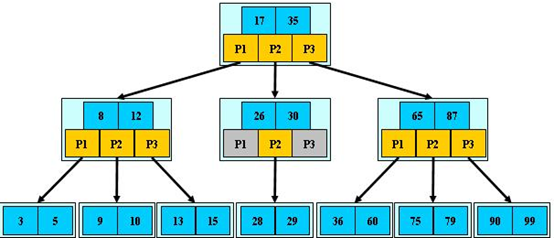
技术案例:硬盘的存储结构(数据类似文件,引用类似文件夹)。
B+树
概述:与B-树(每一层都有数据)相比,是把所有数据都放在最底层,其它层全部都是引用。查询的时候是和和引用的值比较,而不是直接就和数据比较。如图:
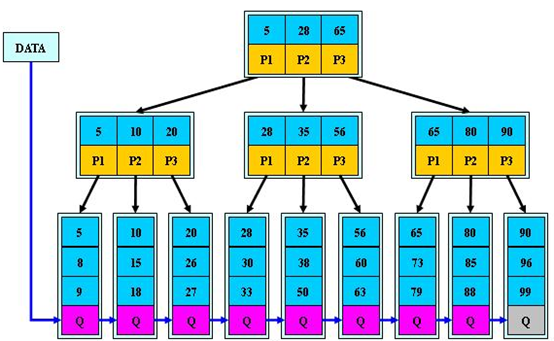
技术案例:数据库的存储结构。
B*树
概述:B+树的变体,在B+树的非根和非叶子结点增加指向兄弟的指针、索引。
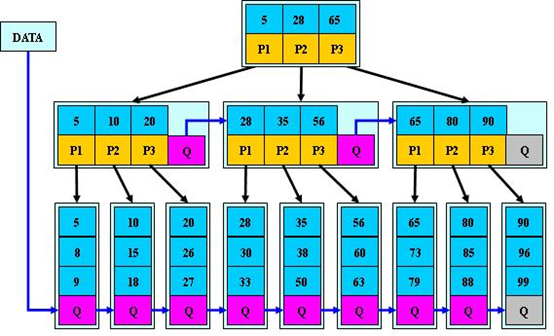
二叉树
概述:binarytree,任意节点的子节点数量(度)都不超过2的树。一般由一个节点A,两颗子树(左子树B,右子树C)组成。左右子树严格区分不能颠倒。
注意:哪怕是只有0个或者1个节点也可称为二叉树。
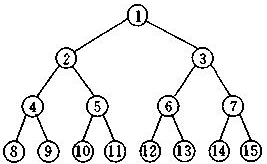
满二叉树:就是指每一层都达到最满层数的树。如1层1个、2层3个(1+2)、三层7个(1+2+4)、4层15个(1+2+4+8)…由此类推。
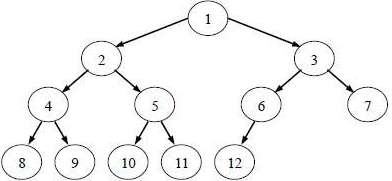
完全二叉树:最下层最右侧去掉相邻的若干节点(大于等于0)的树。
排序二叉树
特性:
左子树上所有节点的值小于它根节点的值。
右子树上所有节点的值均大于它根节点的值。
对排序二叉树进行中序遍历(左根右)将得到一个有序集合。 如图:
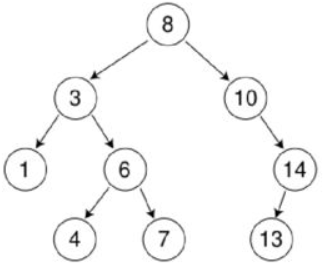
平衡二叉树
在排序二叉树的基础上,增加关于左右两边子树的层级规定。就是从根节点开始,左右两边子树的层级差别只能为正负一。比如我有儿子,你最多就只能有孙子,不能有重孙,玄孙;我还没有儿子,你就最多只能有儿子,不能有孙子。
目的:减少二叉树查找层次,提高查找速度。
常用实现方法:红黑树、AVL、替罪羊树、伸展树、Treap。
红黑二叉树
概述:Red-Black Tree是自平衡的二叉树。节点只有红黑两种颜色。
实现:TreeSet、TreeMap。
特点:根节点只能是红色。第一层级是红色、第二层级就是黑色、第三层级是红色,第四层级是红色……,依次类推。如果一个节点是红色,子节点就只能是黑色。叶子节点(指为null的叶子节点)只能是黑色。
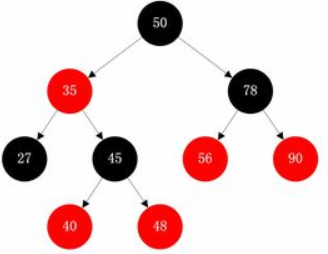
存储结构
概述:分为顺序和链式存储(开发常用)。
顺序存储:把节点数据放在数组中,根据二叉树特性,第i个节点放在第i个位置,i节点的两个子节点数据分别放在下标2i和2i+1里面。当树不是完全二叉树时(也就是左右),会造成空间浪费。
数组存储方式:

二叉树遍历
概述:Traverse,按照某种次序把树中的每一个节点都访问且只访问一次。也可以理解成人为的将非线性结构线性化。树分为三部分:根、左右节点,遍历一般分为三种遍历方式(还有一种按照层次遍历,很少使用)。
先序/根遍历DLR:根、左节点、右节点。
中序/根遍历LDR:左节点、根、右节点。
后序/根遍历LRD:左节点、右节点、根。
注意:根据递归的特性,上面三种模式就是一个递归的概述过程。
下图:
练习:已知一颗二叉树中序遍历4513267,后序遍历5437621,求先序遍历。 答:根据题意得知根1、左子树45、右子树2367。根据中序45和后续遍历54得出先序遍历:145(根加左子树)。右子树的下面通过3267和3762又可分为根2、左子树为3、右子树(根为6、右节点7)。所以先序遍历就是:1452367。可以通过中序遍历和先序后序任意遍历推出剩下的遍历和实例图,但是通过先序遍历和后序遍历无法推出中序遍历。 画图实例:
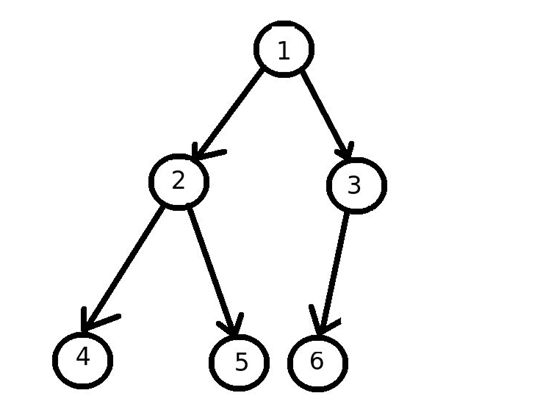
节点类
/**
* @Author:root
* @Description: 节点类 提供节点的相关属性
*/
@NoArgsConstructor
@AllArgsConstructor
public class Node {
// 左子节点引用
Node left;
// 节点数据
Object data;
// 右子节点引用
Node right;
public Node(Object data) {
this.data = data;
}
// 重写toString()
@Override
public String toString() {
return "Node[left:" + left + "\tdata:" + data + "\tright:" + right + "]";
}
}
二叉树类
/**
* @Author:root
* @Description: 自定义二叉树
*/
@NoArgsConstructor
public class BinaryTree {
// 根节点
Node root;
// 节点数量
int size;
public BinaryTree(Node root) {
this.root = root;
}
// 获取节点数量
public void size() {
System.out.println("节点数量为:" + size(root));
}
// 重载方法
private int size(Node node) {
if (node != null) {
// 节点数量等于左右子树节点的数量加一
// 递归调用
return size(node.left) + size(node.right) + 1;
}
return 0;
}
// 判断非空
public boolean isEmpty() {
// 臃肿写法
/*if(root == null){
return true;
}
return false;*/
// 简洁写法 推荐
return root == null;
}
// 获取节点值
public Node getKey(int data) {
return getKey(data, root);
}
// 查询某个节点在某节点范围内是否存在
public Node getKey(Object data, Node node) {
if (node == null) {// 递归结束条件1:如果节点为null直接返回
return null;
} else if (node != null && node.data == data) {// 递归条件结束2:如果找到节点值就返回
return node;
} else {// 递归体
Node a = getKey(data, node.left);// 左子树
Node b = getKey(data, node.right);// 右子树
if (a != null && a.data == data) {// 是否在左子树找到
return a;
} else if (b != null && b.data == data) {// 是否在右子树找到
return b;
} else {// 都没找到,直接返回
return null;
}
}
}
// 获取树的层级
public void hight() {
System.out.println("获取树的层级(level):" + hight(root));
}
// 重载方法
private int hight(Node node) {
if (node != null) {
// 树的层级等于左子树或右子树层级中最大的层次加1.
int nl = hight(node.left);
int nr = hight(node.right);
return nl > nr ? nl + 1 : nr + 1;
}
return 0;
}
// 先序遍历
public void pre() {
// 第一种
/*// 判断根节点不为空
if(root != null){
// 先输出根的值。
System.out.print(root.data);
// 递归循环左子树
BinaryTree leftTree = new BinaryTree(root.left);
// 递归调用
leftTree.pre();
// 递归循环右子树
BinaryTree rightTree = new BinaryTree(root.right);
rightTree.pre();
}*/
// 第二种
System.out.print("先序遍历结果:");
pre(root);// 调用重写方法
System.out.println();// 换行
}
// 重载私有调用
private void pre(Node node) {
// 判断节点不为空
if (node != null) {
// 先输出节点值
System.out.print(node.data + "\t");
// 判断左子树 循环调用
pre(node.left);
// 判断右子树 循环调用
pre(node.right);
}
}
// 中序遍历
public void mid() {
System.out.print("中序遍历结果:");
mid(root);//调用重载方法
System.out.println();// 打印
}
// 私有重载方法
private void mid(Node node) {
// 判断节点
if (node != null) {
// 先循环递归判断左子树
mid(node.left);
// 打印节点值
System.out.print(node.data + "\t");
// 先循环递归判断右子树
mid(node.right);
}
}
// 中序遍历 依靠栈
public void midStack() {
System.out.print("中序遍历 依靠栈结果:");
// 使用双端队列实现栈
Deque<Node> de = new LinkedList<>();
// 引用节点
Node node = root;
// 循环判断
while (node != null || !de.isEmpty()) {
// 第一个:循环
while (node != null) {
// 入栈
de.push(node);
// 先左边
node = node.left;
}
// 第二个:判断
if (!de.isEmpty()) {
// 把出栈的节点赋值给节点
node = de.pop();//把元素移出栈并返回移出元素
System.out.print(node.data + "\t");// 打印节点数据
// 最后是左节点
node = node.right;
}
}
System.out.println();// 换行
}
// 后序遍历
public void post() {
System.out.print("后序遍历结果:");
post(root);// 调用重载方法
System.out.println();//换行
}
// 层次遍历 用栈实现
public void level() {
System.out.println();// 换行
// 必须有个判断,如果节点为空,马上结束, 提高效率
/*if(root == null){
return;//return的两个条件:1是结束循环, 2是返回值
}*/
System.out.print("层次遍历 用栈实现结果:");
// 队列 先进后出 泛型加Node
Queue<Node> queue = new LinkedList<>();
// 增加节点(节点的根) 入队
// queue.add(root);
queue.offer(root);// offer和add方法都可以使用,推荐offer
// 如果长度不为0,就代表节点有值
while (queue.size() != 0) {
// 循环长度, 也就是在某个层次到底有几个节点(长度就是几)
for (int i = 0; i < queue.size(); i++) {
// 临时节点
Node tem = queue.poll();// 出队
System.out.print(tem.data + "\t");// 获取节点值
// 如果左右节点不为空 就把节点加入到队列中 入队
if (tem.left != null) {
// queue.add(tem.left);
queue.offer(tem.left);
}
if (tem.right != null) {
// queue.add(tem.right);
queue.offer(tem.right);
}
}
}
}
// 私有重载方法
private void post(Node node) {
// 判断节点是否为空
if (node != null) {
// 先循环递归判断左子树
post(node.left);
// 再循环判断右子树
post(node.right);
// 打印节点结果
System.out.print(node.data + "\t");
}
}
}
测试类
/**
* @Author:root
* @Description: 测试树
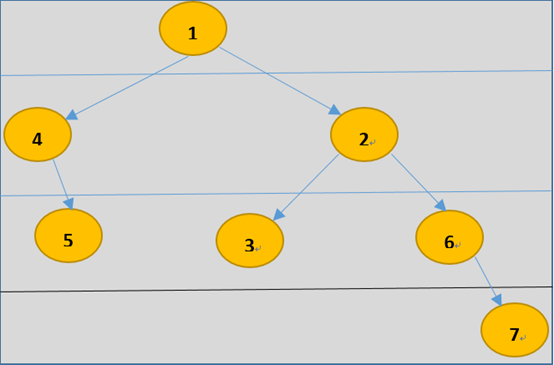
* 先序遍历:124536。中序遍历425163。后序遍历452631。
* 层次遍历:(由上往下、由左往右)1/23/456
*/
public class TestTree {
public static void main(String[] args) {
// 添加节点 一定要从最底层开始,最好是先把图画出来
// 假设再加个第四层
// Node n7 = new Node(null, 7, null);
// 第三层
// Node n4 = new Node(null, 4, n7);
Node n4 = new Node(null, 4, null);
Node n5 = new Node(null, 5, null);
Node n6 = new Node(null, 6, null);
// 第二层
Node n2 = new Node(n4, 2, n5);
Node n3 = new Node(n6, 3, null);
// 第一层 也就是根节点
Node n1 = new Node(n2, 1, n3);
// 添加到二叉树
BinaryTree bt = new BinaryTree(n1);
System.out.println("查看节点:" + n1);
System.out.println("输出节点的值:" + n1.data);
System.out.println("判断是否为空:" + bt.isEmpty());
System.out.println("输出节点值和左右子节点的值:" + bt.getKey(3));
System.out.println("查询某个节点在某节点范围内是否存在:" + bt.getKey(3, n3));
// 获取树的所有节点
bt.size();
// 获取树的层级(level):
bt.hight();
// 先序遍历:124536
bt.pre();
// 中序遍历425163
bt.mid();
// 中序遍历 依靠栈
bt.midStack();
// 后序遍历452631
bt.post();
// 层次遍历
bt.level();
}
}
结果
查看节点:Node[left:Node[left:Node[left:null data:4 right:null] data:2 right:Node[left:null data:5 right:null]] data:1 right:Node[left:Node[left:null data:6 right:null] data:3 right:null]]
输出节点的值:1
判断是否为空:false
输出节点值和左右子节点的值:Node[left:Node[left:null data:6 right:null] data:3 right:null]
查询某个节点在某节点范围内是否存在:Node[left:Node[left:null data:6 right:null] data:3 right:null]
节点数量为:6
获取树的层级(level):3
先序遍历结果:1 2 4 5 3 6
中序遍历结果:4 2 5 1 6 3
中序遍历 依靠栈结果:4 2 5 1 6 3
后序遍历结果:4 5 2 6 3 1
层次遍历 用栈实现结果:1 2 3 4 5 6