本文始发于个人公众号:TechFlow
导数是微积分也是高数当中很重要的一个部分,不过很遗憾的是,和导数相关的部分很多同学都是高中的时候学的。经过了这么多年,可能都差不多还给老师了。所以今天的文章就一起来温习一下导数的相关知识,捡一捡之前忘记的内容。
函数切线
关于导数,最经典的解释可能就是切线模型了。以前高中的时候,经常对二次函数求切线,后来学了微积分之后明白了,所谓的求切线其实就是求导。
比如当下, 我们有一个光滑的函数曲线,我们想要求出这个曲线在某个点
的切线,那么应该怎么操作呢?
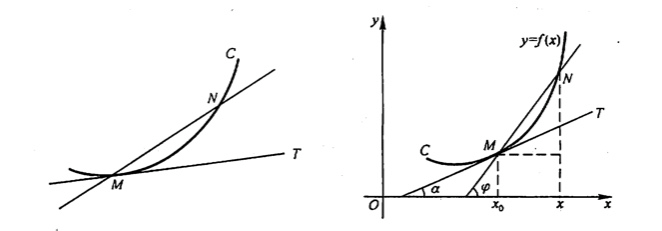
如上图所示,我们可以在选择另外一个点N,然后做MN的割线。假设T是M的真实的切线,当我们将N向M无限逼近的时候,在无限缩小,直到趋近与0,而此时的割线MN也就无限逼近于M点真实的切线T。
在图中,MN的斜率表示为,其中
.
当N逼近于M时:
我们令,所以:
此时的结果就是函数在
处导数的值,上面这个方法大家应该也都不陌生,在物理课上就经常见到,只不过在物理当中不叫极限也不叫逼近,称为换元法。但不管叫什么,意思是一样的。我们理解了上面这些式子之后,再来看看导数真正的定义。
定义
假设函数在点
处的邻域内有定义,当自变量
在
处取得增量
(
仍然在
的邻域内),相应的函数取得增量
。如果
在
时的极限存在,称为函数
在点
处可导。它的导数写成
也可以记成
,或者
。
如果函数在开区间
内可导,说明对于任意
,都存在一个确定的导数值。所以我们就得到了一个新的函数,这个函数称为是原函数
的导函数,记作
。
不可导的情况
介绍完了常见函数的导函数之后,我们来看下导数不存在的情况。
导数的本质是极限,根据极限的定义,如果。那么,对于某个正数
,对于任何正数
,都有
时,
。那么就称为
时,
的极限是a。
我们对上面的式子进行变形,可以得到,当时:
也就是说极限存在的条件是无论自变量从左边逼近还是右边逼近,它们的极限都存在并且相等。所以,函数
在
点可导的充分必要条件就是,函数在
处的左右两侧的导数都必须存在,并且相等。
另一种不可导的情况是不连续,不连续的函数一定不可导。这一点其实很难证明,我们可以来证明它的逆否命题:可导的函数一定连续。
根据导数的定义,一个点的导数存在的定义就是在
时存在。即:
我们把极限符号去掉:
这里的a是时的无穷小,我们队上式两边同时乘上
,可以得到:
由于都是无穷小,并且
存在,所以
也是无穷小。而连续的定义就是当
时,
也趋向于0.
反例
我们来举一个反例:
它的函数图像长这样:
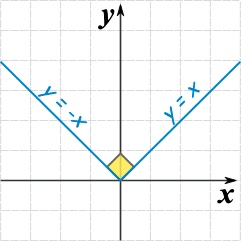
我们试着来证明:在
处不可导。
由于在
处的左右导数不等,和极限存在的性质矛盾,所以
在
处不可导。
常见函数的导数
我们再来看一下常见函数的导函数,其实我们了解了导数的定义之后,我们完全可以根据导函数的定义自己推算。但说实话,这些推算意思不大,所以我们直接跳过推算的部分,直接来看结论。
,C是常数。
,
,
,
,
,
,
当然我们实际运用当中遇到的当然不只是简单的函数,很多函数往往非常复杂。那么对于这些复杂的函数,我们又应该怎么来计算它们的导数呢?敬请期待我们下一篇的内容。
今天的文章就到这里,如果觉得有所收获,请顺手点个关注吧,你们的支持是我最大的动力。
