这章更完会跳很大一段!yep!直接跳到Lecture 8!因为项目是NLP方向的,现在在看时间更短且针对性更强的CS224n,前面的可能会等到四月份项目结题再看,CS224n里面讲得不清楚的地方我发现Andrew讲得蛮细致,所以直接跳到Sequence Models这一章,开始同时看两个,同时会写CS224n的笔记,反正也没人看我写的这些东西,自由的感觉真好(不想再努力了呜呜呜)
浅层神经网络基础
神经元的计算
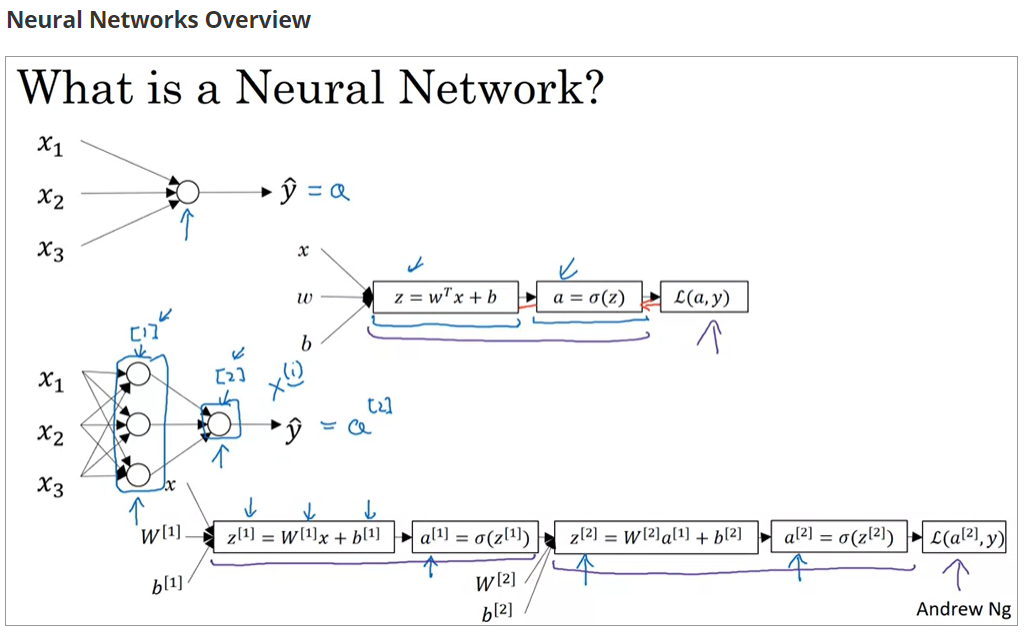
- 计算
,这里的
包含了转置的操作,当
时,
,即为输入
- 计算
,其中
是神经网络当前层的激活函数,而后将结果输出到下一层
神经网络的输入输出
若记和
分别为输入和输出结果,那么它们的结构如下:
- X -- input dataset of shape (input size, number of examples)
- Y -- labels of shape (output size, number of examples)
这里要注意所代表的输入大小即为输入层神经元个数(样本向量长度)
神经网络的表示
神经网络一般可以看作的结构,分为:
- 输入层(Input layer):大小为每个样本具有的向量长度
- 隐藏层(Hidden layer):数量与连接方式自定义
- 输出层(Output layer):大小为计算的结果具有的向量长度
层数不包括输入层,因此最简单的神经网络是两层的神经网络
符号表示
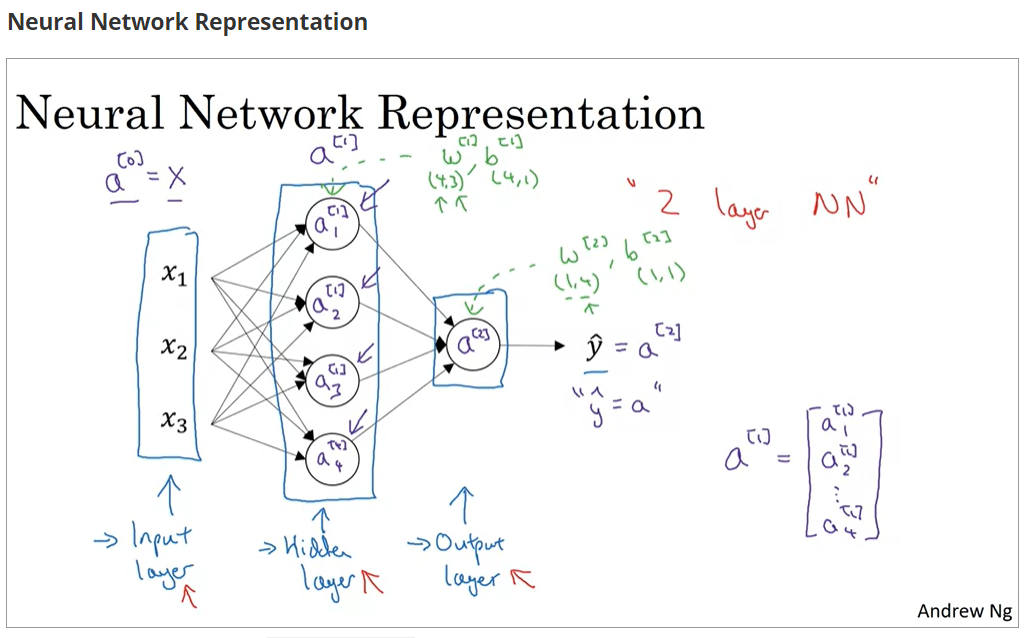
假设,可以看到
的值每一层都不同,其矩阵大小分别由输入和输出决定
-
设
w.shape == (m,n),那么m == 该层的神经元数,n == 上一层的神经元数- 直觉上这里应该是反的,但
计算时候加了转置
- 直觉上这里应该是反的,但
-
设
b.shape == (x,y),那么x == 该层的神经元数,y == 下一层的神经元数
上下标符号说明:
:用于上标,表示第几层的变量
:用于上标,表示第几个样本对应的变量,一般只用于
:单独的数字用于下标,表示该变量在本层内隶属于第几个神经元
因此就表示 处于第一层的第四个神经元输出的关于第三个训练样本的激活向量(activation vector)
浅层神经网络的计算
向量化
直接按列堆叠向量,就可以得到正确的表达式,其实正确性就是来源于线性代数的那一套
自己关于向量化的理解:向量化去for loop的本质只是将for循环转换成了矩阵的计算而已
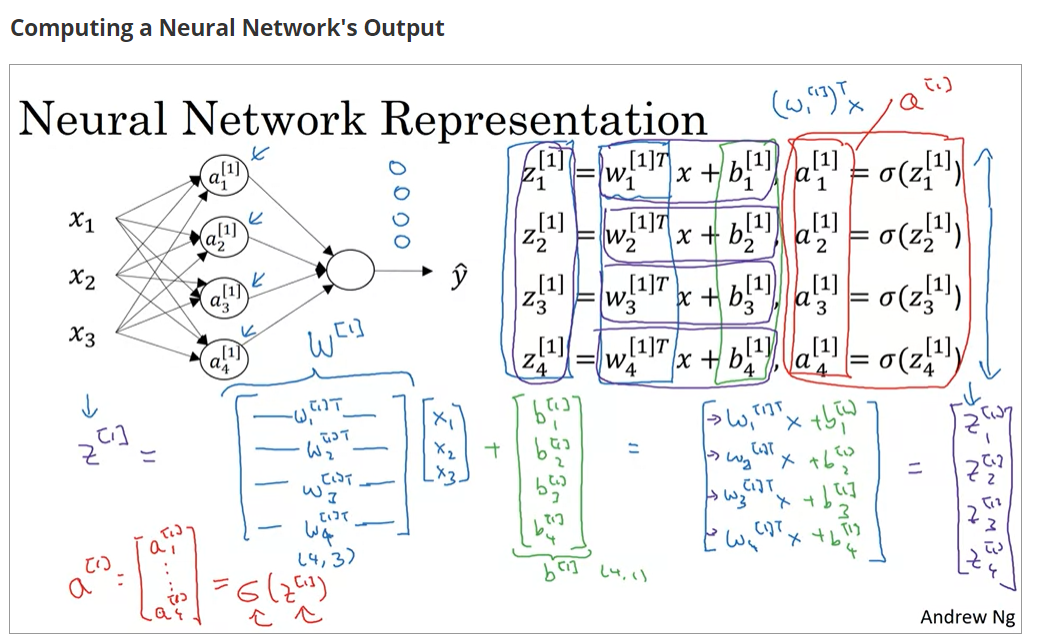
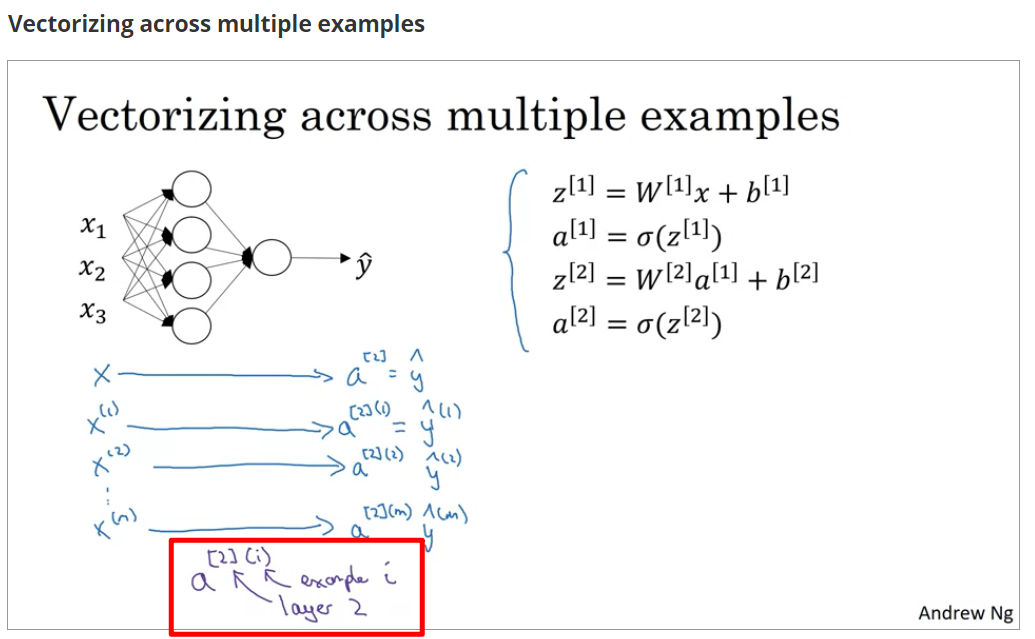
这张图Andrew画得很清楚,看到这里豁然开朗orz
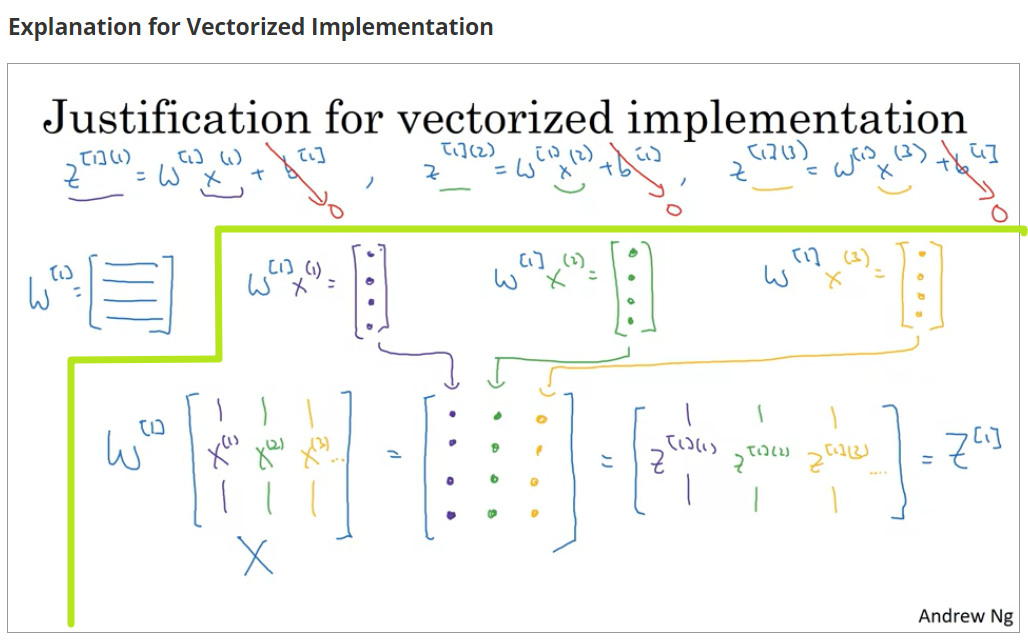
反向传播

随机初始化
在之前的逻辑回归中,将所有和
的值初始化为0是可行的,但在神经网络中,将所有值初始化为0就会出现**对称化(symmetry)**的情况,其实不仅是0,将同一层的
和
以相同常数初始化都会出现这种问题,所以
和
的初始值应保持不同,因此采用随机的方法初始化
关于对称化的含义及来源,可以参考【知识】神经网络中的参数初始化 - 大胖子球花 - 博客园,我个人的理解是梯度下降寻找的是和
的最优解,如果用相同参数初始化,权值也相同的情况下,就会出现一个隐藏层中的神经元无论怎么训练结果都相同的情况,这就造成了神经元的浪费,也不利于整体的训练
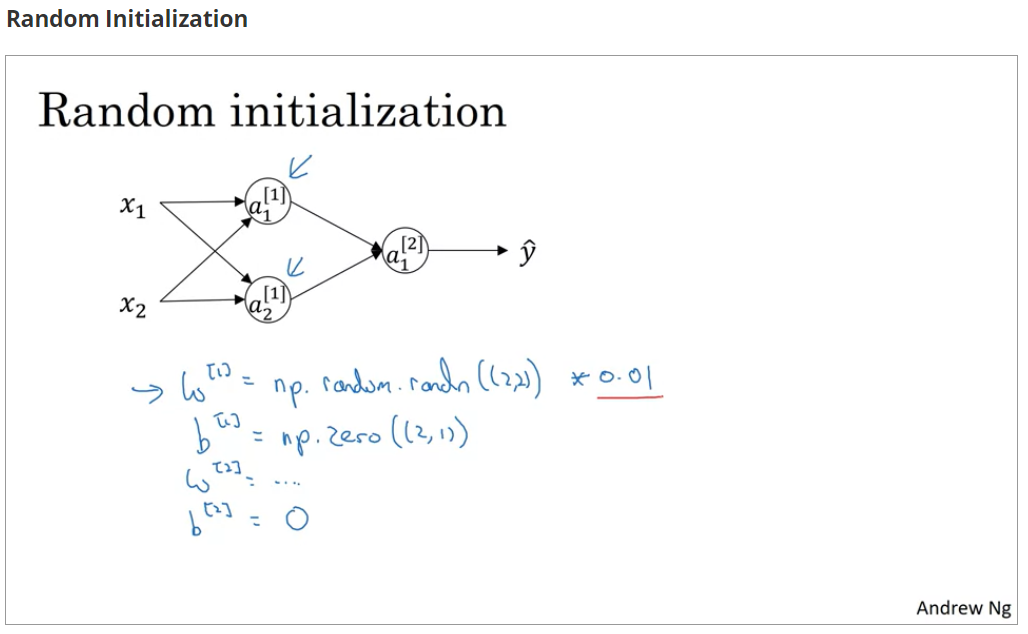
如下图所见,可以将一个神经元用0初始化,其他的全都随机初始化,且乘的系数应该很小,避免过大梯度过小的问题
激活函数
常用激活函数

选取
- sigmoid:二元分类问题
- tanh:浅层神经网络,其实除了二元分类,其他的时候都比sigmoid优秀
- ReLU:常用于深层网络激活函数,有效解决当
的值太大时候梯度下降过慢的问题
- Leaky ReLU:为解决ReLU函数左侧梯度为0的问题,用途不广
下面来自于 www.cnblogs.com/hutao722/p/…
相较而言,在隐藏层,tanh函数要优于sigmoid函数,可以认为是sigmoid的平移版本,优势在于其取值范围介于-1 ~ 1之间,数据的平均值为0,而不像sigmoid为0.5,有类似数据中心化的效果
但在输出层,sigmoid也许会优于tanh函数,原因在于你希望输出结果的概率落在0 ~ 1 之间,比如二元分类,sigmoid可作为输出层的激活函数
但实际应用中,特别是深层网络在训练时,tanh和sigmoid会在端值趋于饱和,造成训练速度减慢,故深层网络的激活函数默认大多采用relu函数,浅层网络可以采用sigmoid和tanh函数
激活函数的作用
这一段老师没讲,大概的思路是这样的:
对于有些样本,用一条直线就可以将它们分开,但是对于大多数样本一条直线并不能满足需求,激活函数的作用就是将线性分割转换成非线性的分割,更细致的可以参照 www.zhihu.com/question/22…
常见激活函数的求导
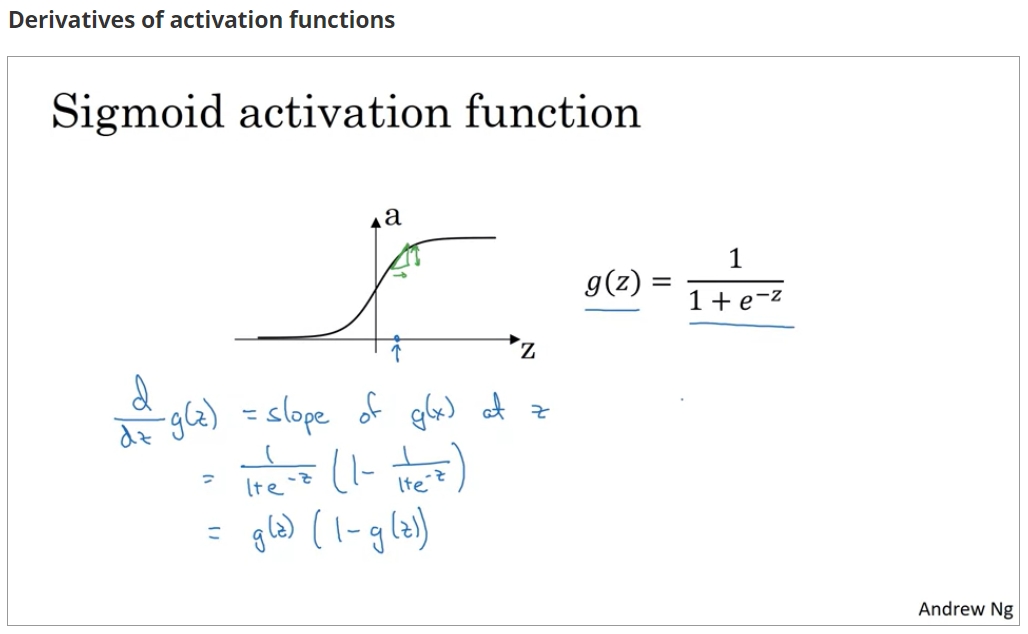
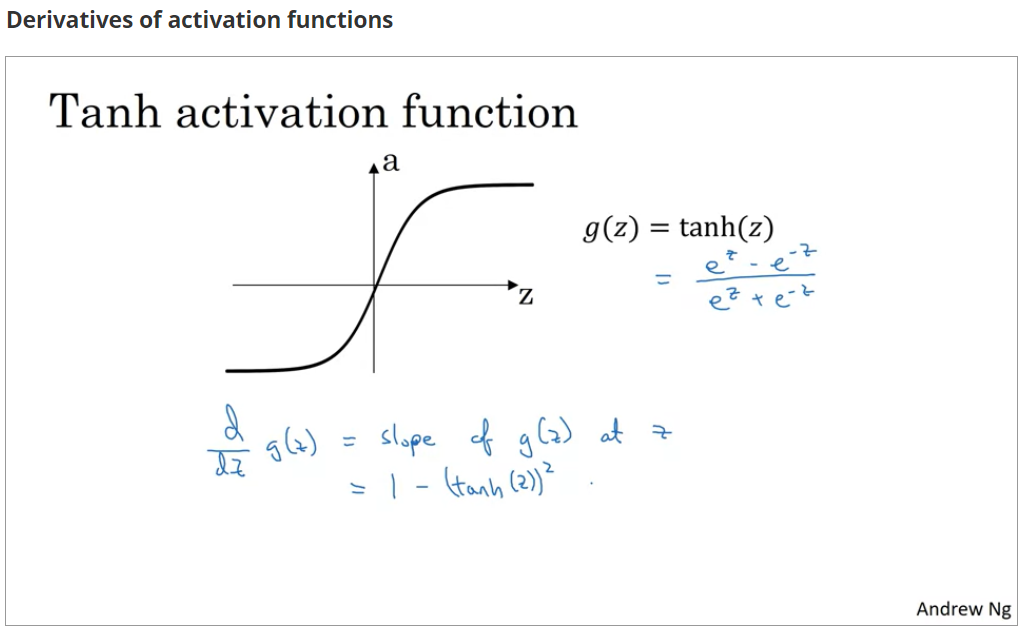

注意点
这里有两道错题
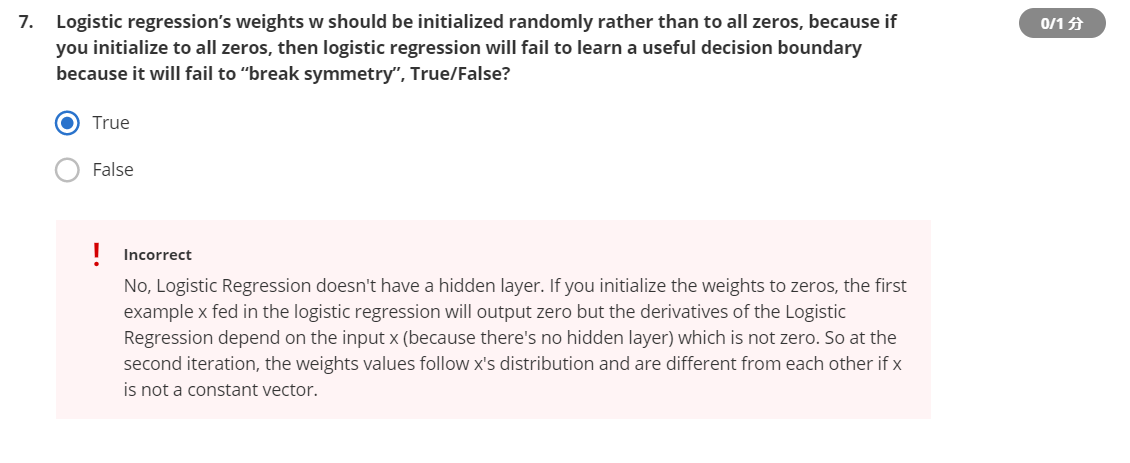
逻辑斯蒂回归的全0初始化
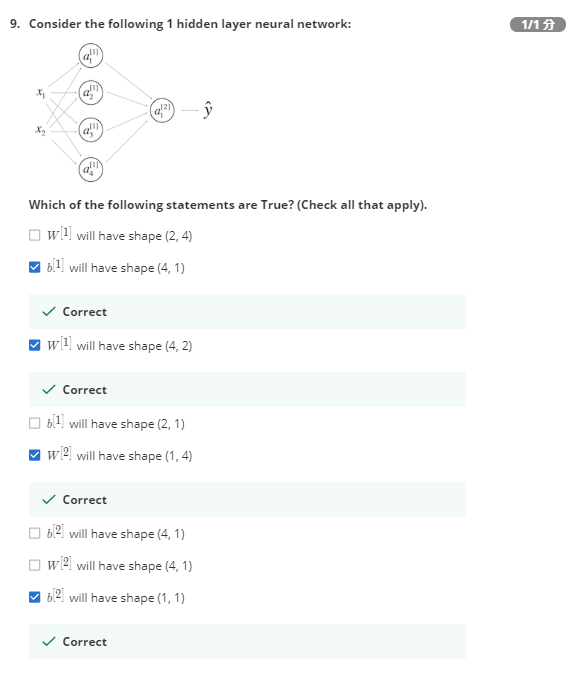
结果输出维度
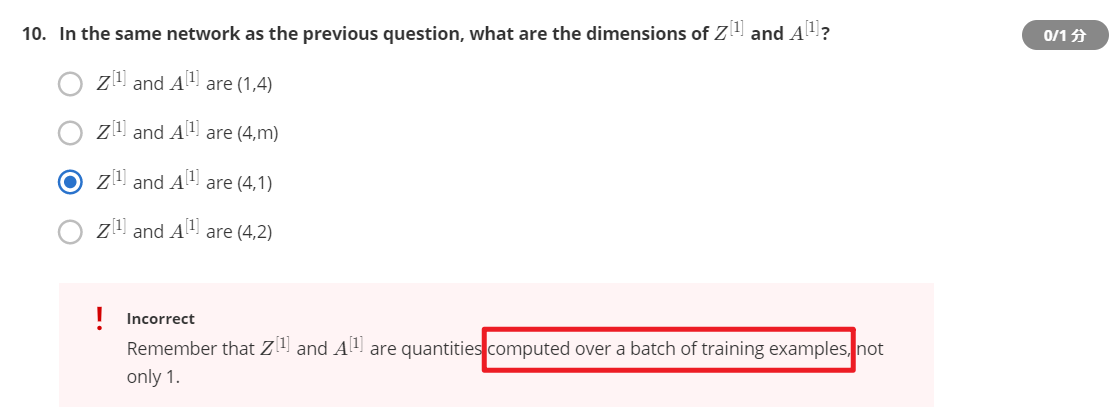
由,这里本来想的是
和
的输出维度与该层的
保持一致,但是其实在计算过程中
从列向量被横向广播到了
个,即样本的个数,因此这道题答案应该是B