背景
在日常生活中,我们可能在地图上划一片区域来进行个性化运营。
比如我在高德地图搜索<北京SKP>,系统会告诉我<北京SKP>商圈范围,并且给我推荐附近的停车场,以及入口大门位置等信息(如下图)。
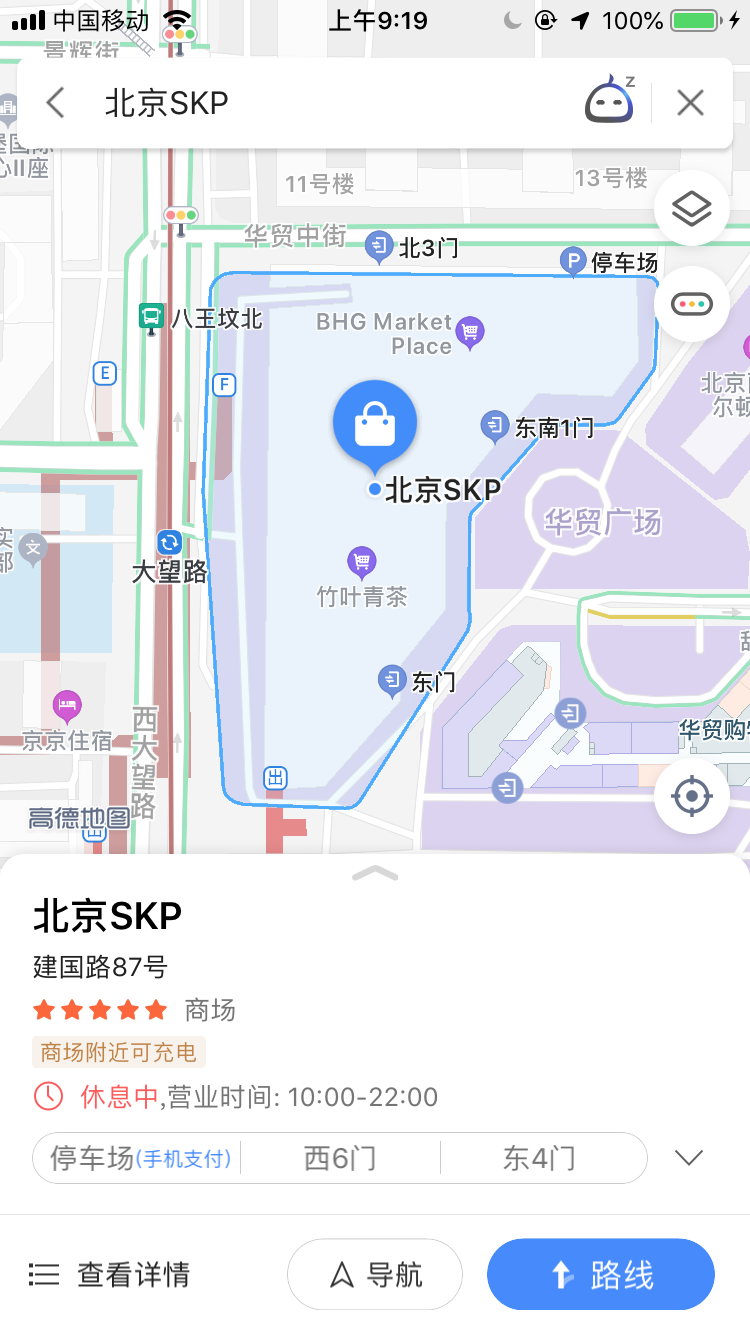
或者在我们日常定外卖的时候。 系统可能根据交通条件、商场分布情况、住宅区等分布情况综合考虑,将城市划分为一个个商圈(如下图)
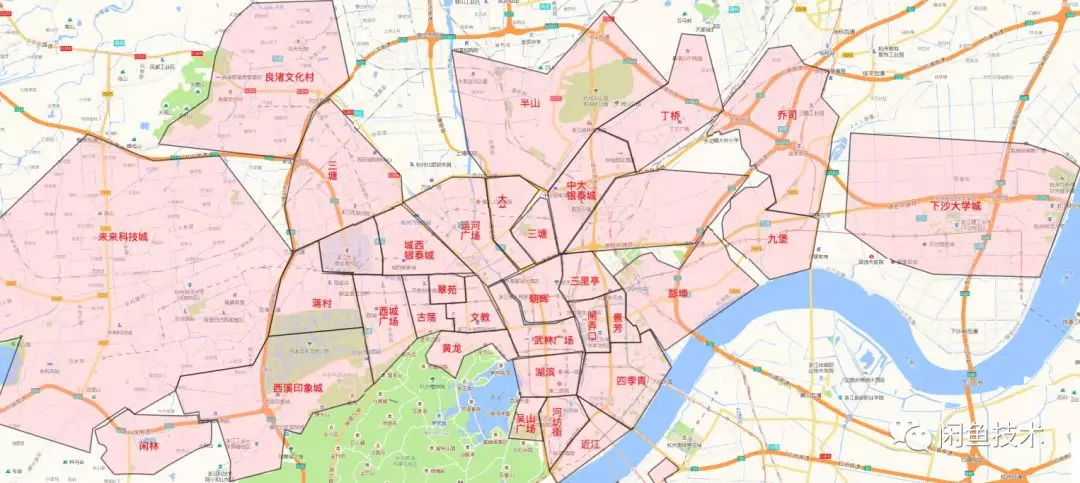
- 图片来自闲鱼技术
实际上用户发布的GPS随机分布在地图上的点数据。当用户处于某个商圈范围内时,APP会向用户推荐GPS位于此商圈中的菜品。要实现各种个性化服务,就需要计算出哪些商品是归属于你所处的商圈。
你可能会有疑问? 这是如何实现的呢? 如何高效判断用户在某个商圈里呢? 此次我们来进行探讨~
名词解释
地理围栏
地理围栏(Geo-fencing)是LBS的一种新应用,就是用一个虚拟的栅栏围出一个虚拟地理边界(实际上围栏是有序的点的集合)
阶段0x01 - 只使用几何相关算法判定
刚才在名词解释的时候已经提到了,地理围栏是有序的点的集合,那我们不妨把用户所处的商圈判定,抽象成用户所处的经纬度是否在有序的点的集合内(既:多边形)
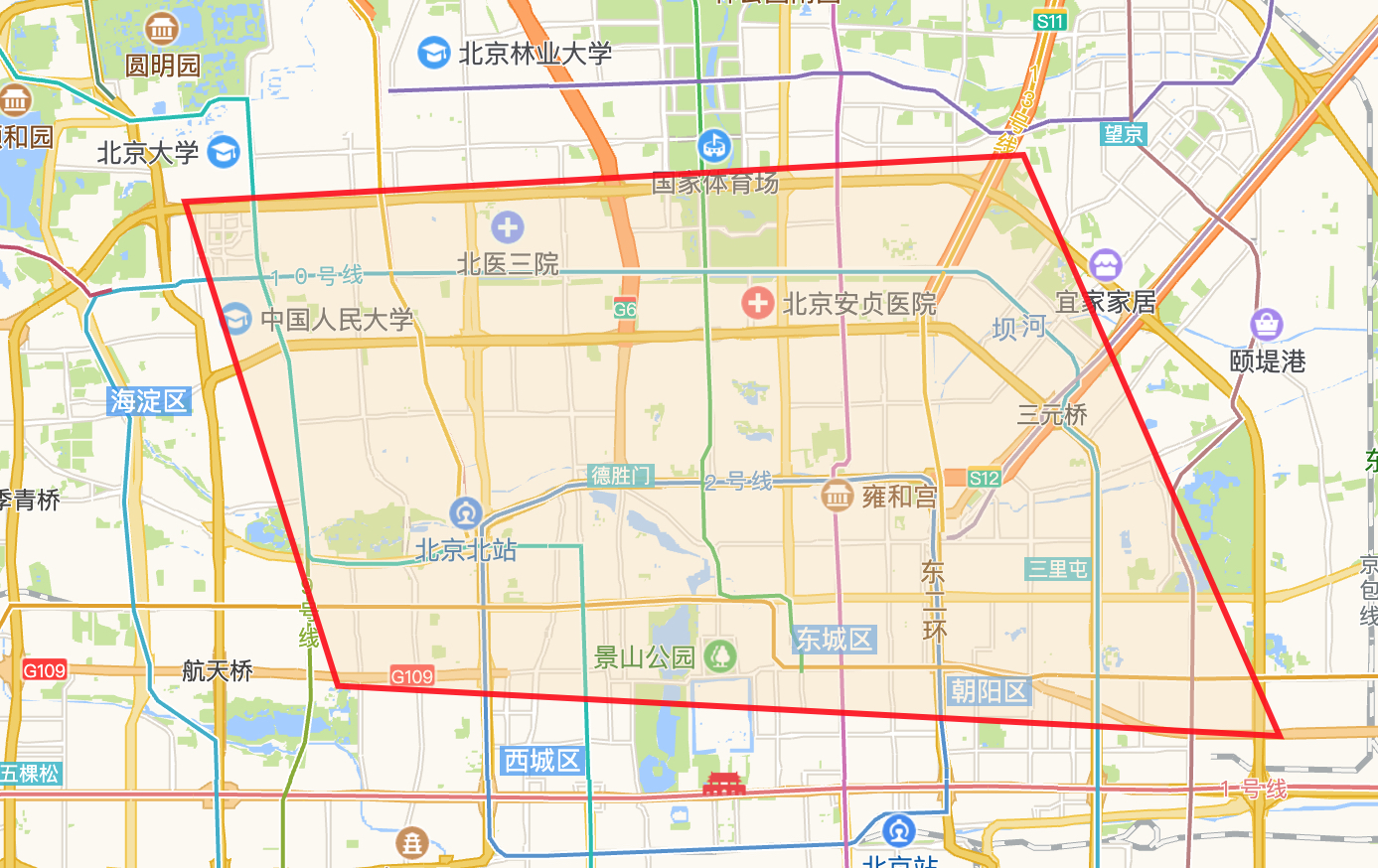
如何判定点是否在多边形内?
在几何学中PIP(Point In Polygon)采用射线法(Ray Casting Algorithm)是一种判断点是否在对边形内部的一种简单方法。
即从该点做一条射线,计算它跟多边形边界交点个数,如果交点为奇数,那么点在多边形内部,否则点在多边形外部
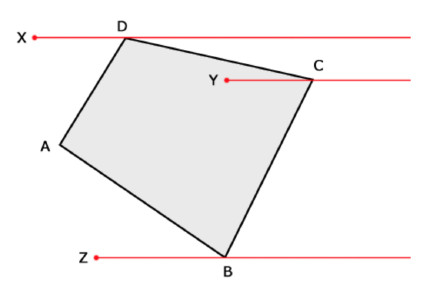
需要注意以下几种特殊情况:
- 点在多边形的顶点或边上
- 点在多边形边的延长线上
- 点的射线与多边形相交于多边形的顶点上
golang相关代码可以参考:geo-ispointinpolygon
优缺点
- 优点:适用于凸多边形和凹多边形
- 缺点:当商圈非常多的时候,只使用射线法是非常低效的
阶段0X02 - 结合空间索引&几何相关算法
上面已经介绍了,当商圈非常多的时候,使用射线法是非常耗时的。
采用空间索引进行快速匹配
常用的空间索引
geohashgoogle-s2uber-h3
geohash原理
简单的来说是将地球理解为一个二维平面,将平面递归分解成更小的子块,每个子块在一定经纬度范围内拥有相同的编码,这种方式简单粗暴,可以满足对小规模的数据进行经纬度的检索
具体可参见:geohash
geohash范围介绍
geohash根据字符串的长度代表着生成矩形覆盖的范围,比如当wx4g29代表着宽为1.2km,高为609m的一个矩形,具体的一些范围如下图:
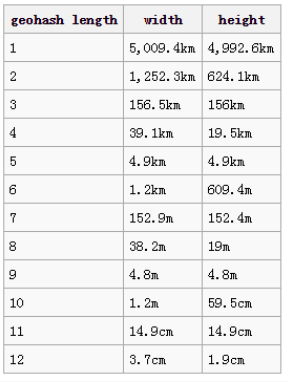
注:需要针对多边形的范围选取不同长度的geohash值
具体步骤
首先我们选取多边形中心点,作为geohash的起始点,既多边形经纬度的和/多边形边数
多边形中心点计算算法
func calCenterAvg(scope [][]float64) []float64 {
sumLng := float64(0) // 经度的和
sumLat := float64(0) // 纬度的和
for _, v := range scope {
sumLng += v[0]
sumLat += v[1]
}
return []float64{(sumLng) / float64(len(scope)), (sumLat) / float64(len(scope))}
}
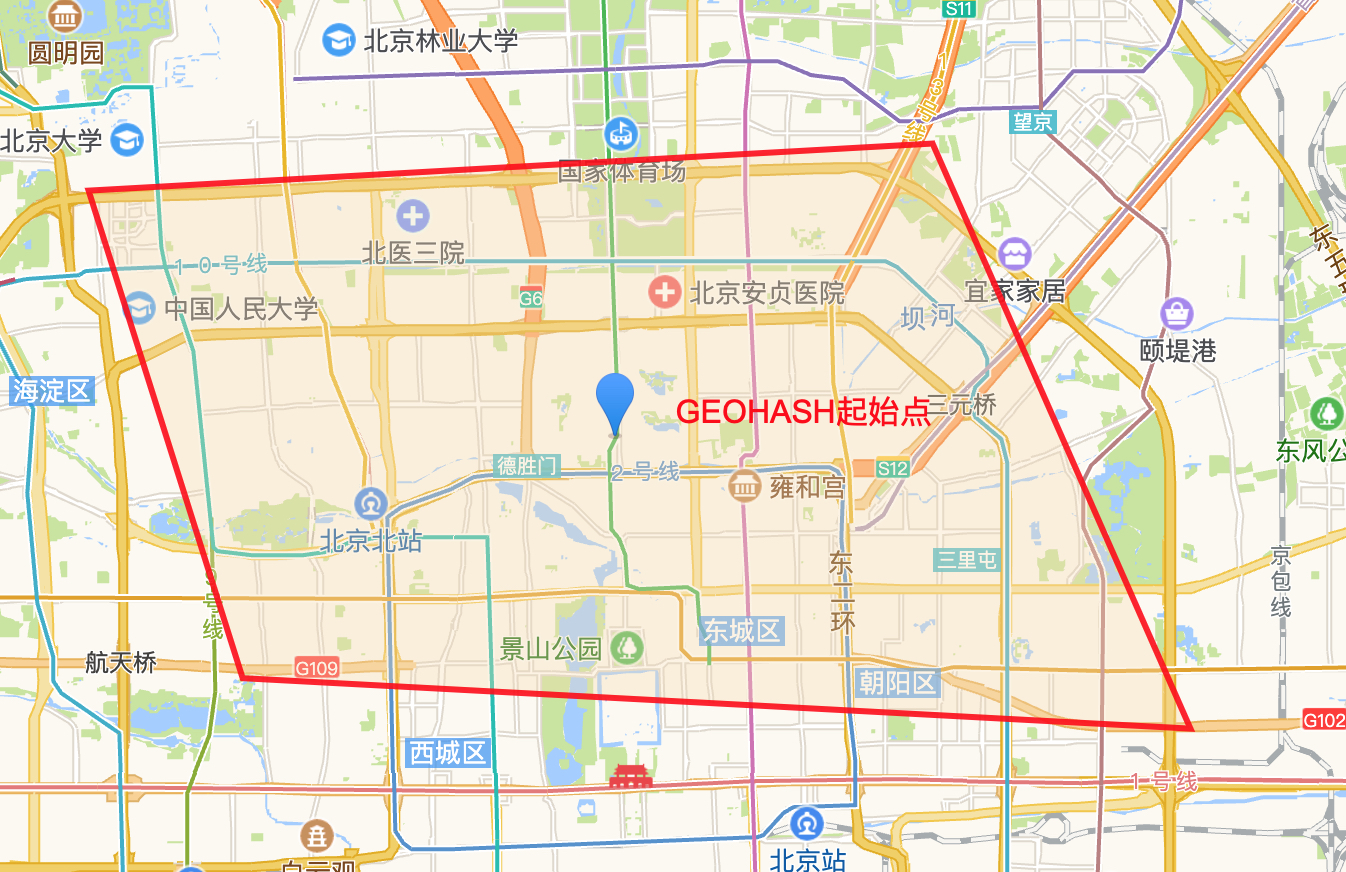
基于上文求出的中心点生成geohash,并且生成它的8个neighbors
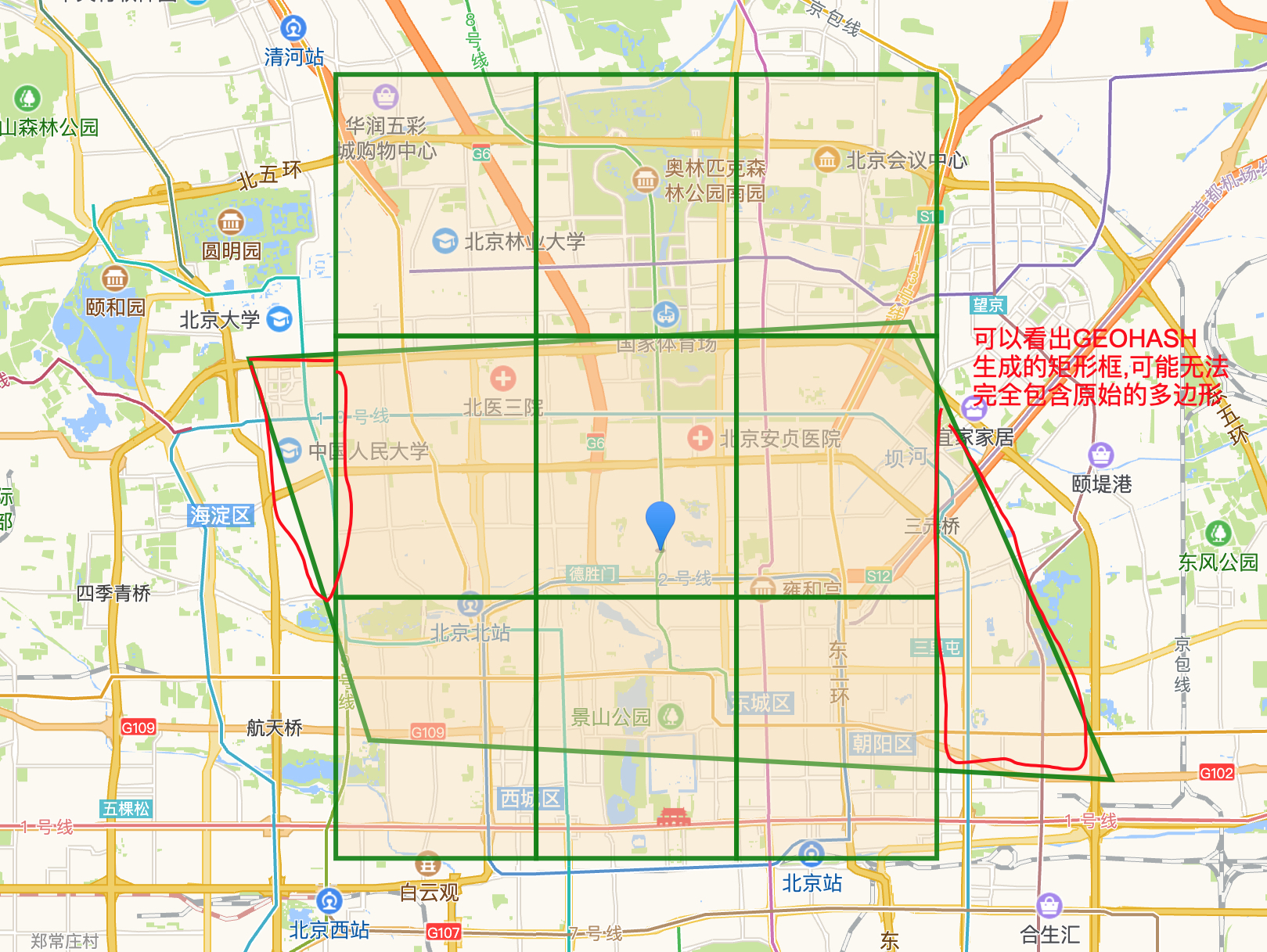
geohash具体方法就不自己实现了,直接基于github.com/mmcloughlin/geohash库来使用
func GenerateGeohash(point []float64, level int) {
// 生成geohash值
originGeoHash := geohash.Encode(point[1], point[0])
// 得到geohash对应等级的scope
box := geohash.BoundingBox(originGeoHash[:level])
result := generatesJsFile(generate(box))
// 得到geohash的8个neighbors
str := geohash.Neighbors(originGeoHash[:level])
for _, v := range str {
// 获取neighbors的scope
box := geohash.BoundingBox(v)
}
}
判定流程图
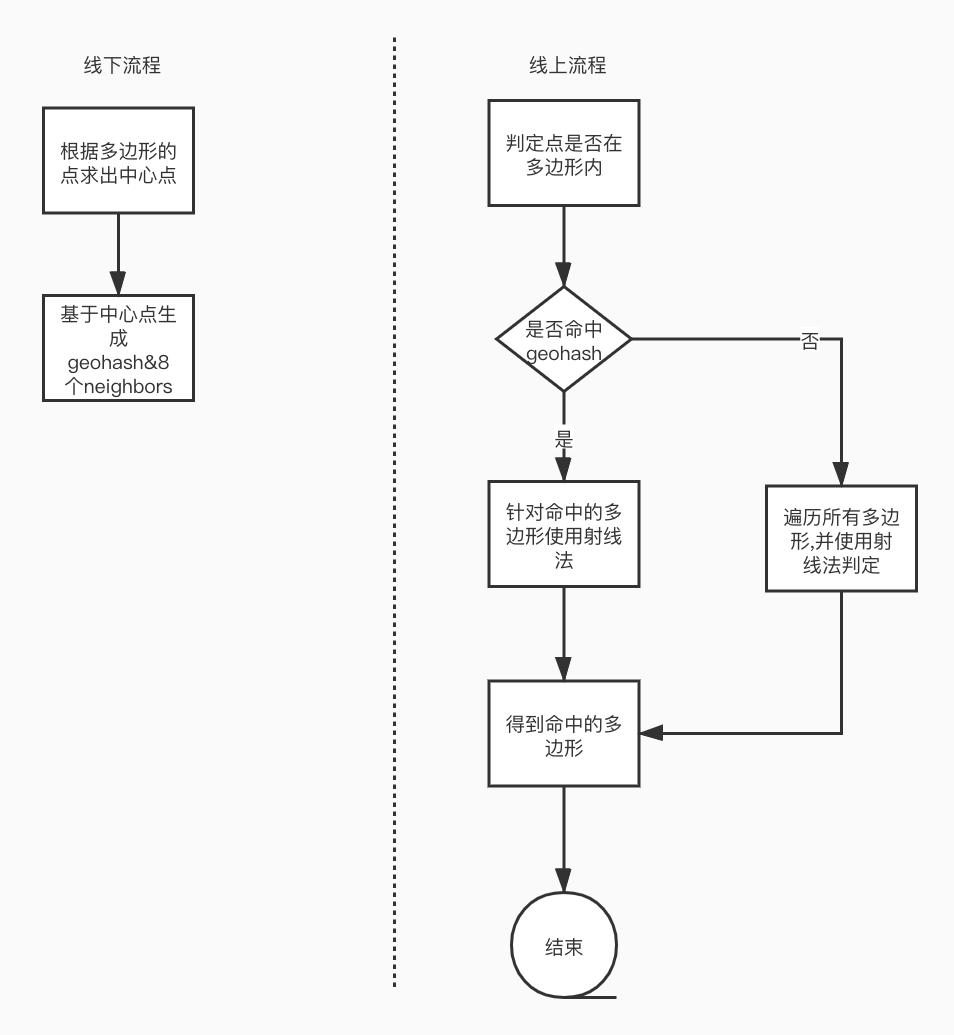
优缺点
- 优点:使用空间索引有效的减少了判定是否在商圈内射线法的使用次数。
- 缺点:对于一些边界
case还是没有办法完全解决,可能仍需遍历全部商圈进行判定
阶段0X03 结合空间索引采用切格子方式进行高效判定
上述已经描述了,阶段0X02会存在一些缺点,比如生成的geohash的bounding-box无法包含住多边形,可能仍需采用几何算法进行全部商圈的遍历。
那么有没有什么办法能够将生成的bounding-box完全铺满多边形呢?
针对于这种场景,我们不妨先生成多边形的MBR,基于此求出多边形与geohash的交集与非交集
最小外接矩形(MBR)
最小外接矩形(minimum bounding rectangle,MBR),译为最小边界矩形
MBR
// 求最小外接矩形
type Rectangle struct {
MaxLat float64
MinLat float64
MaxLng float64
MinLng float64
}
// 生成四个值
func GetMinRectangle(data [][]float64) Rectangle {
maxLat, maxLng := float64(-1<<32), float64(-1<<32)
minLat, minLng := float64(1<<32), float64(1<<32)
for _, v := range data {
maxLat = math.Max(maxLat, v[1])
maxLng = math.Max(maxLng, v[0])
minLat = math.Min(minLat, v[1])
minLng = math.Min(minLng, v[0])
}
r := &Rectangle{
MaxLat: maxLat,
MinLat: minLat,
MaxLng: maxLng,
MinLng: minLng,
}
//r = &rectangle{maxLat: maxLat, minLat: minLat, maxLng: maxLng, minLng: minLat}
return *r
}
可以看出我们得到的最小外接矩形如下图:
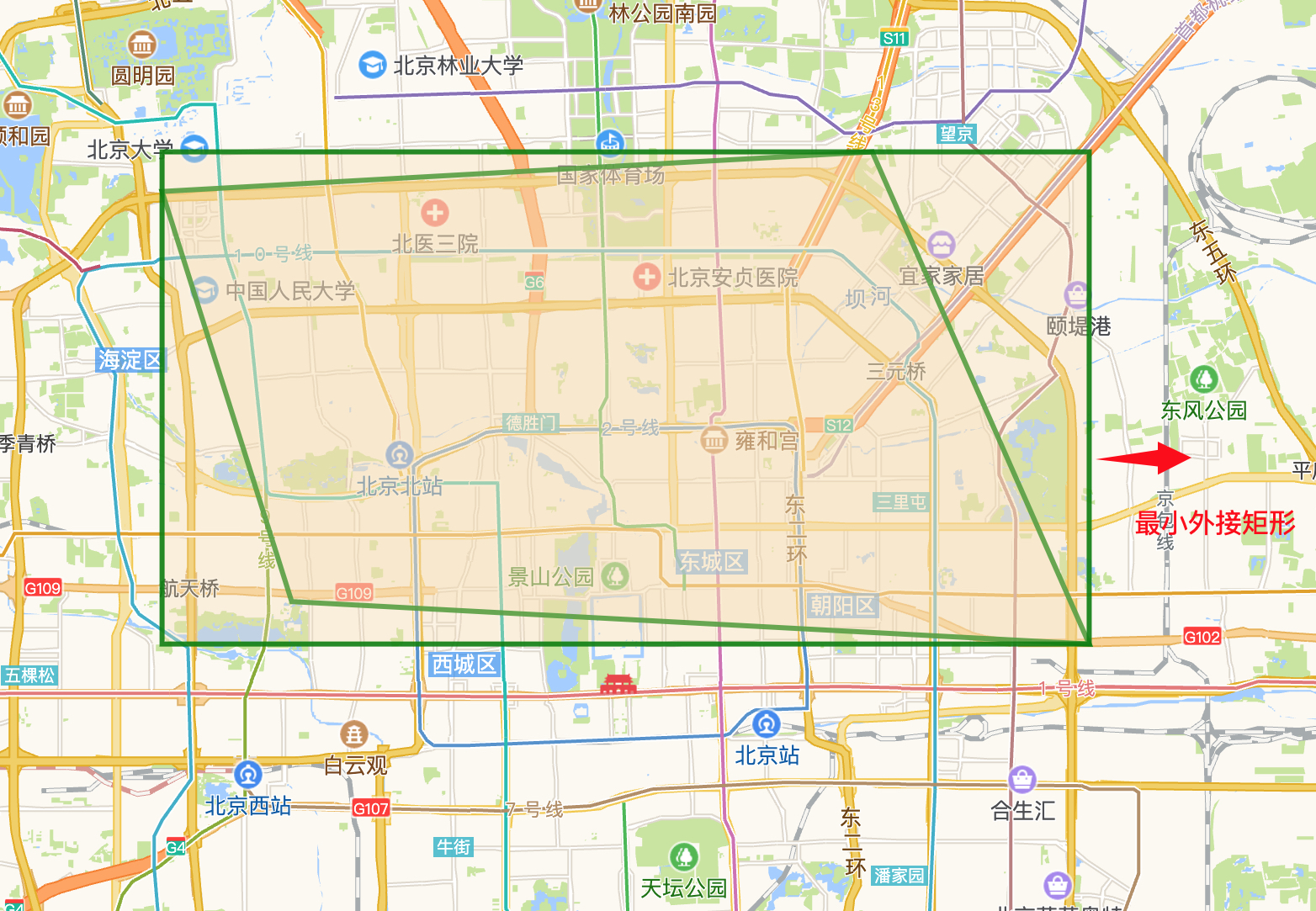
然后我们基于生成的MBR,以最左上角顶点为例(minLng,maxLat),生成该点的geohash,并且求出该点的bounding-box [简称为格子],生成的格子如下图:
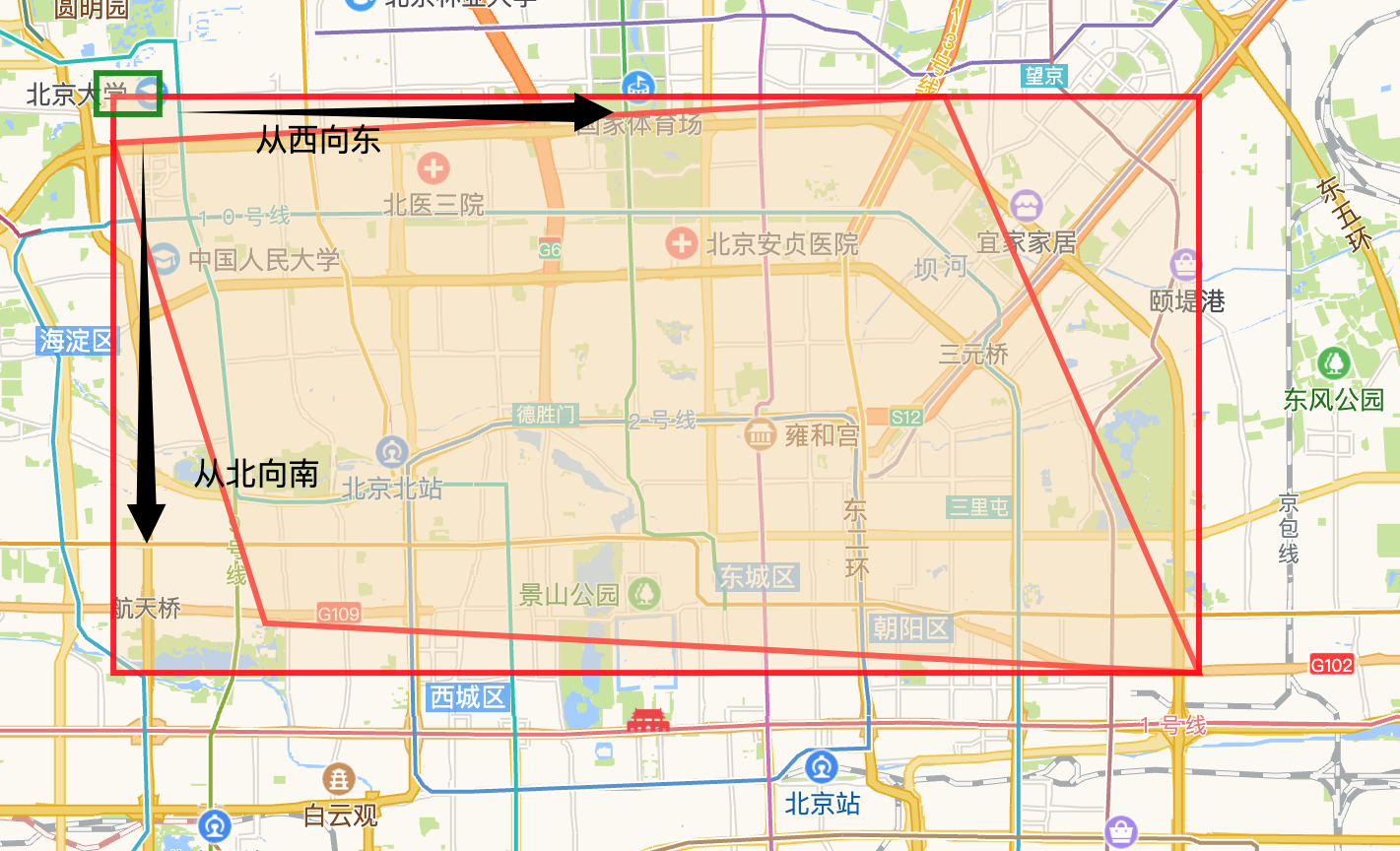
如何求出顶点格子的neighbor?
拿左上角顶点为例,我们已经得到了这个顶点格子的bounding-box
- 通过
geohash-neighbor拿到这个格子的东侧格子的bounding-box - 求出
neighbor东侧格子的中心经纬度 - 基于得出的东侧格子再次向右重复求解
最后就可以使用geohash生成的Bounding-Box,基于递归来将整个多边形完全覆盖。
递归终止条件为:
- X轴,生成的
geohash bounding-box的Lng小于MBR的maxLng - Y轴,生成的
geohash bounding-box的Lat大于MBR的maxLat
golang相关代码实现
// Y轴生成的geohash-bounding-box是否满足条件
func GenerateGridList(lat, lng float64, maxLng float64, maxLat float64, level int64) {
if lat < maxLat {
return
}
// 1.这里的操作是将传入的初始值,计算成bounding box
originGeoHash := geohash.Encode(lat, lng)
// 递归执行
recursion(lat, lng, maxLng, level)
boundingBox := ProduceBoundingBox(lat, lng, SOUTH, level)
lat, lng = boundingBox.Center()
GenerateGridList(lat, lng, maxLng, maxLat, level)
}
// 生成geohash bound-box
func ProduceBoundingBox(lat, lng float64, direction, level int64) geohash.Box {
originNorthPointGeoHash := geohash.Encode(lat, lng)
neighbors := geohash.Neighbors(originNorthPointGeoHash[:level])
return geohash.BoundingBox(neighbors[direction])
}
// 横向结构递归执行(X轴)
func recursion(lat, lng float64, maxLng float64, level int64) {
if lng > maxLng {
return
}
boundingBox := ProduceBoundingBox(lat, lng, EAST, level)
PolygonContains(boundingBox, false)
lat, lng = boundingBox.Center()
recursion(lat, lng, maxLng, level)
}
最后我们得到了由许多格子完全覆盖MBR的一个集合,如下图:
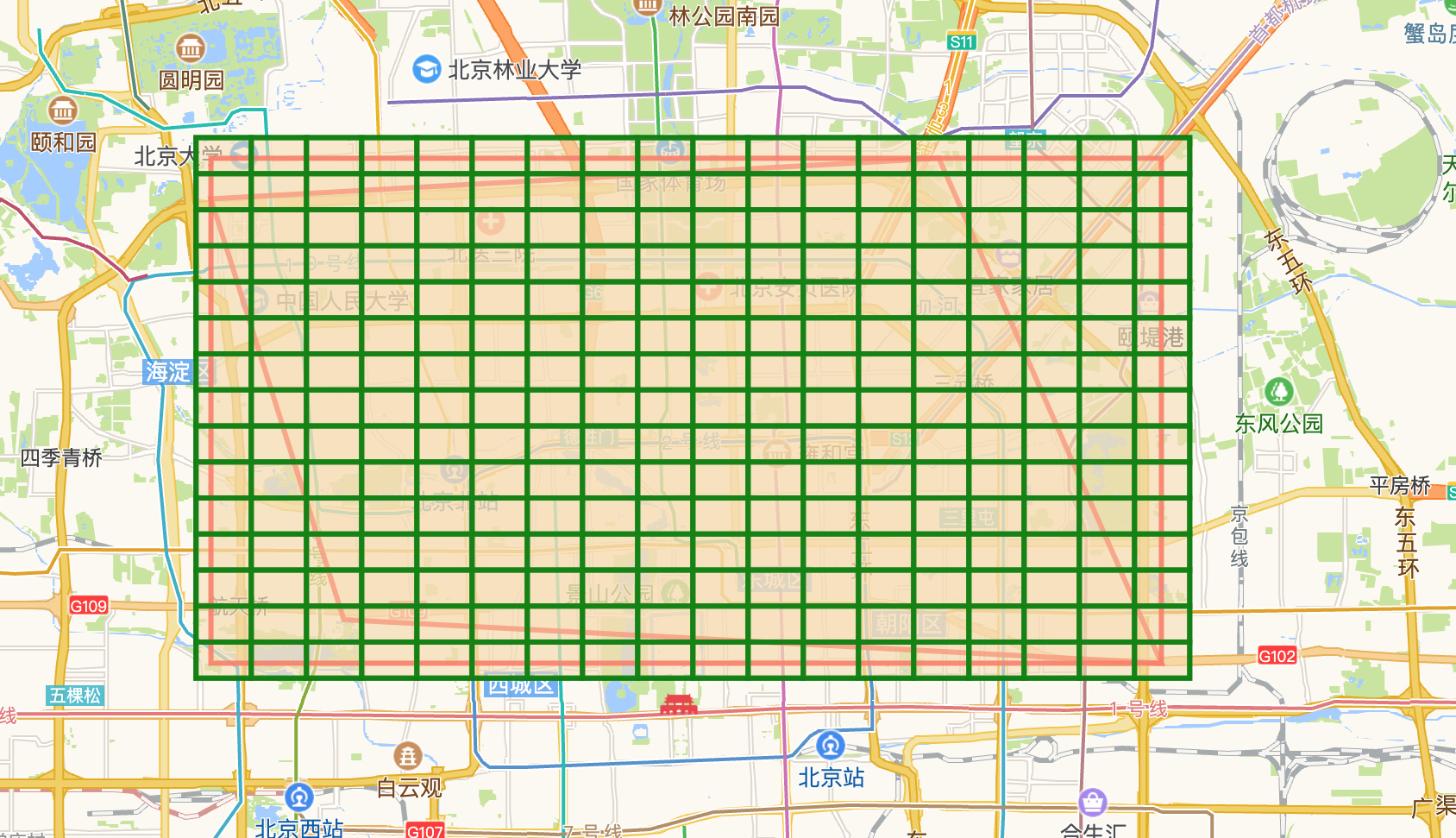
处理多边形与矩形不相交的部分
我们可以看出此时还是有一些与原始的多边形不相交的矩形,对于我们来说是干扰项,那么如何把这些干扰项去掉呢?
实际上我们只需要认为矩形的四个点,刚好都不在原多边形内,则认为与之不相交
解决方案:
我们只需要上述实现的射线法,判定矩形的四个点是否在多边形内,若都不在则不相交。
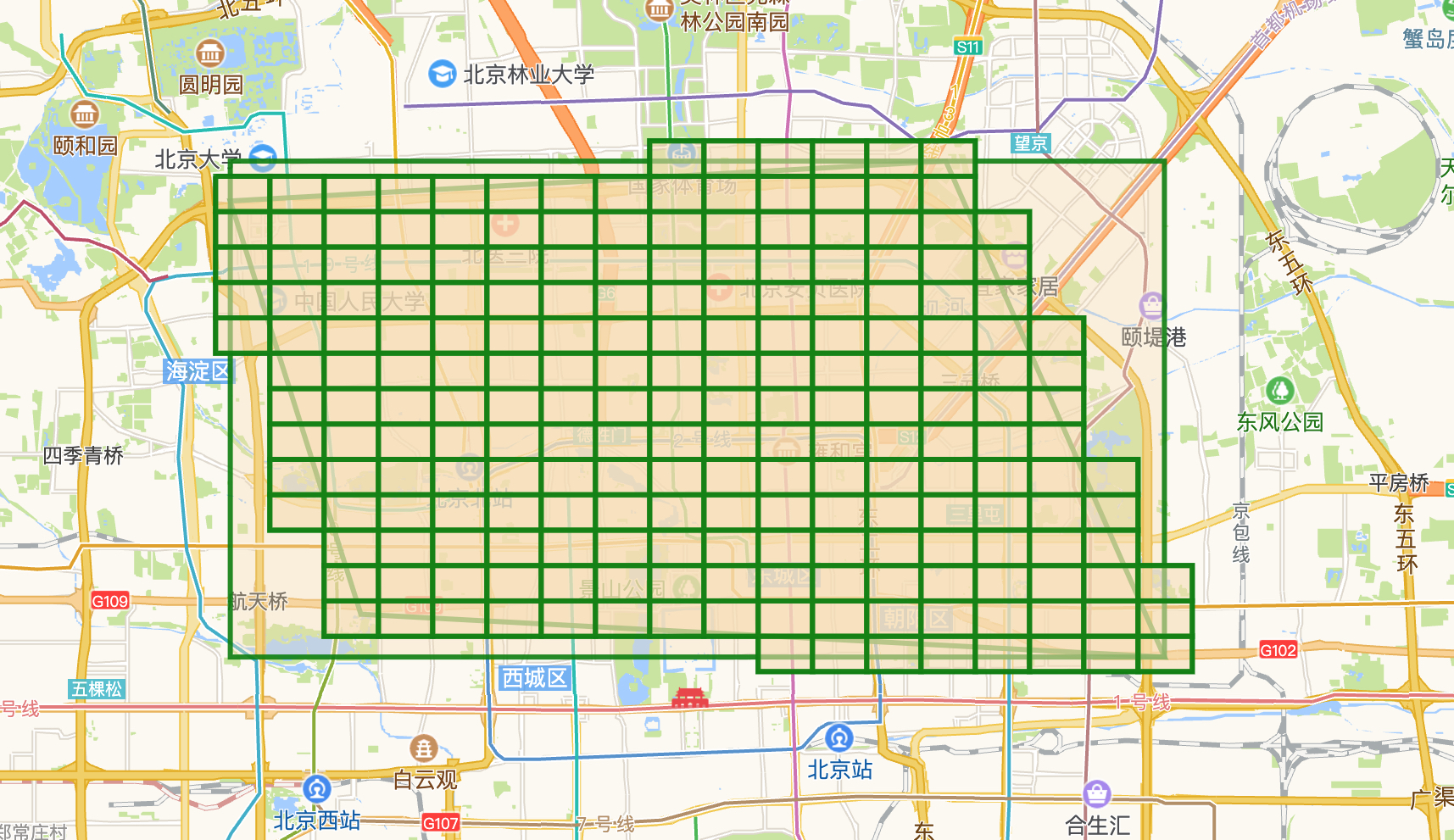
处理多边形与矩形的交点部分
从上述图中可以看出,还有一些格子部分是在多边形内部,部分在多边形内部,我们实际上只需要在多边形内部的部分,既然需要内部部分,那么需要先求出多边形与格子的交点。
如何来求多边形与矩形格子的交点呢?实际上可以抽象为线段与矩形的交点,最后抽象为多边形线段与矩形线段的交点。
根据两点式公式:
( y - y1 ) / ( y2 - y1 ) = ( x - x1 ) / ( x2 - x1 )
推导出:
y = [ ( y2 - y1 ) / ( x2 - x1 ) ]( x - x1 ) + y1
直线斜率为:
k = ( y2 - y1 ) / ( x2 - x1 )
需要考虑的是矩形的两条线段,一条平行于X轴,一条平行于Y轴。
// 求线段与线段交点
func GetIntersectionPoint(LineFirstStart Point, LineFirstEnd Point, LineSecondStart Point, LineSecondEnd Point) (*Point, error) {
a := (LineFirstEnd.Y - LineFirstStart.Y) / (LineFirstEnd.X - LineFirstStart.X)
b := Decimal(LineSecondEnd.Y-LineSecondStart.Y) / Decimal(LineSecondEnd.X-LineSecondStart.X)
point := Point{}
if math.IsInf(b, 0) {
// b的斜率为0
x := LineSecondStart.X;
y := (LineFirstStart.X-x)*(-a) + LineFirstStart.Y
point = Point{
X: x,
Y: y,
}
return &point, nil
}
x := (a*LineFirstStart.X - b*LineSecondStart.X - LineFirstStart.Y + LineSecondStart.Y) / (a - b)
y := a*x - a*LineFirstStart.X + LineFirstStart.Y
point = Point{
X: Decimal(x),
Y: Decimal(y),
}
return &point, nil
}
实际上,上述公式是拿直线进行计算的,但是我们是线段,所以需要拿矩形的bounding-box的范围来限制一下
// 检查交点是否落在矩形范围内
func checkPointRange(point Point, rectangle [][]float64) (*Point, error) {
r := GetMinRectangle(rectangle)
if point.X > (r.MaxLng) || point.X < (r.MinLng) || point.Y > (r.MaxLat) || point.Y < (r.MinLat) {
return nil, errors.New("error happen")
}
return &point, nil
}
构造新的多边形
通过上述操作已经拿到了多边形与矩形的交点,那么我们就可以认为多边形与矩形相交场景下,矩形点所在多边形内与求出的交点可以求出新的多边形。
顺序问题
因为题头也说过了,多边形实际上是按照顺时针或者逆时针顺序排列的,当顺序出错的时候可能得到不是我们想要的多边形,所以顺序是需要考虑的一个问题。
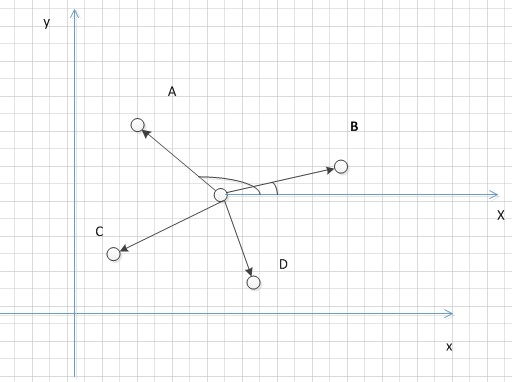
解决方案:
-
首先计算出来多边形的重心
-
以重心O作一条平行于X轴的单位向量OX,然后依次计算OPi和OX的夹角,根据夹角的大小,确定点之间的大小关系。
具体代码如下:
func PointCmp(pointA []float64, pointB []float64, center []float64) bool {
if pointA[0] >= 0 && pointB[0] < 0 {
return true
}
if pointA[0] == 0 && pointB[0] == 0 {
return pointA[1] > pointB[1]
}
det := (pointA[0]-center[0])*(pointB[1]-center[1]) - (pointB[0]-center[0])*(pointA[1]-center[1])
if det < 0 {
return true
}
if det > 0 {
return false
}
d1 := (pointA[0]-center[0])*(pointA[0]-center[0]) + (pointA[1]-center[1])*(pointA[1]-center[1]);
d2 := (pointB[0]-center[0])*(pointB[0]-center[1]) + (pointB[1]-center[1])*(pointB[1]-center[1]);
return d1 > d2;
}
func ClockwiseSortPoints(polygon [][]float64) [][]float64 {
//计算重心
center := make([]float64, 2)
x := float64(0)
y := float64(0)
for i := 0; i < len(polygon); i++ {
x += polygon[i][0];
y += polygon[i][1];
}
center[0] = x / float64(len(polygon))
center[1] = y / float64(len(polygon))
//冒泡排序
for i := 0; i < len(polygon)-1; i++ {
for j := 0; j < len(polygon)-i-1; j++ {
if (PointCmp(polygon[j], polygon[j+1], center)) {
tmp := polygon[j];
polygon[j] = polygon[j+1];
polygon[j+1] = tmp;
}
}
}
return polygon
}
顶点处理
当多边形的点位于格子内的时候,此时需要特殊处理。
首先需要定位到哪些是格子的顶点?实际上组成多边形的点都是在格子内的顶点。
那么如何来根据顶点构造新的多边形呢?
解决方案
- 使用射线法判定多边形的点是否在格子内(求出顶点)
- 先求出格子顶点所在线段与多边形的交点
- 最后带入到顶点线段里面,看范围是否符合
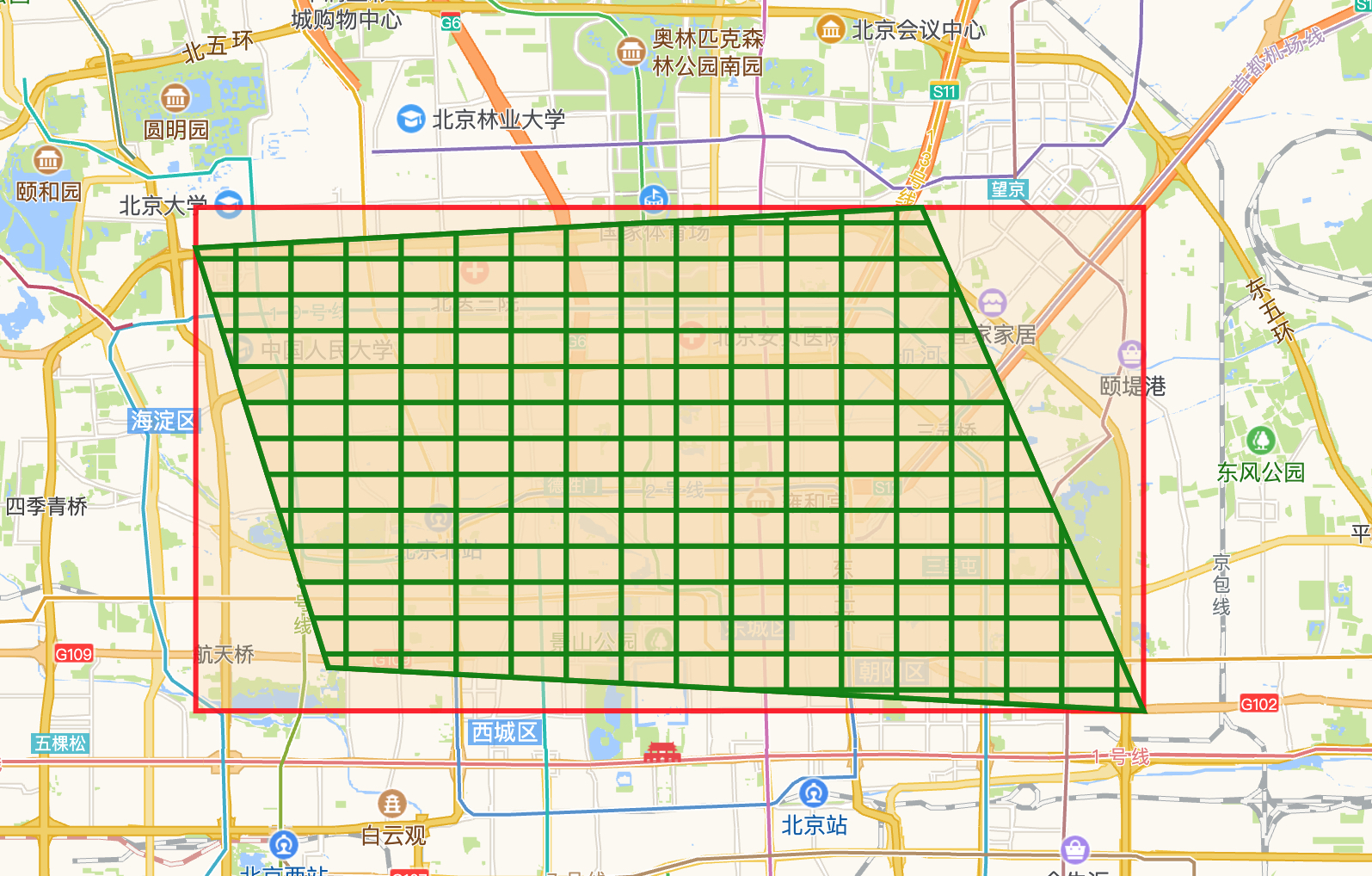
最后我们得出了我们想要的格子完全覆盖多边形的图
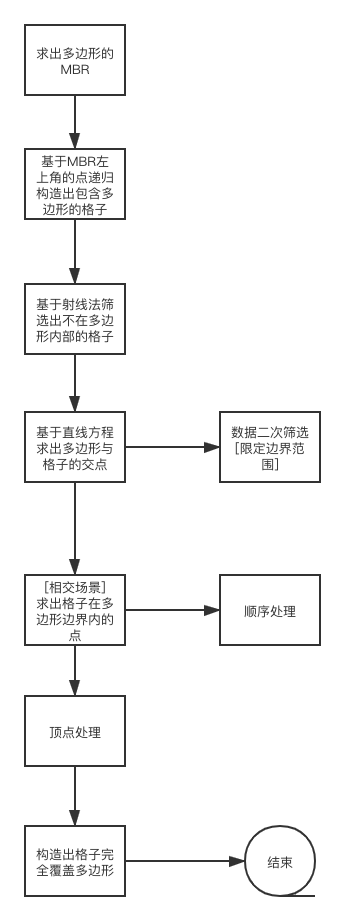
判定流程图
两种使用方式
基于递归生成:
首先,我们保留格子包含于多边形内的格子,然后将我们求出的新多边形(格子与多边形相交),在求一次MBR,然后选取适当的geohash长度,重复上述步骤。
直接使用: 在写程序的时候,可以将格子标记为三种状态
- 格子在多边形内
- 格子在多边形外
- 格子在于多边形相交
根据用户上报上来的经纬度进行geohash后进行分类,
- [格子在多边形内]直接返回商圈信息
- [格子在多边形外]点与多边形相交,进行一次射线法
- [格子在多边形外]点不在所有格子内,返回不存在