一.选择排序
时间复杂度: O(n²)
选择排序就是不停地选择最小的数放到最前面,然后再对后面的数做同样的事情
算法 : 先假设并取第一个数为最小值,然后与后面的每个数进行比较,并把比较后的最小值放到数组最前。然后对后面的数进行排序,对后面的数进行排序时把最小的数提到前面来;然后再对后面的数进行排序,对后面的数进行排序时再把最小的数提到前面,... ,直到后面的数只剩下两个,最后假设倒数第2个值为最小值,并与倒数第一个数比较大小即可。
let minIndex=(numbers)=>{ //minIndex函数找出并返回每次比较时最小值的下标
let index=0
for(let i=1;i<numbers.length;i++){ //从数组第二个数开始遍历
if(numbers[i]<numbers[index]){
index = i //贪心算法,遍历时只要遇到比自己小的就赋给自己
}
}
return index
}
let swap=(array,i,j)=>{
let temp=array[i]
array[i]=array[j]
array[j]=temp
}
let sort=(numbers)=>{
for(let i=0;i<numbers.length-1;i++)
//设数组有五个数,因第四个数要跟第五个数比大小,故循环到数组的第四个数即可,所以是长度减1.
//从数组第一个数开始循环,到数组的倒数第二个数(下标为numbers.length-2)结束.
//最后一个数(下标为numbers.length-1)不用参与循环.
//共比较大小numbers.length-1次
//共选择numbers.length-2次最小值(第一个值和最后一个值不用选)
{
console.log(`----------`)
console.log(`i: ${i} ,第${i+1}次比较`)
let index=minIndex(numbers.slice(i))+i
//minIndex返回的是当前减掉i个值的数组的最小值下标,要把减掉的下标加回来才是相对整个参与排序的数组的下标,所以在这里要加回i
console.log(`最小值下标index为: ${index}`)
console.log(`最小值min为: ${numbers[index]}`)
if(index!==i){
swap(numbers,index,i)
console.log(`下标为${index}的值与下标为${i}的值交换位置`)
console.log(numbers)
}//整个参与排序的数组中,下标为index和下标为i的两个值交换位置
}
return numbers
}
PS:如果是从大到小排序,把minIndex里的numbers[i]<numbers[index]改成numbers[i]>numbers[index]即可。
二.快速排序
时间复杂度 : O(nlogn)
算法 : 每次随机指定一个没指定过的数(这个数就是基准),把比这个数小的熟放到这个数的前面,把比这个数大的数放到后面。
let quickSort=(numbers)=>{
if(numbers.length<=1){
return numbers
}
let pivotIndex=Math.floor(numbers.length/2)
//获取基准值下标 Math.floor():往下找一个最靠近的整数
let pivot=numbers.splice(pivotIndex,1)[0]
//获取基准值.把基准值从数组中删出来.
let left=[]
let right=[]
for(let i=0;i<numbers.length;i++){ //遍历已经去掉了基准值的数组
if(numbers[i]<pivot){
left.push(numbers[i])
}else{
right.push(numbers[i])
}
}
return quickSort(left).concat([pivot],quickSort(right))
//对左边和右边进行快速排序,左边排好序的数组+基准值+右边排好序的数组
}
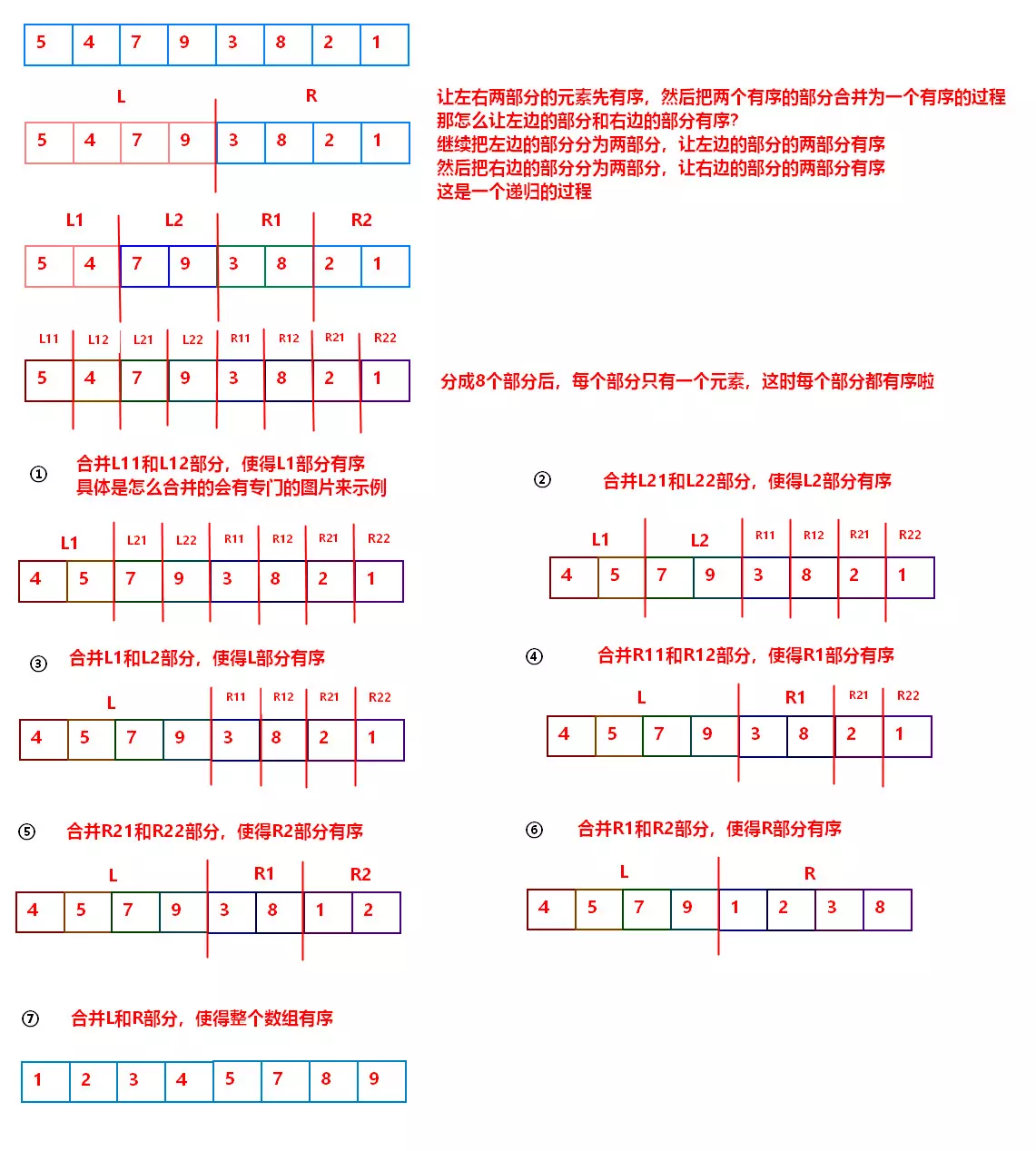
三.归并排序
归并排序(Merge)是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
算法 : 不设定基准值,把数组分成左右两边,再把左右两边的数组中的每个值单独拆成只有一个数的数组,再从少到多进行排序并合并。归并算法只会把两个排好序的数组合并起来。PS:归并排序中的每个数组均为已排好序的数组。
时间复杂度:O(nlogn)
let mergeSort = arr =>{
if(arr.length===1){return arr}
let left = arr.slice(0, Math.floor(arr.length/2))
let right = arr.slice(Math.floor(arr.length/2))
return merge(mergeSort(left), mergeSort(right))
}
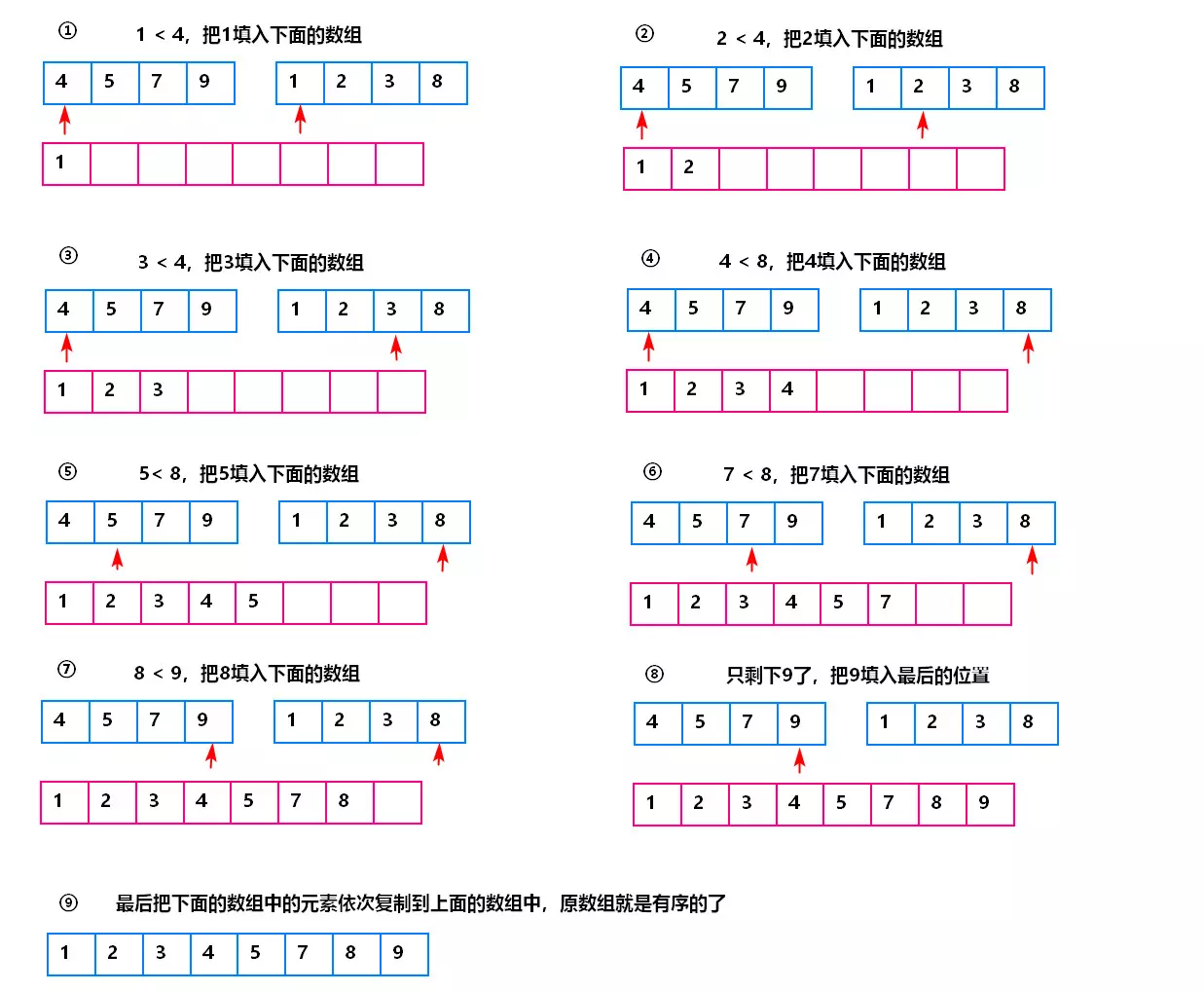
let merge = (a, b) => {
if(a.length === 0) return b
if(b.length === 0) return a
return a[0] > b[0] ?
[b[0]].concat(merge(a, b.slice(1))) :
[a[0]].concat(merge(a.slice(1), b))
}
归并算法具体图示:
四.计数排序
时间复杂度:O(n+max)
计数排序需要一个额外的哈希表做记录!
计数排序类似于给扑克牌排序,先把四张同大小的扑克牌放在一起,再将牌堆按大小排序即可.
算法:先把所有值和其出现的次数记在哈希表中,在记的同时找出已出现的数的最大值。然后再从0开始到最大值遍历哈希表,如果有相应的值就按已记录的次数打印到一个新的数组中,没有则跳过该值。(比如:有一个数组[2,6,1,0,9,4,8,11,15,12],则遍历0,1,2,...,15)
思路:
1.用一个哈希表做记录.
2.发现数字n就记n:1,如果再次发现n就加上1变成n:2,以此类推.
3.最后把哈希表中的key全部打出来,再按value的值决定打印key的次数.假设有n:4,则n需要打印4次.
let countSort=(numbers)=>{
let hashTable={}
let max=0
let result=[] //建立新的哈希表,最大值和需要存放结果的数组
for(let i =0;i<numbers.length;i++){ //开始遍历数组
if(!numbers[i] in hashTable){
hashTable[numbers[i]]=1
}else{
hashTable[numbers[i]]+=1
} //将未在哈希表中存在的数记录进哈希表并设定出现次数为1,不是第一次出现就再加1.
if(numbers[i]>max){
max=numbers[i]
}
} //遍历数组并记录进哈希表中,并找出数组中的最大值.得到哈希表和max.
for(let j=0;j<=max;j++){ //开始遍历哈希表,j代表哈希表中的每个key
if(j in hashTable){
for(let i=0;i<hashTable[j];i++){ //再次遍历哈希表,要拿到j的value才能决定打印几次j
result.push(j)
}
}
}
}