快速幂(笔记)

快速幂

所谓的快速幂，就是为了快速的求幂。 一种将时间复杂度从朴素算法O(n)降到O(logn)求幂的算法 快速幂的原理: a ^ b 其实指数b是可以拆成二进制的。 通过公式

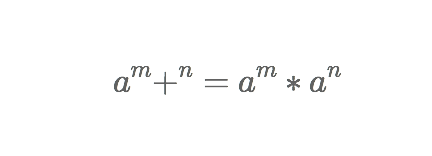
我们可以发现,一旦指数b拆成2进制,那么a ^ b 也可以进行相应的拆分。 例如: 当b=11,b的二进制位1011,即11 = 1 * (2 ^ 0) + 1 * (2 ^ 1) + 1 * (2 ^ 3); 那么(a ^ 11) = a * (1 * (2 ^ 0) + 1 * (2 ^ 1) + 1 * (2 ^ 2)) 等价于 (a ^ 1) * (a ^ 2) * (a ^ 8); 每位代表的十进制：

朴素算法 O(n)

// a = 5,b = 12 loopCount = 12
int pow(int a,int b) {
    int res = a;
    while(b) {
        res = res * a;
        b--;
    }
    return res;
}

快速幂模板 O(logn)

int pow(int a,int b) {
    int res = 1;
    while(b) {
        if(b & 1) {
            res = res * a;
        }
        a = a * a;
        b = b >> 1;
    }
    return res;
}

模板分析

Code C++:

#include<iostream>
using namespace std;
// a = 5,b = 12 loopCount = 4
int pow(int a,int b) {
    int res = 1;
    while(b) {
         // 在二进制中找1 
        if(b & 1) {
            res = res * a;   // 位数是1的时候就会累加
        }
        a = a * a; // a ^ a; // 这里只要循环在循环就会更新
        b = b >> 1; // 右移往继续往左找
    }
    return res;
}
 
/*  
 5 ^ 12 = 244140625
        6 = 1100,位数是1的数分别代表(8,4)
        5 ^ 6 = (5 ^ 8) * (5 ^ 4);

        5 ^ 8 = 390625
        5 ^ 4 = 625
        390625 * 625  = 244140625

        5^12 = 244140625
*/
int main() {
    cout << pow(5,6) << endl;
}

快速幂取模模板

Code C++:

#include<iostream>
using namespace std;
int qmi(int a,int b,int mod) {
    int res = 1 % mod;
    while(b) {
        if(b & 1) {
            res = res * a % mod;
        }
        a = a * a % mod;
        b = b >> 1;
    }   
    return res;
}

int main(){
    // 3 ^ 2 % 7
    int res = qmi(3,2,7);
    cout << res;    // out: 2 
} 

Code Java:

public class Main{
    public static void main(String[] args) {
        System.out.println(qmi(3,2,7)); // out: 2
    }
    
    private static int qmi(int a,int b,int q) {
        int res = 1 % q;
        while(b != 0) {
            if((b & 1) == 1) {
                res = res * a % q;
            }
            a = a * a % q;
            b = b >> 1;
        }
        return res;
    } 
}

problem：a^b

problem: 64位整数乘法

参考资料:https://www.jianshu.com/p/ec0b97676c3e