数据结构-线段树

线段树(Segment Tree)

什么是线段树?

线段树一些基础概念

• 注意点

  • 静态线段树[也就是我们的区间大小是固定的, 不会变化的] (这是我们学习的)

• 基本概念

  • 线段树每个节点表示一个区间
  • 线段树的根节点表示整个区间统计范围, 如[1-N]
  • 线段树的每个叶子节点表示长度为1的元区间
  • 线段树的每个节点[l, r], 它的左子节点是[l, mid], 右子节点是[mid + 1, r], 其中 mid = (l + r) / 2

• 特性

  • 每个区间的长度是区间内整数的个数
  • 叶子节点为1, 不能再分
  • 叶子节点的数目和根节点表示的区间长度相同

• 基本操作

  • 区间更新
  • 区间查询

• 应用场景

  1. 比如给一组数据, 如: [1, 2, 3, 4], 有两种操作, 操作1: 给第i个数加上x, 操作2: 数组中最大的数是什么?

  上面的问题, 通过数组可以很方便的查询到最大值, 我们只需要遍历这个空间[start, end]即可找出最大值。
  对于更新一个数, 我们就在这个数据上加上x, 如果A[i] = A[i] + x。使用数组实现该算法的缺点是什么呢?

  Q1: Query查询最大值复杂度为O(n), 更新复杂度为O(1)

  在有Q个query的情况下这样总的复杂度为O(QN), 那么对于查询来说这样的复杂度是不能接受的, 在没学习线段树之前可能没有更好的方法进行优化。

  2. 下面两个例子[区间染色, 区间查询]

为什么使用线段树

对于一类问题, 我们关心的是线段(或者区间)。

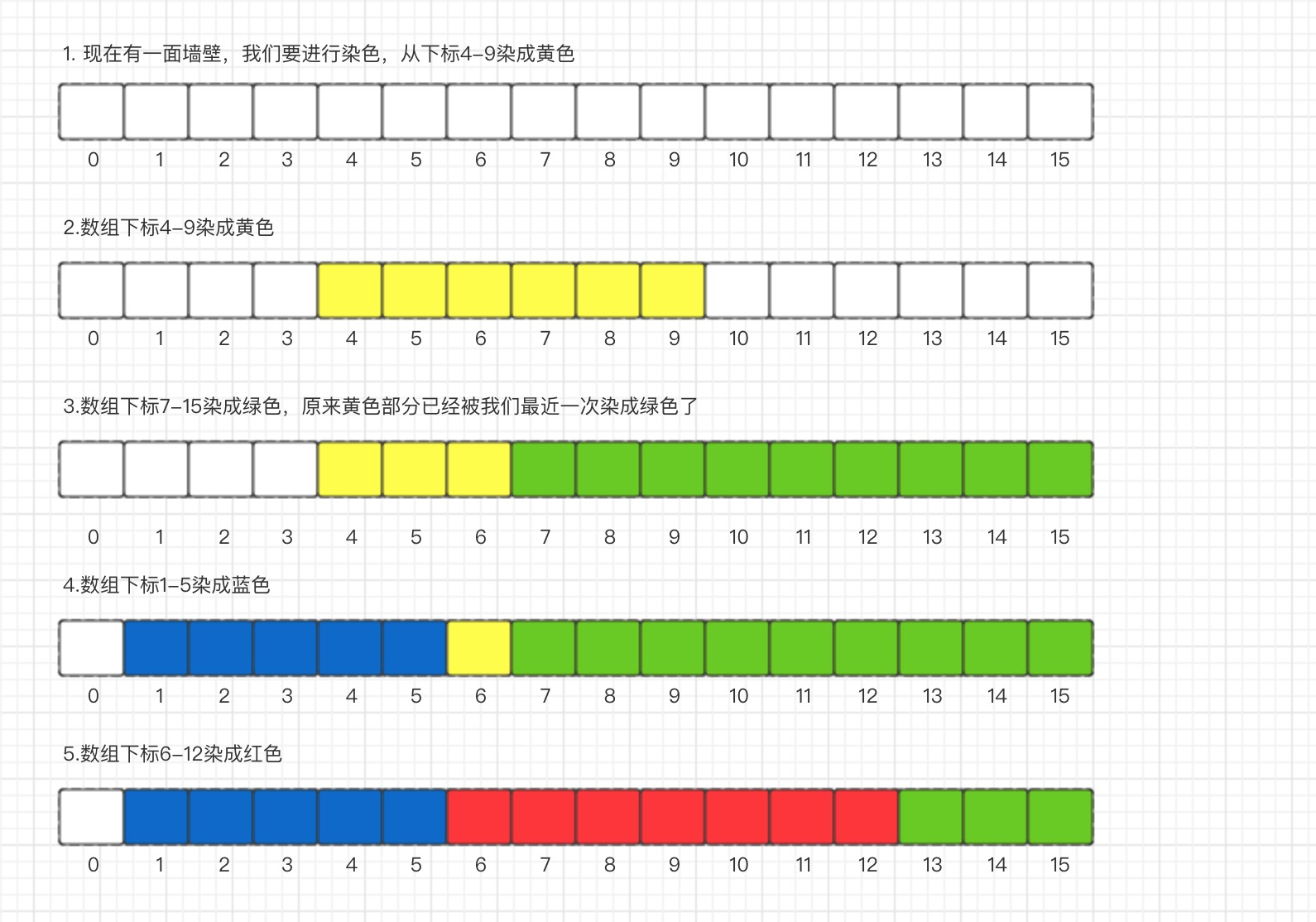
比如一个经典例子: 区间染色(如图1-1)

有一面墙, 长度为n, 每次选择一段墙进行染色。
m次操作后, 我们可以看到多少种颜色?
m次操作后, 我们可以在[i...j]区间内看到多少种颜色?

在这里, 染色操作就是我们的更新区间操作, 更新成了新的颜色。
我们在[i...j]这个区间查看有多少种颜色, 这就是查询操作。

上述问题可以通过数组来完成, 但是更新和查询的时间都是O(n)级别的, 显然这个性能是不够的。 由于我们只关注某一个区间, 此时线段树就可以派上用场了。

[图1-1]

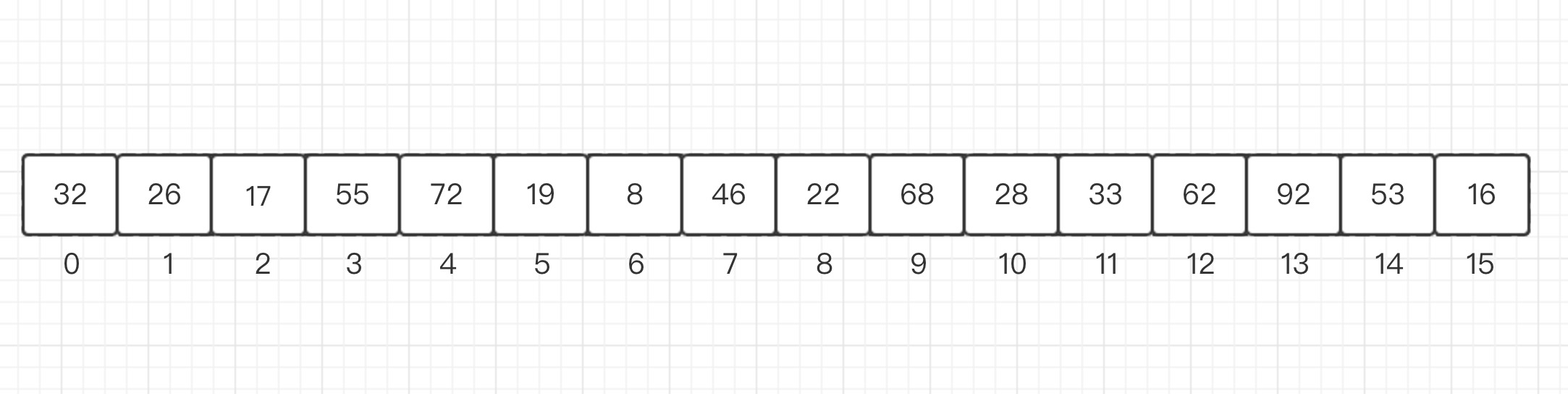
另一类经典问题: 区间查询(如图1-2)

之前我们都是针对单个元素进行插入、删除或者是更新操作。
但是, 我们有些时候希望对一个区间内的所有数据进行统计查询。
查询一个区间[i...j]的最大值, 最小值或者区间数字总和。(这就是基于一个区间的统计查询)

如: 我们现在要统计2017年注册用户截止当前消费最高的用户?消费最少的用户?

上述问题也可以使用数组来实现, 不过复杂度都是O(n)级别, 但是如果使用线段树的话则是O(logn)

[图1-2]

线段树解决以下问题: 对于给定的区间[图1-2]

1. 更新: 更新区间中一个元素或者一个区间的值
2. 查询: 查询一个区间[i...j]的最大值, 最小值, 或者区间数字和。

对于上面这些问题, 我们说都可以通过线段树来现实会更加优秀快捷。 然鹅我们构建的线段树是一个静态的, 比如上面距离的区间染色, 我们就固定在0-15这个区间内进行染色更新, 而不会去考虑这个区间会新增(如0-20), 又比如说, 我们说2017年注册用户消费, 我们就设置定在2017年内固定这个区间值, 要更新也只是这个区间范围内的值, 而不是更新这个区间的大小。

线段树的表示

我们利用数组来构建一个线段树, 如图[1-3]

[图1-3]

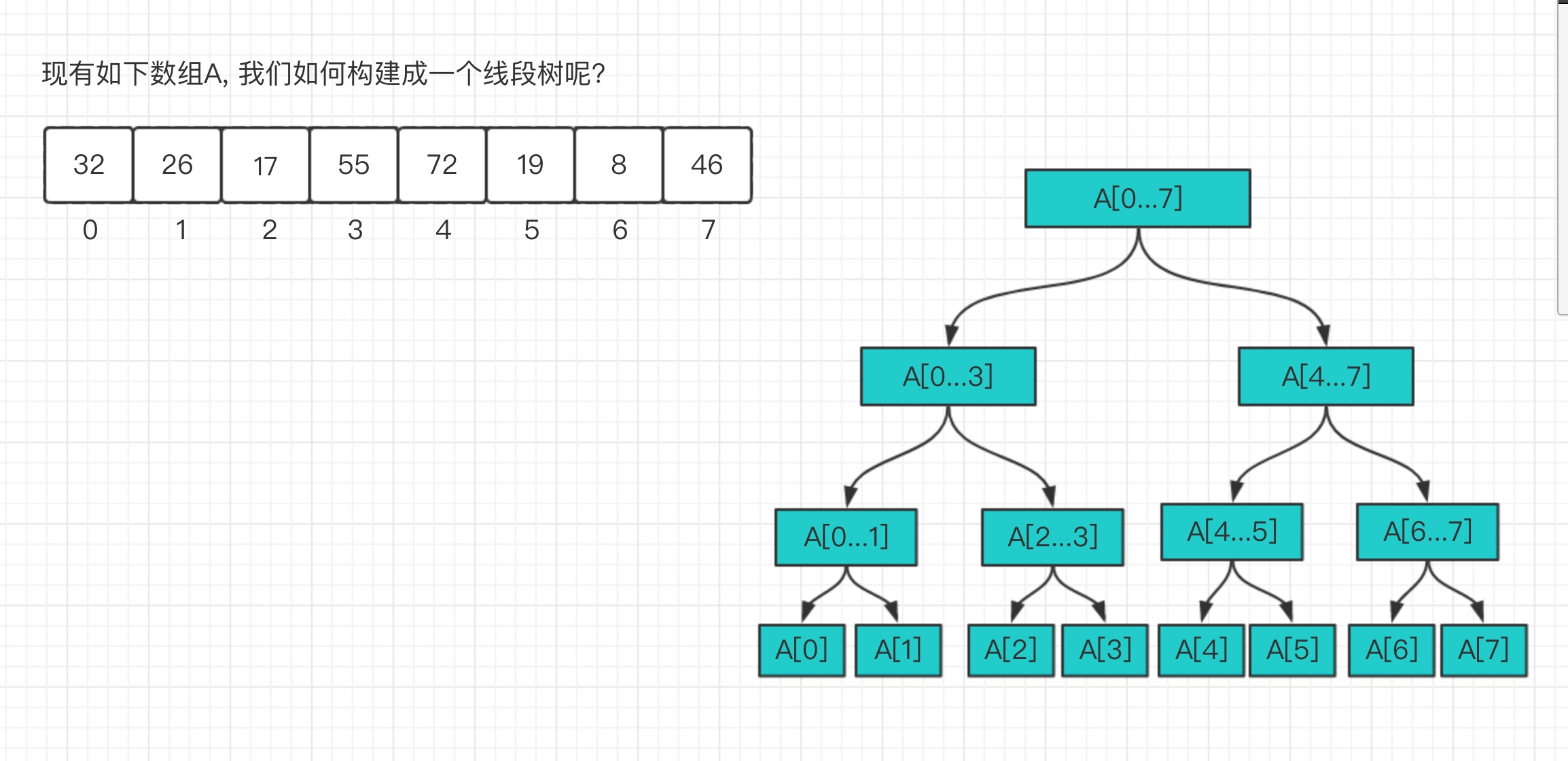
以求和为例, 我们想查询[2...5]这个区间的和, 我们需要来到A[2...3]和A[4...5]这两个节点上, 并将这两个节点的结果进行合并。如此, 当数据量非常大的时候我们依然可以通过线段树非常快的找到我们关心的区间对应的一个或者多个节点进行操作, 而不需要对这个区间中所有元素进行遍历。

线段树形态

在上面, 我们了解线段树大概是什么样子了, 但是从图1-3中我们看到线段树是一个满二叉树的形态, 只不过这个是最好的情况。

图[1-4]

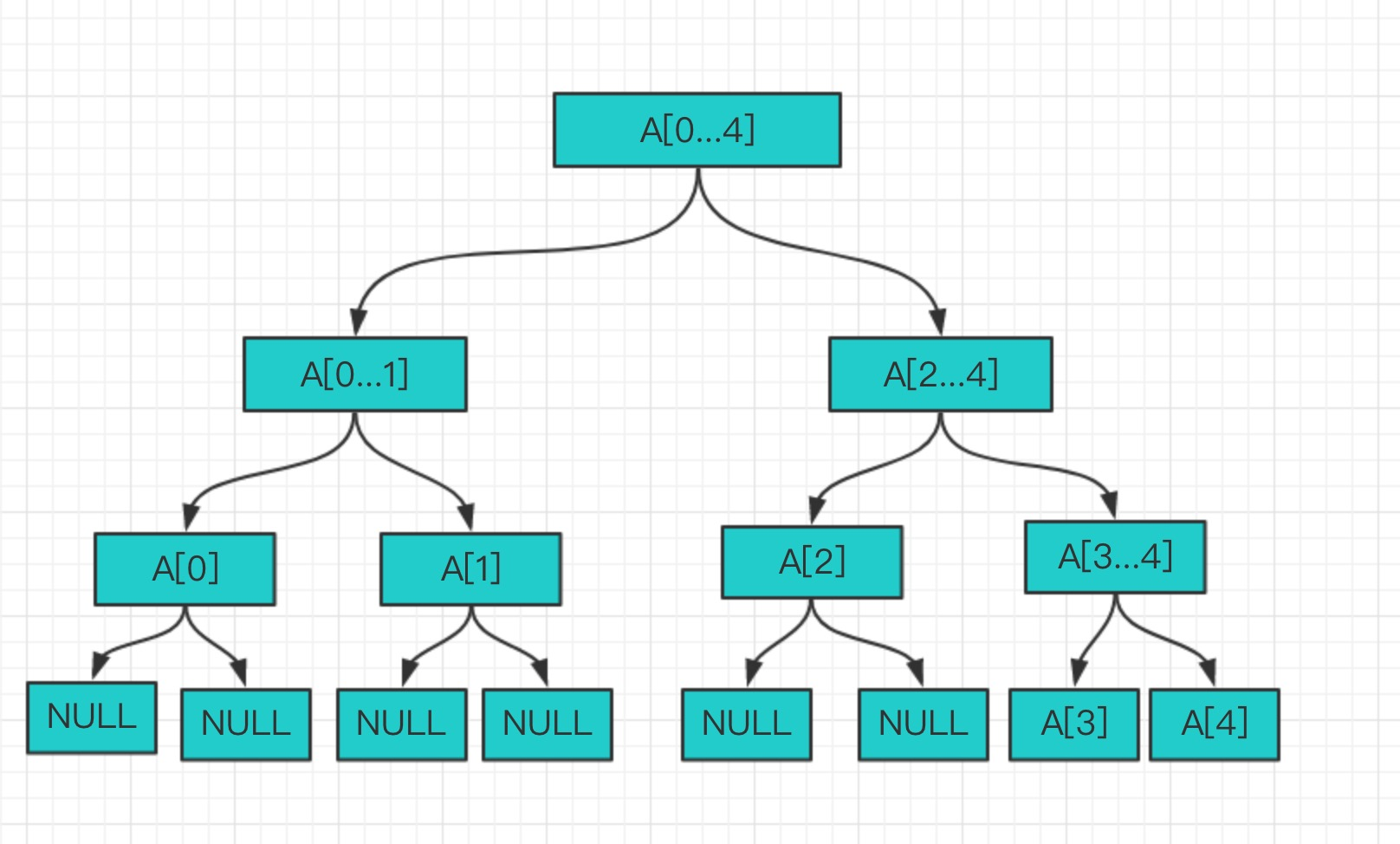
现在我们可以看到图1-4中只有5个元素, 也就得出下面的结论

• 线段树不一定是满二叉树
• 线段树不是完全二叉树
• 线段树是平衡二叉树(最大深度和最小深度之间差最多为1, 暂时先知道这个就可以)

线段树空间开辟

如果区间有N个元素, 数组表示需要多少节点?

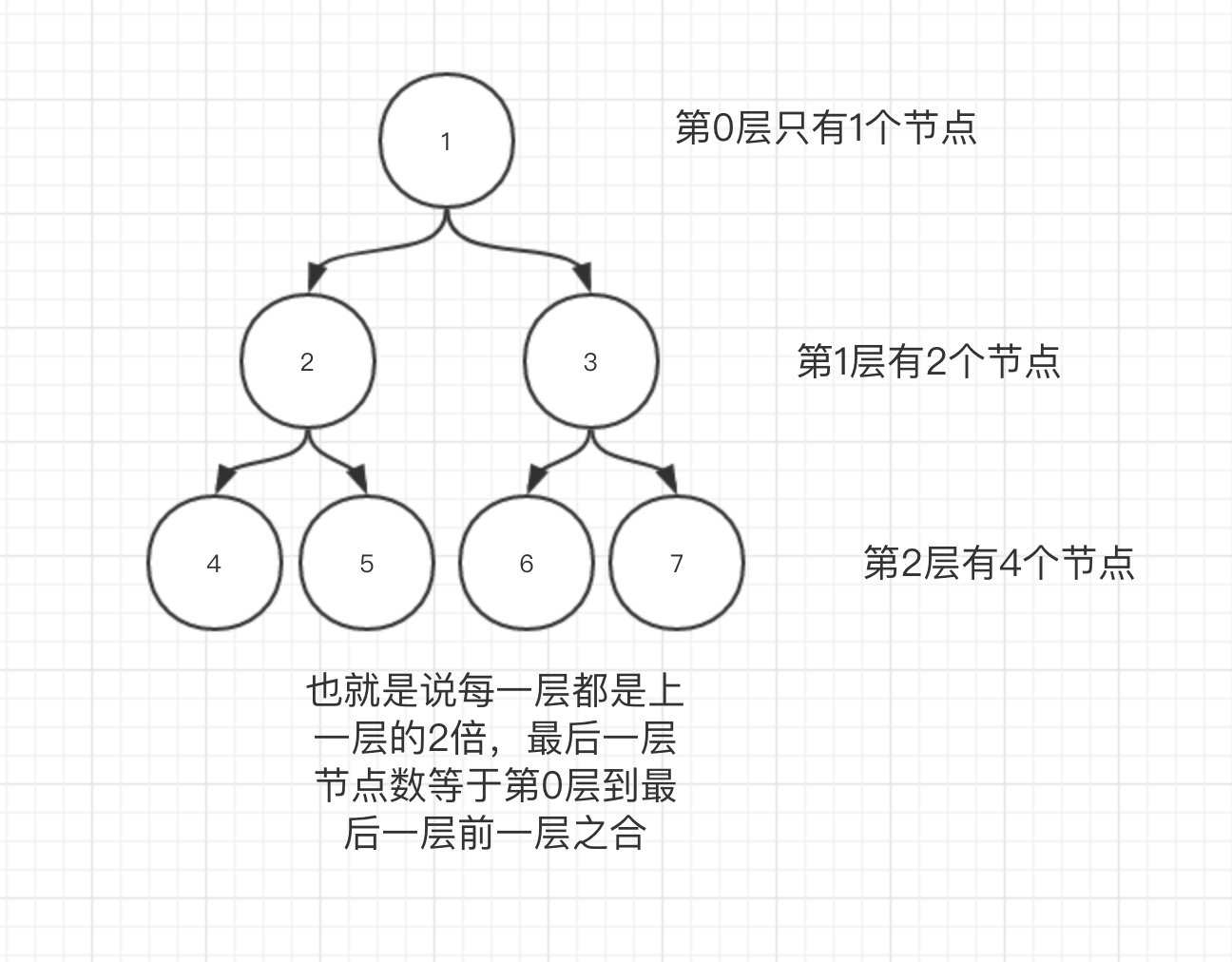
对于一个满二叉树来说, 我们第0层有1个节点, 第1层有2个节点, 第2层有4个节点, 第3层有8个节点, 第h-1层有2的h次方减1的节点。

所以一颗满二叉树我们需要的空间是2的h次方减1, 当然直接2的h次方空间即可。 也就是说满二叉树中最后一层的节点数大致等于前面所有层节点之和。

有了上面的结论, 我们回到问题需要开辟多少空呢?

假设 N=8, 或者N为2的整数次幂, 只需要2N空间

但是, 不可能N都是整数次幂, 最坏的情况2的k次方加1, 2N是不够的。如图1-4, 这个时候我们的叶子节点就是倒数的2层里面了。还需要在加一层, 所以需要4N的空间。

回到上面的概念, 线段树是一个平衡二叉树。深度不超过1。所以只会多加入一层。此时所需要的空间就是4N

上面我们也说了, 我们的线段树是静态的不考虑添加元素, 即区间固定。所以使用4N的静态空间即可。

关于4N:
其实我也看了很多别人写的4N的文章之类的, 说实话还是没看懂, 基本上一上来就是个公式推导...让我很尴尬...

对于4N我的总结:

1. 当产生两层叶子节点数时, 我们就需要开4N的空间
2. 当产生一层叶子节点数时, 我们开2N的空间

也就是说最优的情况下开2N即可, 最差的情况下开4N, 那什么是最优和最差呢? [参考图1-3和图1-4]。
但是由于基本不能确定有多少元素, 所以最终就会开4N以空间换时间。
当然了, 以上仅仅是我个人的一个理解, 不一定是对的。望指教。

线段树实现

线段树数组表示

public class SegmentTree<E> {

    private E[] data ; // 线段树数据副本
    private E[] tree; // 使用数组实现线段树

    public SegmentTree(E[] arr) {
        this.data = (E[]) new Object[arr.length];
        for (int i = 0; i < arr.length; i++)
            this.data[i] = arr[i];

        // 开辟空间4倍, 形成满二叉树。空间换时间.
        this.tree = (E[]) new Object[arr.length * 4];
    }

    public E get(int index) {
        if (index < 0 || index >= data.length)
            throw new IllegalArgumentException("请输入正确的索引");
        return this.data[index];
    }

    public int getSize() {
        return data.length;
    }

    // 返回完全二叉树的数组表示左孩子的索引位置
    public int leftChild(int index) {
        return index * 2 + 1;
    }

    // 返回完全二叉树的数组表示右孩子的索引位置
    public int rightChild(int index) {
        return index * 2 + 2;
    }
}

将数组转换线段树

上面我们也说了, 线段树可以做区间的汇总, 查询, 最大最小。那么在构建线段树的时候, 线段树的节点存储的是什么? 叶子节点又存储的是什么?

1. 叶子节点存储的是实际具体的数字值
2. 非叶子节点存储什么内容主要和我们的业务关联比如我们是累加, 那么非叶子节点存储的就是l...r的总和, 如果是最大值或最小值则是l...r中最大值或者最小值信息。

如何划分线段树的区间呢? 文章开头已经说了, 不过会存在一个小问题

mid = L + (R - L) / 2

之所以采用这种方法而非(l+r)/2主要是为了防止数太大, 进而出现整形溢出。

现在我们已经清楚的知道如何划分线段树区间, 以及通过线段树数组表示代码获取到其左右孩子信息。

接下来我们就看看如何通过递归的方式构建线段树把。

public interface Merger<E> {
    E merge(E a, E b) ;
}

利用该接口, 可以动态实现线段树最大|最小|聚合操作等。

private Merger<E> merger;

// ++ 这里只有新增出来的部分
public SegmentTree(E[] arr, Merger<E> merger) {
  this.merger = merger;
  // 将数组构建成线段树
  // 初始化从下标0开始, 区间从0到数组末尾
  buildSegmentTree(0, 0, this.data.length -1);
}

// treeIndex的位置创建区间[l...r]的值
private void buildSegmentTree(int treeIndex, int l, int r) {

  // 如果数组长度只有1的话, 直接赋值退出
  if (l == r) {
      this.tree[treeIndex] = this.data[l];
      return ;
  }

  int leftTreeIndex = leftChild(treeIndex);
  int rightTreeIndex = rightChild(treeIndex);

  // 如果还能继续划分则需要更新区间数据
  int mid = l + (r - l) / 2;

  // 左孩子
  buildSegmentTree(leftTreeIndex, l, mid);

  // 右孩子
  buildSegmentTree(rightTreeIndex, mid + 1, r);

  // 如果我们是区间累加就将左右孩子值相加存储即可
  // 然鹅直接累加是不行的, E是不知道滴。
  // 不过如果直接进行相加了, 那么我们想要做最大|最小或者其它操作岂不是没法用了吗?
  // 我们创建一个接口, 用来实现我们我们想要的操作。
  // this.tree[treeIndex] = this.tree[leftChildIndex] + this.tree[rightChildIndex];

  this.tree[treeIndex] = merger.merge(this.tree[leftTreeIndex], this.tree[rightTreeIndex]);
}


@Override
public String toString() {
    StringBuffer res = new StringBuffer();
    res.append('[');
    for (int i = 0; i < tree.length; i ++) {
        if (tree[i] != null)
            res.append(tree[i]);
        else
            res.append("null");

        if (i < tree.length - 1)
            res.append(", ");
    }

    res.append(']');
    return res.toString();
}

线段树查询

图[1-6]这个线段树图片中, 如果我们要查找[2, 5]这个区间的的信息。
如果我们的Merger实现的累加操作, 则就是查询[2, 5]这个区间的总和。

如何查找呢? 从什么位置上开始查找呢? 当然还是从我们的根节点上开始查找。

1. 根节点包含的是[0...7]这个区间相应的信息, [2, 5]显然是[0...7]区间的一个子集。相应的要向下从这个根节点的左右子树种查找。对于线段树来说每一个节点他的左右子树都是从中间分隔开的, 所以我们是知道这个分隔的位置的。所以对于根节点来说, 他的左孩子是[0...3]区间的内容, 右孩子是[4...7]区间的内容。

2. 对于[2, 5]这个区间, 它有一部分落在[0...3]区间中, 另外一部分落在[4...7]区间中。所以我们要到根节点左右两个节点查询。具体是在左节点中查询[2...3]这个子区间, 右节点查找[4...5]这个区间。可以看到我们将[2, 5]拆成了两部分[2...3]和[4...5]两个子区间。分别到根节点左右两个孩子中去查找。

3. 我们从[0...3]这个区间查询[2, 3]这个子区间。我们知道[0...3]这个区间左孩子是[0...1]区间右孩子是[2...3]的区间, 由于[0...1]这个区间和我们查找的区间没有任何关系, 所以我们继续在[0...3]的右孩子[2, 3]继续查找。同理, 在查询[4...7]这个节点中查找[4, 5]这个区间, 它的左孩子包含[4, 5]这个区间, 右孩子包含[6, 7]这个区间。所以相应的我们要查找的[4, 5]区间和[6, 7]完全没有重叠, 所以到[4...7]的左孩子查找相应的数据就可以了。

4. 当然, 在查找到[2, 3]这个结果和[4, 5]这个结果的值时, 我们并不需要遍历到叶子节点, 直接返回[2, 3]和[4, 5]的值。但是由于是两个不同节点返回来的, 我们还需要对返回的结果进行组合。返回[2, 5]这个区间所对应的的结果。

5. 可以看到我们并不需要从头到尾遍历我们要查询[2, 5]的元素。我们只需要从我们根节点向下去找相应的子区间。在把我们查找到的子区间综合起来。查找的时候是和我们树的高度相关。而和我们查询区间的长度是无关的。正因为如此, 我们线段树是logn级别的查找也是logn级别的。

public E query(int queryL, int queryR) {
  if (queryL < 0 || queryL >= data.length ||
          queryR < 0 || queryR >= data.length || queryL > queryR)
      throw new IllegalArgumentException("请正确输入区间值");

  return query(0, 0, data.length -1, queryL, queryR);
}

private E query(int treeIndex, int l, int r, int queryL, int queryR) {
  if (l == queryL && r == queryR)
      return tree[treeIndex];

  int mid = l + (r - l) / 2;
  int leftTreeIndex = leftChild(treeIndex);
  int rightTreeIndex = rightChild(treeIndex);

  // 要查找的区间在右子树中
  if (queryL >= mid + 1)
      return query(rightTreeIndex, mid + 1, r, queryL, queryR);
  else if (queryR <= mid) // 要查找的区间在左子树中
      return query(leftTreeIndex, l, mid, queryL, queryR);

  // 当要查询的区间, 在左右子树中
  E leftQueryResult = query(leftTreeIndex, l, mid, queryL, mid);
  E rightQueryResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
  return merger.merge(leftQueryResult, rightQueryResult);
}

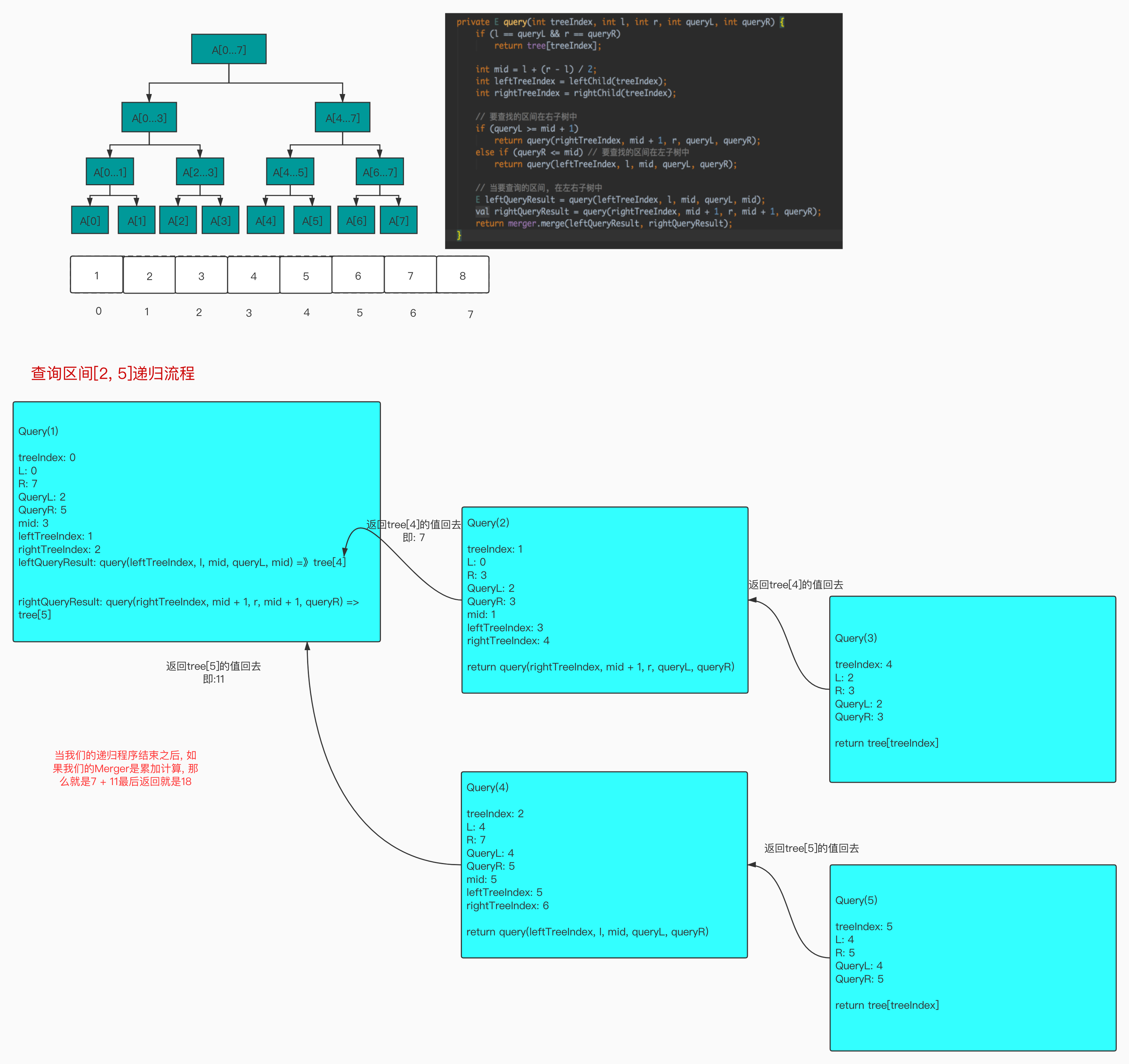
图[1-6]展示如何递归查找区间值。

[图1-6]

线段树更新

基本操作中, 我们已经学习区间查询, 但是区间如何更新呢? 更新需要注意哪些点呢?

线段树存储的是一个区间的值, 所以当我们更新叶子节点内容后, 还需要一级一级的往上推, 更新父节点的值。

所以, 更新操作分为两部分:

1. 查找到对应的索引并更新为新数据
2. 更新数据后, 依次更新父节点的值

public void set(int index, E e) {
    if (index < 0 || index >= data.length)
        throw new IllegalArgumentException("请正确输入索引位置.");

    data[index] = e;
    // 初始化从根节点开始, 查找到对应的叶子节点更新
    set(0, 0, data.length - 1, index, e);
}

private void set(int treeIndex, int l, int r, int index, E e) {
    if (l == r) {
        tree[treeIndex] = e;
        return ;
    }

    int mid = l + (r - l) / 2;
    int leftIndexTree = leftChild(treeIndex);
    int rightIndexTree = rightChild(treeIndex);

    // 如果索引位置大于中间值, 则一定在树的右侧, 否则在树的左侧。
    if (index >= mid + 1)
        set(rightIndexTree, mid + 1, r, index, e);
    else
        set(leftIndexTree, l, mid, index, e);

    // 最后不要忘记更新父节点的值
    tree[treeIndex] = merger.merge(tree[leftIndexTree], tree[rightIndexTree]);
}