Heap(堆)
Heap学前知识
堆的概念:
N个元素序列[k1, k2, k3, k4, k5, k6...kn]当且仅当满足以下关系时才会被称为堆。
当数据下标为1时: ki <= k2i, ki <= k2i+1 或者 ki >= k2i, ki >= k2i + 1
当数据下标为0时: ki <= k2i + 1, ki <= k2i + 2 或者 ki >= k2i + 1, ki >= k2i + 2
堆(heap)的实现通常是通过构造二叉堆, 因为应用较为普遍, 当不加限定时, 堆通常指的就是二叉堆。
二叉堆:
- 二叉堆是一棵完全二叉树(参考图1-1)
- 堆中的节点值总是不大于其父亲节点的值, 这种我们一般称为最大堆。反之亦然我们称为最小堆。(参考图1-2)
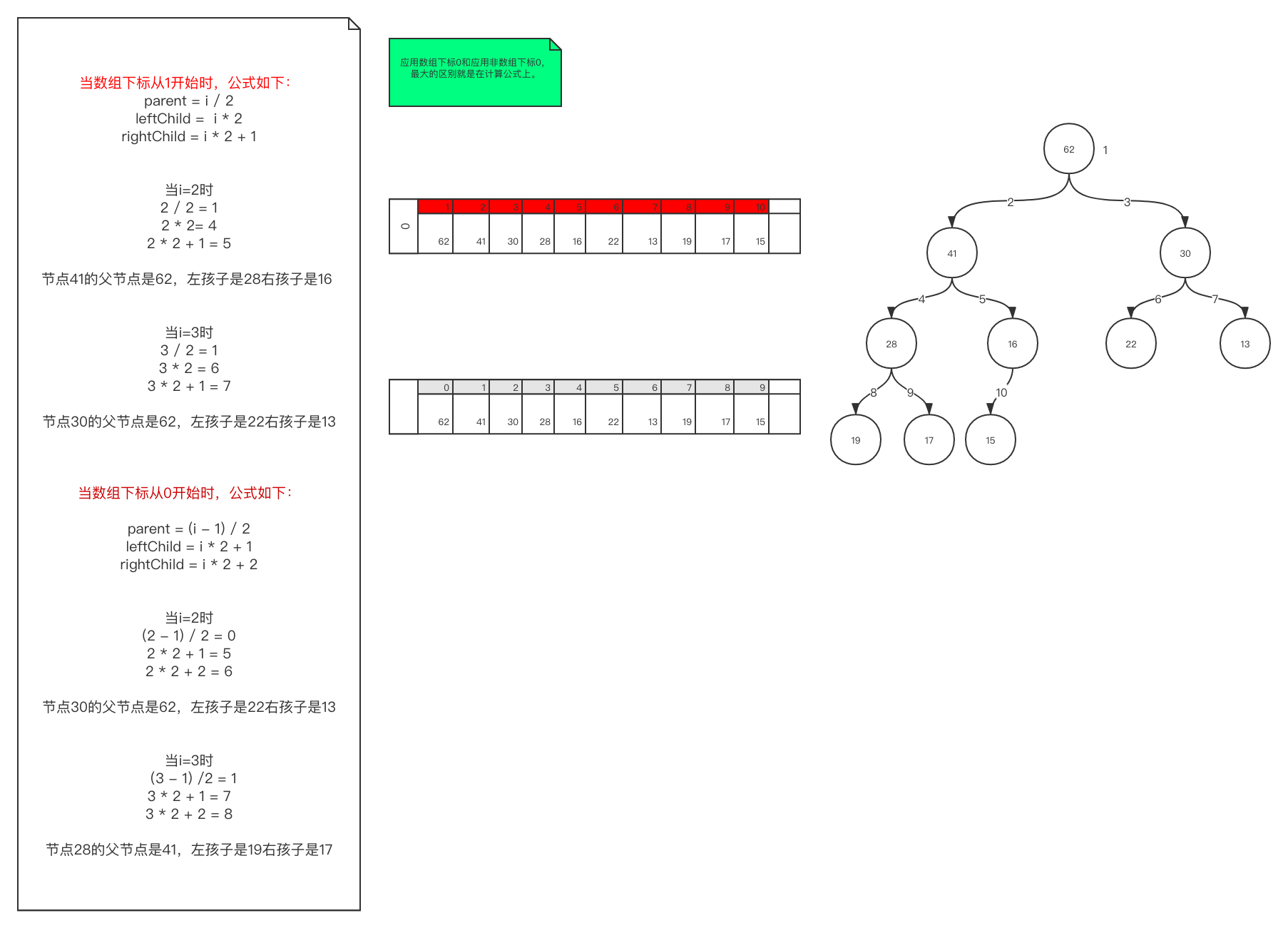
- 利用数组实现二叉堆(参考图1-3)
- 使用下标0的公式:
parent(i) = i / 2 left child (i) = 2 * i right child (i) = 2 * i + 1 - 使用下标1的公式:
parent(i) = (i - 1) / 2 left child (i) = 2 * i + 1 right child (i) = 2 * i + 2
- 使用下标0的公式:
图1-1
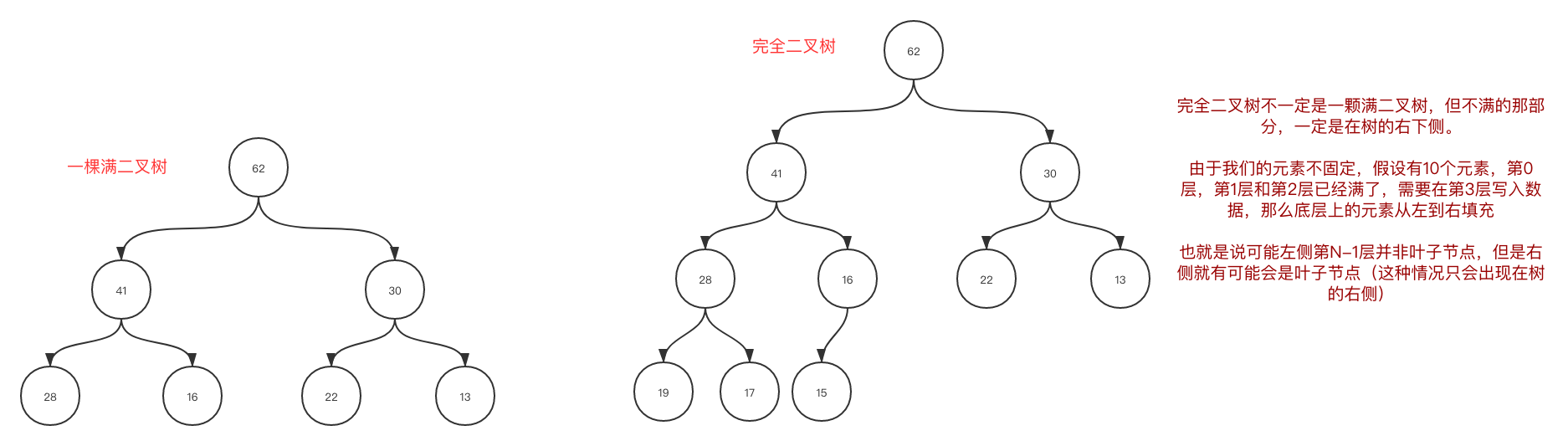
图1-2
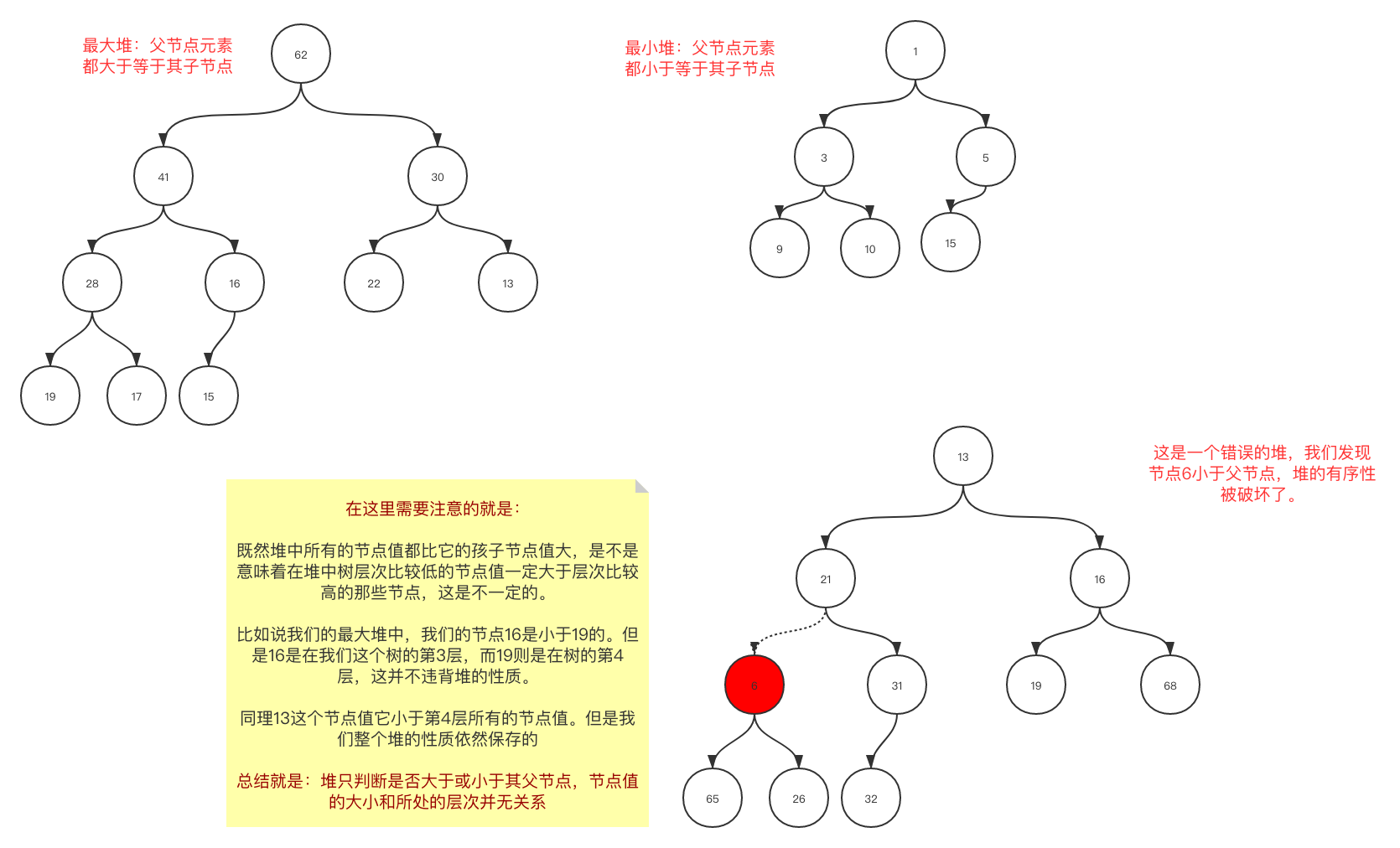
图1-3
最大堆的设计实现
初步结构
由于堆中的元素是需要进行比较的, 所以插入进来的元素都是需要带有可比较性的。这里我们继承Comparable即可。 这里我们用的是java自带的动态数组, 这样避免空间不充足问题。
为了方便查找元素的父节点以及左右孩子节点, 我们将其封装成方法, 这样无论是从数组下标0或者下标1开始对于我们来说 都是不关的, 我们只关心返回正确的节点索引位置数据。
public class MaxHeap<E extends Comparable<E>> {
private ArrayList<E> data;
public MaxHeap(int capacity) {
this.data = new ArrayList<>(capacity);
}
public MaxHeap() {
this.data = new ArrayList<>();
}
public int size() {
return data.size();
}
public boolean isEmpty() {
return data.size() == 0;
}
// 返回父元素在二叉堆中数组的索引位置
private int parent(int index) {
if (index == 0)
throw new IllegalArgumentException("该索引没有父节点");
return (index - 1) / 2 ;
}
// 返回左孩子索引
private int leftChild(int index) {
return index * 2 + 1;
}
// 返回孩子索引
private int rightChild(int index) {
return index * 2 + 2;
}
}
添加元素及上滤
现在我们需要向数组中添加元素, 但是添加进入的元素是否满足堆的特性呢? 如果不满足我们又要如何去处理呢?
当我们向数组中添加一个元素且不满足堆的特性时候, 我们需要进行一个上滤的过程(有些称为上浮), 用来达到并满足堆的特性。
如下图所示, 向数组中添加一个元素并且进行上滤的过程:
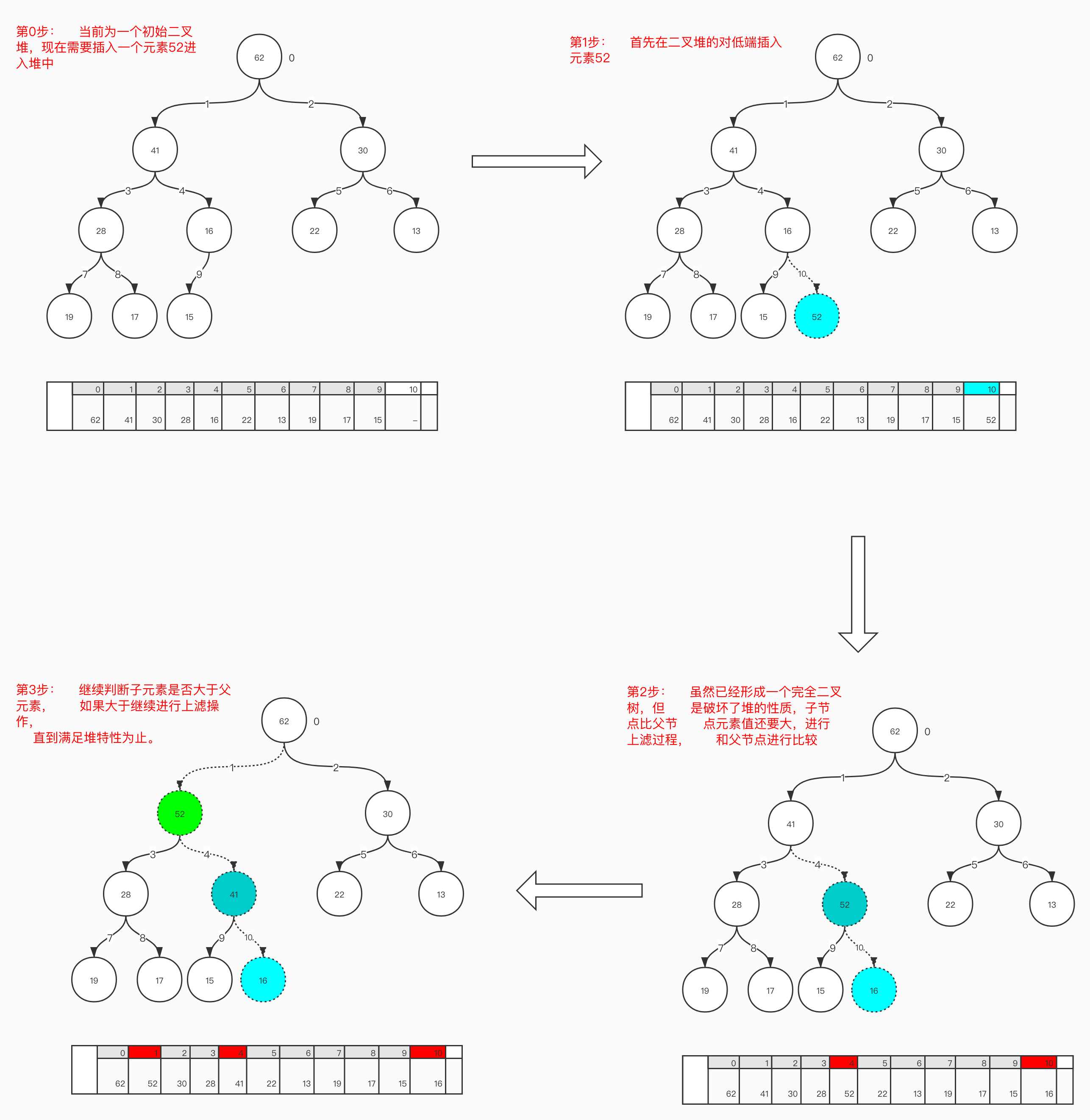
通过上面的图例过程, 我们清楚在插入的时候需要一直和自己父节点进行比较, 直到满足 堆的特性才算插入成功。
// 添加元素
public void add(E e) {
data.add(e);
// 将新加入的索引进行上滤, 添加是从最后添加的所以取最后元素索引位置
siftUp(data.size() - 1);
}
// 上滤过程
private void siftUp(int index) {
// 如果当前index为0表示为根节点, 根节点是没有父元素的所以没法比较, 并且父节点是小于子节点的
while (index > 0 && data.get(parent(index)).compareTo(data.get(index)) < 0) {
// 如果子节点大于父节点进行交换
swap(parent(index), index);
// 继续判断, 是否还大于祖先节点, 直到满足堆的特性
index = parent(index);
}
}
// 位置交换
private void swap(int p, int c) {
E t = data.get(p);
data.set(p, data.get(c));
data.set(c, t);
}
取出元素及下滤
由于堆是优先队列的结构, 所以只能从堆顶删除元素。移除堆顶元素之后, 用堆的最后一个节点填补取走的堆顶元素, 并将堆的实际元素个数减1。但用最后一个元素取代堆顶元素可能会破坏堆的特性, 因此需要将堆自顶向下进行调整(这个过程一般称为下浮或者下滤)使其满足最大堆或者最小堆。
下图是取出元素并进行下滤流程图:
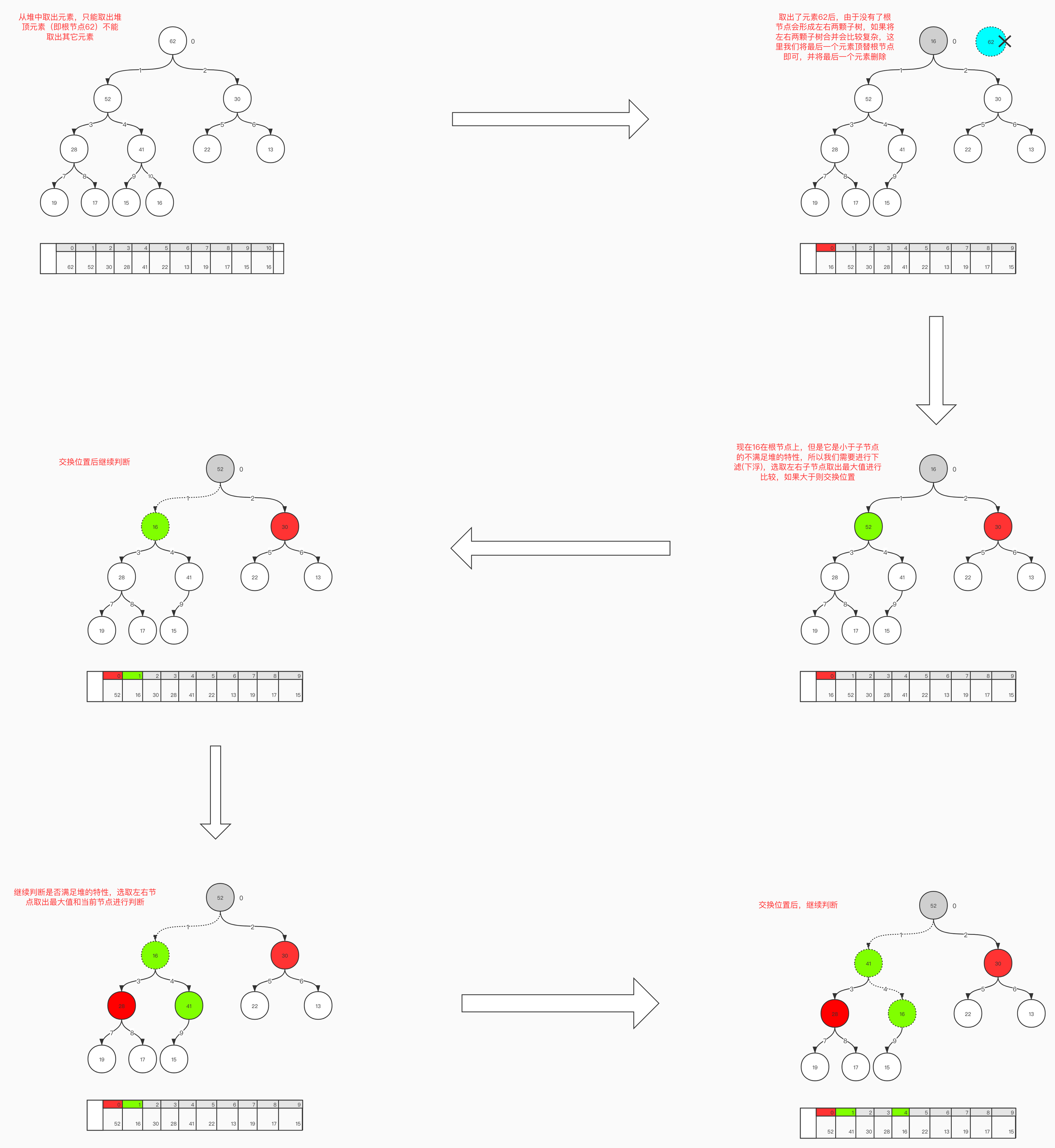
// 查找出最大元素
public E findMax() {
if (data.size() == 0)
throw new IllegalArgumentException("当前数组为空");
return data.get(0);
}
// 取出堆中最大元素
public E extractMax() {
// 1. 找到最大值
E ret = findMax();
// 2. 最后一个元素顶替最大值
swap(0, data.size() - 1);
// 3. 删除最后节点值
data.remove(data.size() - 1);
// 4. 下滤(下浮)过程
siftDown(0);
return ret ;
}
// 下滤节点
private void siftDown(int index) {
// 如果下滤到叶子节点, 在去获取当前索引位置左孩子肯定超出整个数组大小
while (leftChild(index) < data.size()) {
// 1. 获取到该索引的左右孩子
int k = leftChild(index);
// 需要判断是否存在右孩子
// k + 1的话相当左孩子索引位置+1得到了右孩子, 如果不大于数组长度则包含右孩子
if (k + 1 < data.size()) {
// 获取左右孩子中最大的元素节点
// 这里的判断是更新索引位置数据, 如果左孩子大于右孩子则不需要更新索引, 否则更新为右孩子的索引
if (data.get(k).compareTo(data.get(k + 1)) < 0) {
// k = rightChild(index);
++ k; // ++k 等价rightChild(k)
}
}
if (data.get(index).compareTo(data.get(k)) >= 0)
break;
// 进行交换数据
swap(index, k);
// 将下滤后的索引继续进行判断
index = k;
}
}
Replace和Heapify处理
-
Replace 定义: 取出堆中最大的元素, 然后放入一个新的元素。
实现原理:
- 可以直接将堆顶元素替换成新的元素, 然后进行下滤(下沉)操作。
-
Heapify
定义: 将任意数组转换成堆。
实现原理:
从最后一个非叶子节点开始计算。如图1-4,我们这个棵完全二叉树有5个叶子节点。
相应的倒数第一个非叶子节点就是元素22所在的节点。我们从这个节点开始倒着从后向前进行下滤操作。
如何定位最后一个非叶子节点索引位置呢?
取出数组最后一个索引位置, 更具最后一个索引位置计算获取到父节点索引位置。
图1-4
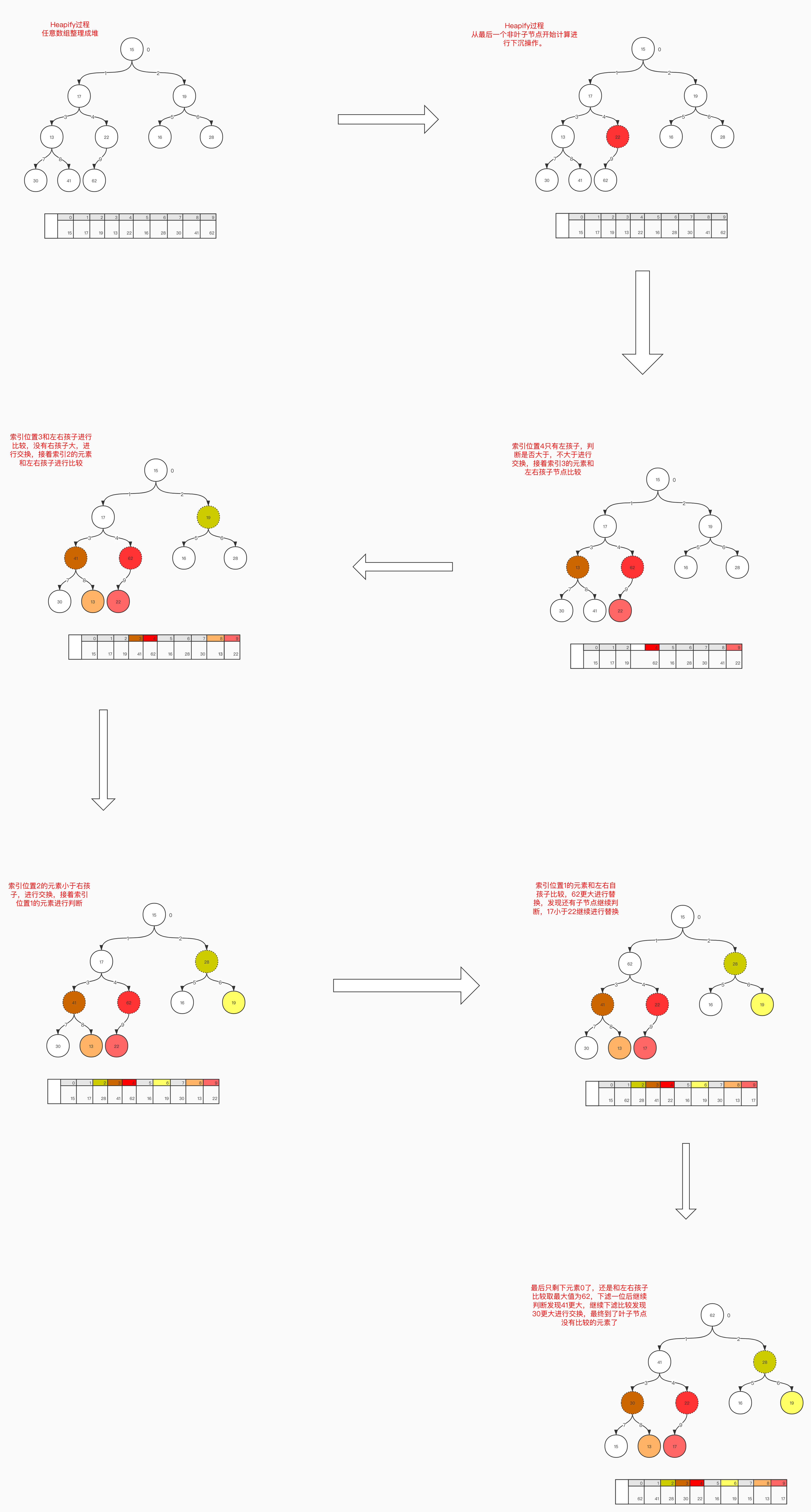
public E replace(E e) {
// 1. 找到最大元素
E ret = findMax();
// 2. 新插入的值替换堆顶元素
data.set(0, e);
// 3. 进行下沉操作
siftDown(0);
return ret;
}
/**
Heapify操作, 写成一个构造函数.
*/
public MaxHeap(ArrayList<E> data) {
this.data = data;
// 缩写, 直接获取到最后一个非叶子节点索引, 进行递减。
for (int i = parent(data.size() - 1); i >= 0; i--) {
siftDown(i);
}
// 1. 获取到最后一个非叶子节点的元素索引位置
// int p = parent(this.data.size() - 1);
// 2. 对p从后往前执行, 依次递减进行下沉操作
// while (p >= 0) {
// // 2. 进行下沉
// siftDown(p);
// p--;
// }
}
