数据结构-递归

小墨鱼3
471 阅读5分钟

链表与递归

简单介绍

前面我们已经介绍了链表, 然而这个主题主要是用于扩展学习链表的, 以及递归的基本使用。 链表练习主要以LeetCode为主, 然后给大家认识一下基础的递归使用以及调用流程等。

LeetCode链表问题

203. 移除链表元素

删除链表中等于给定值 val 的所有节点
示例:
输入: 1->2->6->3->4->5->6, val = 6 <>
输出: 1->2->3->4->5

然后, LeetCode给出的Node代码如下:

public class ListNode {
  int val;
  ListNode next;
  ListNode(int x) { val = x; }
}

使用非虚拟头结点解决方法:


public class Solution {
    public ListNode removeElements(ListNode head, int val) {

        // 删除头结点, 需要优先判断是否为空
        while (head != null && head.val == val) {
            head = head.next;
        }

        if (head == null) {
            return null; // 如果全部都是要删除的节点数据, 则中间数据不需要处理了
        }

        ListNode prev = head ;
        // 处理中间数据集
        while (prev.next != null) {
            if (prev.next.val == val) {
                prev.next = prev.next.next;
            } else {
                prev = prev.next;
            }
        }

        return head;
    }

    public static void main(String[] args) {
        Solution s = new Solution();
        ListNode node1 = new ListNode(3);
        ListNode node2 = new ListNode(3);
        ListNode node3 = new ListNode(3);
        ListNode node4 = new ListNode(3);

        node1.next = node2;
        node2.next = node3;
        node3.next = node4;

        s.removeElements(node1, 3);
    }
}

虚拟头结点版本

public ListNode removeElements(ListNode head, int val) {

        // 由于虚拟节点永远不会被访问到, 所以给个负数
        ListNode dummyHead = new ListNode(-1);
        dummyHead.next = head;


        // 应为有了虚拟头结点, 所以不需要关心头节点问题, 直接遍历
        ListNode prev = dummyHead ;
        // 处理中间数据集

        while (prev.next != null) {
            if (prev.next.val == val) {
                prev.next = prev.next.next;
            } else {
                prev = prev.next;
            }
        }

        // 虚拟节点是不会外暴露的, 需要需要next
        return dummyHead.next;
}

递归

递归简介

是指在函数的定义中使用函数自身的方法, 即自己调用自己。
本质上, 将原来的问题转换为更小的同一问题。

递归的优缺点

  • 优点

    • 大问题化为小问题,可以极大的减少代码量
    • 用有限的语句来定义对象的无限集合
    • 代码更简洁清晰，可读性更好

  • 缺点

    • 递归调用函数,浪费空间
    • 递归太深容易造成堆栈的溢出
参考:
  https://blog.csdn.net/acmman/article/details/80547512
  https://blog.csdn.net/laoyang360/article/details/7855860

第一个递归例子

现在我们有一组数组, 我们如何通过递归的形式进行累加并返回结果呢?

看看递归是如何调用的(后面还会详细介绍递归调用流程)

avatar


/**
  递归返回数组中的总和
*/
public class ArrayElementSum {

    public static int sum(int[] arr) {
        return sum(arr, 0) ;
    }

    private static int sum(int[] arr, int l) {
        if (l == arr.length)
            return 0; // 递归出口, 问题已经最小无法在分解了
        return arr[l] + sum(arr, ++ l); // 递归将问题更小化
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 4, 5, 6, 7, 8} ;
        System.out.println(sum(nums));
    }
}

递归函数执行流程

我们在学习栈的应用的时候, 就是程序调用的系统栈。在一个函数中调用一个子函数就会压入一个系统栈, 当子函数执行完之后就会从系统栈弹出 然后回到上次指定的地方并继续。

其实递归调用也就是这么一个过程, 只不过就是调用的还是这个函数本身而已。

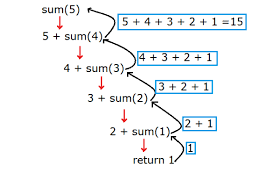
透过下图, 我们更加直观的了解上面的递归例子的执行流程把。

avatar

假设现在数组中只有数字[6, 10] 方便进行调试。数组长度为2。

sum函数执行过程为:

  1. 判断当前位置是否等于数组长度, 如果等于则返回, 否则往下执行
  2. 继续调用sum函数, 并传入对应的位置
  3. 当第一步成立后, 获取到函数返回值并加上当前位置数组的值。
  4. 返回累加后的结果

可能会迷糊的一些点:

  1. sum函数在调用sum函数的时候, 是新开辟的空间, 对应的参数参数值都是不同的,所以里面的变量是相互不会影响的。
  2. 千万不要被sum函数给迷惑了, 其本质上就是相当于A函数调用B函数, B函数调用C函数, 只不过现在是sum调用sum调用sum而已。我们可以编个号sum$0调用sum$1,sum$1调用sum$2, 然后sum$2的把结果返回给了sum$1, sum$1进行余下操作把结果sum$0, sum$0做完余下操作返回最终的结果值。这样是不是会好一点理解呢?



上面的例子可能会比较简单一点, 那下面我们来稍微复杂一点的, 比如删除链表的元素。

avatar

removeElements执行流程只有三步

  1. 判断当前头结点是否为null, 如果为null则返回
  2. 当前头结点的下一个节点为谁呢? 现在还不知道, 一直重复步骤1和2, 知道步骤1满足为止
  3. 如果当前头结点是要被删除的节点, 则返回的是他的下一个节点数据, 否则返回当前头结点数据

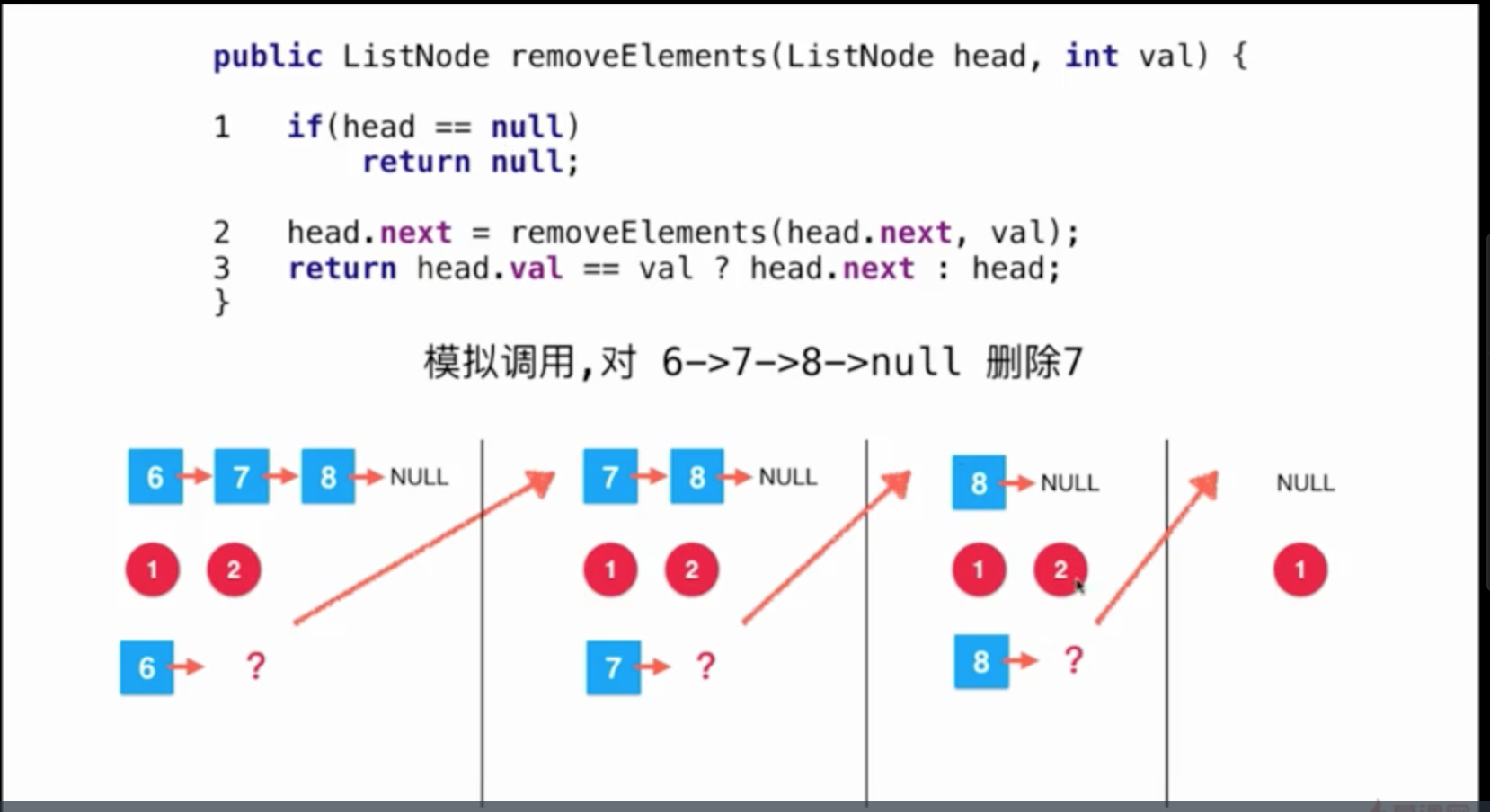
avatar

  1. 当我们以6为头结点执行第一步判断不为空则进入第二步"6"的下一个节点当前还不可知
  2. 当我们以7为头结点执行第一步判断不为空则进入第二步"7"的下一个节点当前还不可知
  3. 当我们以8为头结点执行第一步判断不为空则进入第二步"8"的下一个节点当前还不可知
  4. 当我们传入NULL后

下图

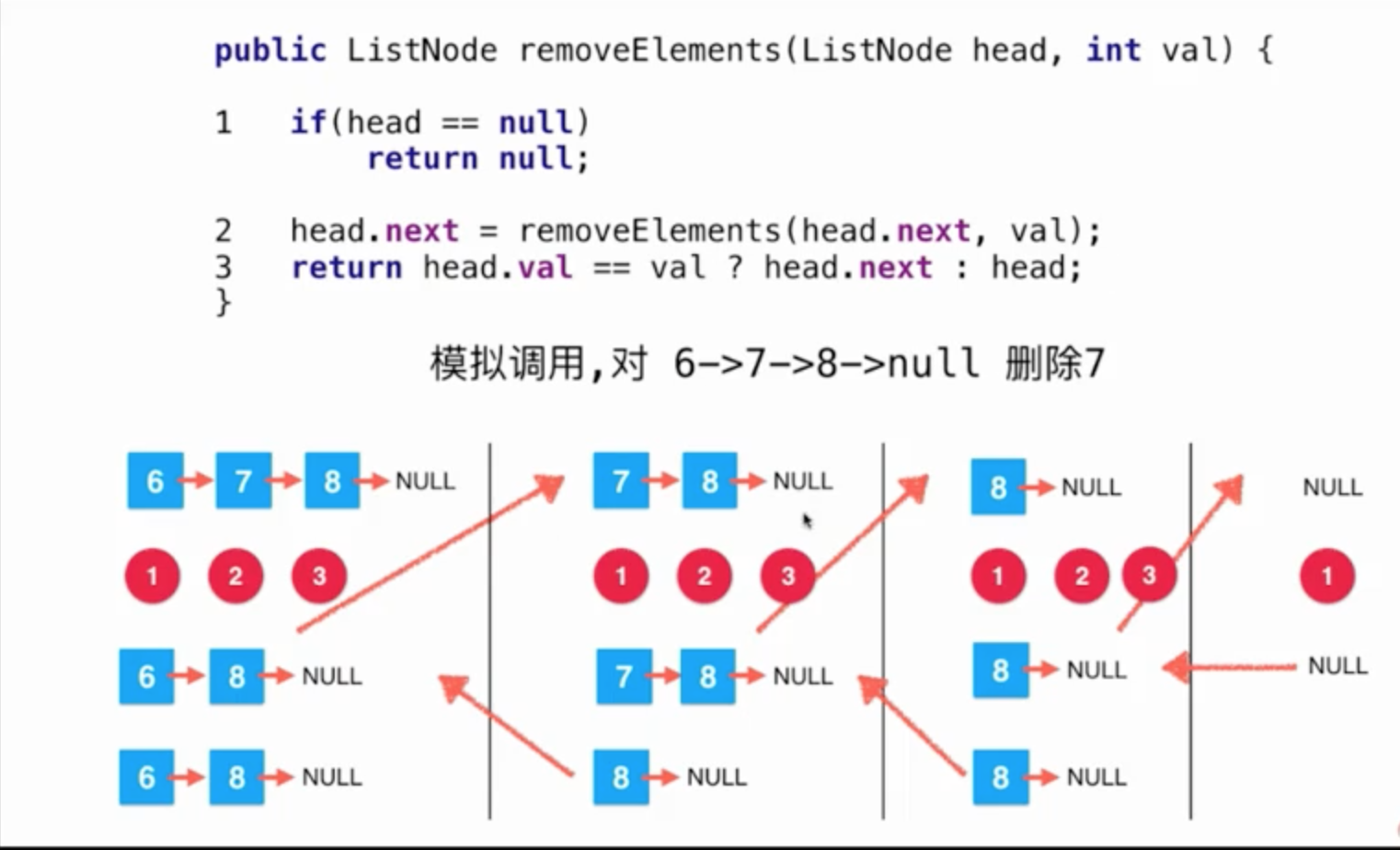
avatar

  1. 返回NULL值
  2. 头结点为8的next值为null, 判断当前头结点是否需要被删除, 当前节点不被删除返回 8 -> NULL
  3. 头结点为7的next值为8 -> NULL, 判断是否需要被删除, 需要删除则返回下一个节点即: 8 -> NULL
  4. 头结点为6的next值为8 -> NULL, 判断是否需要被删除, 不需要则返回 6 -> 8 -> NULL返回数据

到这里就已经结束了整个调用流程了。

avatar

avatar
文章
阅读
粉丝