数据结构-队列

队列

基本介绍

队列是一个先进先出(FIFO, First-In-First-Out)的线性表, 队列只允许在后端(rear)进行插入操作, 在前端(front)进行删除操作。

特点

• 先进先出

队列操作如下图所示

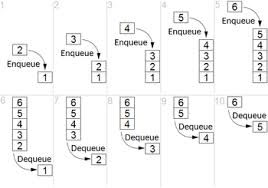
设计一个Queue

• 入队
• 出队
• 队首
• 队列长度
• 队列是否为空

public interface Queue<E> {
    // 入队
    void enqueue(E e);
    // 出队
    E dequeue();
    // 获取队首
    E getFront();
    int getSize();
    boolean isEmpty();
}

public class ArrayQueue<E> implements Queue<E> {

    private Array<E> array;

    public ArrayQueue(int capacity) {
        this.array = new Array<>(capacity);
    }

    public ArrayQueue() {
        this.array = new Array<>();
    }

    @Override
    public void enqueue(E e) {
        array.addLast(e);
    }

    @Override
    public E dequeue() {
        return array.removeFirst();
    }

    @Override
    public E getFront() {
        return array.getFirst();
    }

    @Override
    public int getSize() {
        return array.getSize();
    }

    @Override
    public boolean isEmpty() {
        return array.isEmpty();
    }

    @Override
    public String toString() {
        StringBuffer buff = new StringBuffer();
        buff.append("Queue: front [");
        for (int i = 0; i < array.getSize(); i ++) {
            buff.append(array.get(i));
            if (i < array.getSize() - 1)
                buff.append(",");
        }

        buff.append("] tail");
        return buff.toString();
    }
}

上面的代码底层是利用数组来实现的队列, 当我们进行出队的时候(即队首元素), 后面的所有元素都要向前移动一个单位。之后size--, 这是我们数组底层删除一个元素的操作。 由于所有元素都要向前移动一位这个操作在, 所以我们出队操作是O(n)。

假如现在我们不进行元素位置的移动, 记录一下当前的队首在哪。记录队尾的位置新元素添加的位置。

通过下图来看看循环队列

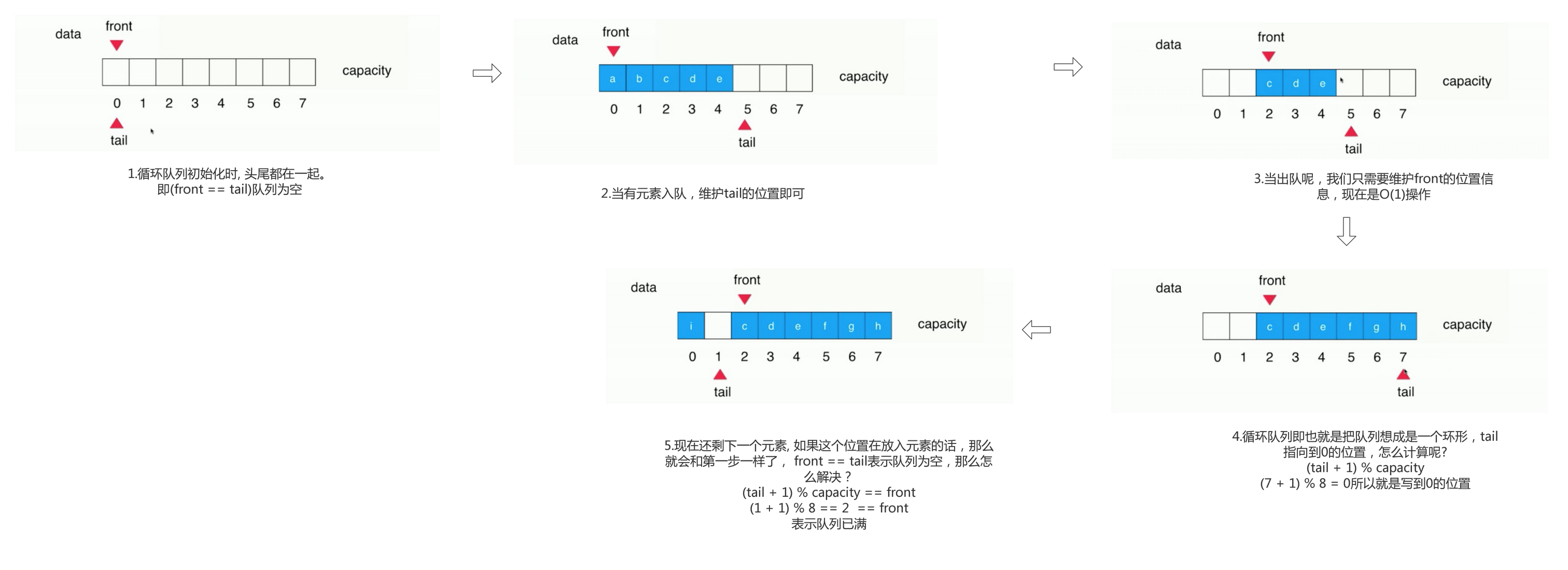
循环队列的设计

public class LoopQueue<E> implements Queue<E> {

    private E[] data;
    private int front, tail;
    private int size;

    public LoopQueue(int capacity) {
        // 在计算循环数组的时候, 我们需要浪费一个空间, 这样在计算tail + 1 == front的时候就可以用到或者说(tail + 1) % capacity == front
        data = (E[]) new Object[capacity + 1];
        front = 0;
        tail = 0;
        size = 0;
    }

    public LoopQueue() {
        this(10);
    }

    @Override
    public void enqueue(E e) {

        // 这里的取余计算使用的是data.length, 但是resize方法使用的是getCapacity()方法
        // 区别就是getCapacity里面长度-1, 毕竟我们多开了一个数组空间
        if ((tail + 1) % data.length == front) {
            resize(getCapacity() * 2) ;
        }

        data[tail] = e;
        tail = (tail + 1) % data.length;
        size ++;
    }

    private void resize(int newCapacity) {
        E[] newData = (E[]) new Object[newCapacity + 1];
        for (int i = 0 ; i < size; i ++) {
            newData[i] = data[(i + front) % data.length];
        }

        data = newData;
        front = 0;
        tail = size;
    }

    @Override
    public E dequeue() {

        if (isEmpty()) {
            throw new IllegalArgumentException("队列为空");
        }

        E ret = data[front];
        data[front] = null;
        front = (front + 1) % data.length;
        size --;
        if (size == getCapacity() / 4 && getCapacity() / 2 != 0)
            resize(getCapacity() / 2);

        return ret;
    }

    @Override
    public E getFront() {
        if (isEmpty()) {
            throw new IllegalArgumentException("队列为空");
        }
        return data[front];
    }

    @Override
    public int getSize() {
        return size;
    }

    @Override
    public boolean isEmpty() {
        return tail == front;
    }

    public int getCapacity() {
        return data.length - 1;
    }

    @Override
    public String toString() {
        StringBuffer buffer = new StringBuffer();
        buffer.append(String.format("Queue size = %d , capacity = %d\n", size, getCapacity()));
        buffer.append("front [");
        for (int i = front ; i != tail; i = (i + 1) % data.length) {
            buffer.append(data[i]);
            if ((i + 1) % data.length != tail) {
                buffer.append(", ");
            }
        }

        buffer.append("] tail");
        return buffer.toString();
    }
}