【原创·每日一题】通过一道例题快速掌握贪心算法

贪心算法是我们在日常开发中经常使用的一种算法，它的基本思想就是永远选择当前所有情况下最佳的情况。下面我们就通过一道例题来快速掌握一下贪心是如何来实际应用的。

题目描述

童年时候你和小伙伴在水泥地上玩游戏。你们在地上画了一个矩形网格，在每个格子中都有一个分数。你们约定：参加游戏的人只能从左往右从一个格子移动到下一列的另一个格子，每移动到下一列都可以任意换行一次。

现在你站在网格最左侧的任意一格开始游戏，并且可以在网格最右侧的任意一格结束游戏，然后和你的小伙伴比一比你们各自经过的所有格子的分数和谁最大。

请你设计一个程序来算一算你最多能得几分？

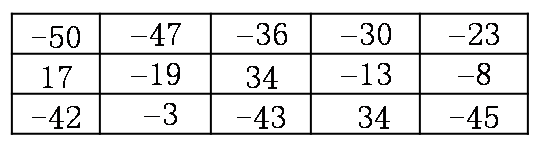
输入与输出要求

编写一个名为test的函数，调用它需要输入一个二维数组，其中每一个子数组储存了每一列中每格的分数。

最终函数输出求得的最大分数和。

测试样例

题目原理

由题意我们可以知道，因为你只能从左往右走，还要走到整个表格的最右边，且在此过程中每列你只能选取一个格子，因此如果想要获得最大分数，只需要每走到一列都选取分值最大的格子站即可，这便体现了贪心算法的思想，即每次都选取最佳情况。

代码实现

下面是JavaScript版本的题解：

function test(data) {
    let ans = [];
    let m = data[0].length;  //列总数
    let n = data.length;  //行总数
    //竖向遍历每行找出最大值
    for(let i = 0; i < m; i++) {
        let nums = [];
        for(let j = 0; j < n; j++) {  
            nums.push(data[j][i]);
        }
        ans.push(Math.max(...nums));
    }
    console.log(ans.reduce((x, y) => x + y));
}

后续

通过代码可以发现，贪心算法本身是非常简单的，但是它也有着非常大的局限性，即它只能确保找出当前情况下的最优解，但不一定是整个问题的最优解。

比如我们可以把这道题改一下，如果参与游戏者的起始位置和结束位置都是不确定的，贪心显然就不奏效了。那么这道题又该怎么办呢？下一篇文章我们接着谈。