参见 Stanford CS230学习笔记（二）：Lecture 2 Basics, Logistic Regression and Vectorizing

逻辑斯蒂回归

公式

$\hat{Y}=\sigma (w^TX+b)$

其公式中的各项数据含义如下：

• 输入X：假设输入为一张64*64的图片，那么依次取出R、G、B矩阵中的所有像素值，我们可以得到一个64*64*3的向量，将其记作x，即为一个输入；将样本集中每个样本的x(i)按列排成(64*64*3)*m的矩阵，记作X
• 输出Yhat：Yhat是一个1*m的矩阵，每个值代表相应的x的输出，其中的hat代表预测值
• 参数w b：需要利用梯度下降等方法寻找的参数，以使后续的代价函数最小化
• σ：sigmoid函数，用以归一化，将括号中的值限定在(0,1)范围内，$\sigma(z)=\frac{1}{1+e^{-z}}$

损失函数与代价函数

在逻辑斯蒂回归中，损失函数(Lost function)为 $L(\hat{y},y)=-(y\ln{(\hat{y})+(1-y)\ln(1-\hat y)})$

代价函数(Cost function)为 $J(w,b)=\frac{1}{m}\sum_{i=1}^m L(\hat y^{(i)},y^{(i)})$

推导

损失函数

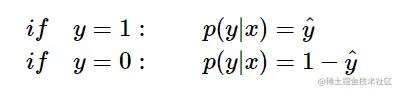
逻辑斯蒂回归概率的基本公式为 \begin{align} &if\quad y=1:\qquad p(y|x)=\hat y\\ &if\quad y=0:\qquad p(y|x)=1-\hat y \end{align}

合并起来

$p(y|x)=\hat{y}^y\cdot (1-\hat y)^{(1-y)}$

取自然对数（这里直接记作$\log$），以保证函数单增

$\log p(y|x)=y\log \hat{y} + {(1- y)} \log (1-\hat y)$ 为了最大化概率（的对数），我们需要最小化损失函数，因此两者增减性相反，添加负号即可 $L(\hat{y},y)=-(y\log{(\hat{y})+(1-y)\log(1-\hat y)})$ 该函数也称作交叉熵损失函数(Cross Entropy Loss)

代价函数

代价函数的公式是根据极大似然估计来的，就是数理统计里面那一套，样本先相乘再求对数，对数求导使导数等于0，得到极大似然估计值

至于为什么最后相乘变成了相加，是因为对数的存在，将连乘的对数变成了各项对数的连加

对于m个样本的整个训练集，服从独立同分布的样本的联合概率就是每个样本的概率的乘积

$\log \prod_{i=1}^{m}{p(y^{(i)}|x^{(i)})}=\sum_{i=1}^m \log {p(y^{(i)}|x^{(i)})}=-\sum_{i=1}^m L(\hat y^{(i)},y^{(i)})$

极大化似然概率就是极小化代价函数，因此增减性相反加负号，此处还要除上m

$J(w,b)=\frac{1}{m}\sum_{i=1}^m L(\hat y^{(i)},y^{(i)})$