矩阵分析 (二) 内积空间4）：当且仅当时成立。在线性空间中可以找到一组基底，这组基底本身线性无关，且其他元素可以被它

我的微信公众号名称：深度学习与先进智能决策 微信公众号ID：MultiAgent1024 公众号介绍：主要研究分享深度学习、机器博弈、强化学习等相关内容！期待您的关注，欢迎一起学习交流进步！

内积空间的基本概念

定义2.1：设 $V$ 是实数域 $P$ 上的线性空间，如果对于 $V$ 中任意两个元素 $\alpha$ ， $\beta$ 都有一个实数 $(\alpha, \beta)$ 与它们对应，并且满足下面的四个条件，则 $(\alpha,\beta)$ 称为元素 $\alpha$ , $\beta$ 的内积：

1）：对于任意的 $\alpha,\beta$ :

2）：对于任意的 $\alpha,\beta,\gamma$ :

(\alpha+\beta,\gamma) = (\alpha, \gamma)+(\beta, \gamma)

3）： $(k\alpha, \beta)=k(\alpha, \beta)$

4）： $(\alpha,\alpha) \geq 0$ 当且仅当 $\alpha=0$ 时成立。

正交基与子空间的正交

在线性空间中可以找到一组基底，这组基底本身线性无关，且其他元素可以被它线性表达，在内积空间中，可以有进一步的结果，即可以找到标准正交基。

定义2.2：由正交的单位向量 $\alpha_{1}，\alpha_{2}，\cdots，\alpha_{n}$ 组成的基底叫作标准正交基，这时：

\left(\boldsymbol{\alpha}_{i}, \boldsymbol{\alpha}_{j}\right)=\left\{\begin{array}{ll}{1,} & {i=j, \quad(i, j=1,2, \cdots, n)} \\ {0,} & {i \neq j}\end{array}\right.

可以说任意一个 $n$ 维欧氏空间中都存在标准正交基。

施密特(Schmidt)正交化的方法求标准正交基：

设 $\alpha_{1}，\alpha_{2}，\cdots , \alpha_{n}$ 是 $V$ 的一个基地。则 $\alpha_{1}，\alpha_{2}，\cdots , \alpha_{n}$ 线性无关。

首先取 $\beta_{1}=\alpha_{1}$ ，然后从第二项开始，把前面的向量的分量减去：

使 $\beta_{2}$ 与 $\beta_{1}$ 垂直，如下图(2.1)所示：

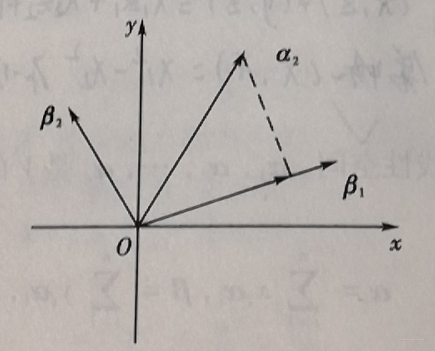
由：

(\alpha_{2}-k_{21}\beta_{1}，\beta_{1})=0

得：

k_{21}=\frac{(\alpha_{2},\beta_{1})}{(\beta_{1},\beta_{1})}

同样的设：

\beta_{3 }=\alpha_{3}-k_{31}\beta_{1}-k_{32}\beta_{2}

使 $\beta_{3}$ 与 $\beta_{1}$ ， $\beta_{2}$ 都垂直，即：

(\beta_{3},\beta_{1})=(\beta_{3},\beta_{2})=0

得：

k_{31}=\frac{(\alpha_{3},\beta_{1})}{(\beta_{1},\beta_{1})}，k_{32}=\frac{(\alpha_{3},\beta_{2})}{(\beta_{2},\beta_{2})}

由此做下去：

\beta_{n}=\alpha_{n}-k_{n1}\beta_{1}- \cdots - k_{n,n-1}\beta_{n-1}

k_{ni}=\frac{(\alpha_{n},\beta_{i})}{(\beta_{i},\beta_{i})},(i=1,2,\cdots,n-1)

最后把得到的向量 $\beta_{1}$ ， $\beta_{2}$ ， $\cdots$ ， $\beta_{n}$ 单位化，即得到标准正交基。

正交

前面讨论的过渡矩阵：

=(\alpha_{1}，\alpha_{2}，\cdots，\alpha_{n})A

这里 $A$ 一定是可逆的，如果 $\alpha_{1}，\alpha_{2}，\cdots，\alpha_{n}$ 和 $\beta_{1}，\beta_{2}，\cdots，\beta_{n}$ 都是标准正交基，可以有进一步的结果，即 $A$ 是正交的矩阵。

定义2.3：如果任取 $\alpha \in V_{1}$ ， $\beta \in V_{2}$ ， $(\alpha,\beta)=0$ ，则称 $V_{1}与V_{2}$ 正交。例如：

V_{1}=\{(x_{1},x_{2},0)| x_{1},x_{2} \in R\}

$V_{1}$ 与 $V_{2}$ 正交。

定义2.4：如果任取 $\beta \in V_{1}$ ， $(\alpha, \beta)=0$ ，则称 $\alpha$ 与 $V_{1}$ 正交。（这里也就是说 $\alpha$ 与空间 $V$ 中所有向量正交。）
定理2.1：如果子空间 $V_{1}$ 与 $V_{2}$ 是正交的，则它们的和 $V_{1}+V_{2}$ 是直和。

正交补

定义2.5：如果 $V$ 中子空间 $V_{1}$ 与 $V_{2}$ 正交，并且：

则称 $V_{1}(V_{2})$ 是 $V_{2}(V_{1})$ 的正交补，记作：

定理2.2： $n$ 维欧氏空间的任一子空间 $V_{1}$ 都有唯一的正交补。

点到子空间的距离与最小二乘法

证明欧氏空间中的一个向量 $\alpha$ 到一个子空间 $W$ 中的各个向量的距离也以垂线为最短：设 $\beta \in W$ 而 $\alpha-\beta$ 不垂直于 $W$ ， $\alpha-\gamma \perp W$ ， $\gamma \in W$ ，则：

|\alpha-\beta|^{2} = |\alpha-\gamma + \gamma -\beta|^{2} \\

=|\alpha-\gamma|^{2}+|\gamma - \beta|^{2}\\
\geq |\alpha-\gamma|^{2}

设 $W=L(\alpha_{1}，\cdots , \alpha_{s})$ ，而 $\alpha \in V$ ， $\alpha \perp W$ ，容易看出：

\alpha \perp W \Leftrightarrow \alpha \perp \alpha_{i} \quad(i=1,2, \cdots, s)

现在来看最小二乘法的问题：

解不相容的线性方程组 $AX=b$ ，这里 $R(A) \neq R(A,b)$ ，即方程组无解。现在找一个最小二乘解，也就是找一个近似程度最好的解。

设 $A=(\alpha_{1},\cdots,\alpha_{n})$ ,这里 $\alpha_{1},\cdots ,\alpha_{n}$ 是列向量，则：

A X=\left(\alpha_{1}, \cdots, \alpha_{n}\right)\left(\begin{array}{c}{x_{1}} \\ {\vdots} \\ {x_{n}}\end{array}\right)=\sum_{i=1}^{n} x_{i} \alpha_{i}

当 $X$ 的分量取遍所有值的时候，上面的表达式是：

的任意组合，所以：

而方程组无解意味着不存在一组 $x_{1}，\cdots , x_{n}$ 使 $AX=b$ ，即 $b$ 不能被 $\alpha_{1},\cdots,\alpha_{n}$ 组合出来， $b \notin W$ 。现在在 $L(\alpha_{1}，\cdots，\alpha_{n})$ 中找一个离 $b$ 最近的向量，即找一个 $\sum x_{i}\alpha_{i}=\beta$ ，使：

而 $b-\beta \perp W$ 时这个距离最小，当 $b-\beta \perp W$ 时，

b-\beta \perp \alpha_{i} (i=1,2,\cdots ,n)

这里 $b=\beta$ 与 $\alpha_{i}$ 都是列向量。所以：

即 $\alpha_{i}^{T}(b-\beta)=0$ ，写在一起得：

\left(\begin{array}{c}{\boldsymbol{\alpha}_{1}^{\mathrm{T}}} \\ {\boldsymbol{\alpha}_{2}^{\mathrm{T}}} \\ {\vdots} \\ {\boldsymbol{\alpha}_{n}^{\mathrm{T}}}\end{array}\right)(\boldsymbol{b}-\boldsymbol{\beta})=0,
\left(\begin{array}{c}{\boldsymbol{\alpha}_{1}^{\mathrm{T}}} \\ {\boldsymbol{\alpha}_{2}^{\mathrm{T}}} \\ {\vdots} \\ {\boldsymbol{\alpha}_{n}^{\mathrm{T}}}\end{array}\right)=A^{\mathrm{T}},
\beta=AX

所以最小二乘解是：

正规矩阵

如果把数域扩大到复数，则可以仿照实数空间内积的定义，把内积推广到复数，但是要考虑到复数的特性。

定义2.6：设 $V$ 是复数域 $C$ 上的线性空间，如果对 $V$ 中的任意向量 $\alpha,\beta$ ，都有一个复数 $\alpha,\beta$ 与之对应，且满足如下条件，则 $(\alpha,\beta)$ 称为 $V$ 的内积。

$(\alpha,\beta)=(\beta,\alpha)$
$(\alpha+\beta，\gamma)=(\alpha,\gamma)+(\beta,\gamma)$
$(k\alpha,\beta)=k(\alpha,\beta)$
$(\alpha,\alpha) \geq 0$ ，当且仅当 $\alpha=0$ 时 $(\alpha,\alpha)=0$

这时 $V$ 称为复内积空间或者酉空间，这里 $(\beta,\alpha)$ 是 $\beta,\alpha$ 的共轭，条件4）是保证 $\alpha,\alpha$ 是实数，否则可能会有 $\alpha \neq 0$ ，但是 $(\alpha \cdot \alpha)=0$ ,如 $\alpha=(3,4,5i)$

定义2.7：设 $A \in C^{n \times n}$ 且 $A^{H}A=AA^{H}=E$ ，则称 $A$ 为酉矩阵。这是实数空间正交矩阵的推广。
酉矩阵具有以下性质： 1） $|A|=1$ ； 2） $A^{-1}=A^{H}$ , $(A^{-1})^{H}=(A^{H})^{-1}$ ； 3） $A^{-1}$ 也是酉矩阵，两个酉矩阵的乘积也是酉矩阵； 4） $A$ 的行(列)向量构成标准正交基。
定义2.8：设 $A \in C^{n \times n}$ ,且 $A^{H}A=AA^{H}$ ,则 $A$ 称为正规矩阵。