BP神经网络（三）

一、BP神经网络

  本程序较为完整，帮助回顾一遍网络的整个运算过程。另外，本程序能够增加网络层数，并自由设定隐层神经元个数。

  首先定义类error BackPropagation neural network

class BPNN:

  构造函数用来定义整个网络结构，默认网络结构为[2,4,1]，包含一个输入层、一个隐层，一个输出层，输入层包含2个神经元，隐层包含4个神经元，输出层包含1个神经元。实际应用中，可以手动输入网络结构，如定义bp=BPNN([64, 128, 64, 10])，即修改成了对应的网络结构。这种对应关系实际上是通过矩阵运算来完成的。如[64, 128]，两层网络之间形成一个权值矩阵，该矩阵的大小是64*128，对输入层输入1*64的矩阵，两矩阵相乘后得到1*128的矩阵，经激活函数后作为下一层的输入值。其他值原理类似。

def __init__(self, nn_shape=[2, 4, 1]):
    self.W = []  # 权重
    self.B = []  # 阈值
    self.O = []  # 各神经元节点输出
    self.grads = []  # bp算法中误差与神经节点输入的微分(梯度项)

    self.mean = np.zeros(nn_shape[2]) #平均值用于数据预处理
    self.mean = self.mean.reshape((1, nn_shape[2]))

    self.W_shape = []  # 存储各矩阵的shape
    self.B_shape = []
    self.O_shape = []
    self.grads_shape = []

    self.errs = []  # 记录每次迭代的误差

    for index in range(len(nn_shape) - 1):  # 初始化W,B,O,grads矩阵
        self.W.append(2 * np.random.random([nn_shape[index], nn_shape[index + 1]]) - 1)
        self.W[index] = self.W[index].reshape([nn_shape[index], nn_shape[index + 1]])
        self.W_shape.append(self.W[index].shape)

        self.B.append(2 * np.random.random(nn_shape[index + 1]) - 1)
        self.B[index] = self.B[index].reshape(1, nn_shape[index + 1])
        self.B_shape.append(self.B[index].shape)

        self.O.append(np.zeros(nn_shape[index + 1]))
        self.O[index] = self.O[index].reshape(1, nn_shape[index + 1])
        self.O_shape.append(self.O[index].shape)

        self.grads.append(np.zeros(nn_shape[index + 1]))
        self.grads[index] = self.grads[index].reshape(1, nn_shape[index + 1])
        self.grads_shape.append(self.grads[index].shape)

        self.y_hat = self.O[-1]
        self.y_hat = self.y_hat.reshape(self.O[-1].shape)

        print('建立{}层神经网络网络'.format(len(nn_shape)))
        print(self.W_shape)
        print(self.B_shape)
        print(self.O_shape)
        print(self.grads_shape)

  sigmoid函数

def sigmoid(self, x):
    '''
    x为1*n向量
    '''
    return 1.0 / (1.0 + np.exp(-x))

  sigmoid函数的导数

def sigmoid_derivate(self, x):
    '''
    x为1*n向量
    '''
    return x * (1 - x)

  在处理多分类问题时，除使用sigmoid函数作为激活函数外，隐层与输出层间常使用softmax函数来计算网络的最终输出，并用交叉熵来计算网络误差。这往往比使用sigmoid函数和均方误差来训练网络的性能更优异。

  softmax激活函数：

其中为个输入，对应个输出神经元，公式中计算的是第个神经元的输出，可以看作是概率输出。

def softmax(self, x):
    '''
    x为1*n向量
    '''
    exp_all = np.exp(x)
    return exp_all / np.sum(exp_all)

  交叉熵：

代表第个神经元的期望输出，代表第个神经元的实际输出。

  BP神经网络在处理多分类问题时通常会将期望标签转化为one-hot编码的形式，例如一个三分类问题的标签分别为[1,0,0], [0,1,0], [0,0,1]

def one_hot_label(self, Y):
    '''
    将label转化为0001形式，若label有3种，则转化为100,010,001
    这里的label必须从0开始
    '''
    category = list(set(Y[:, 0]))
    Y_ = np.zeros([Y.shape[0], len(category)])

    for index in range(Y.shape[0]):
        Y_[index, Y[index, 0]] = 1

        return Y_

  使用one-hot编码后，交叉熵只有期望输出为1的神经元不为0。

  所以交叉熵的公式可转化为：

代表期望输出为1的神经元的实际输出。

#交叉熵
def cross_entropy(self, y, y_hat):
    tmp = np.argwhere(y == 1)
    return -np.log(y_hat[0, tmp[0, 1]])

  根据交叉熵可以推导出输出层梯度的计算公式，当前神经元为期望输出为1时：

  当前神经元期望输出不是1时：

  以上推导公式将会在信号向前传播的代码中体现。

  均方误差：

def error(self, y, y_hat):
    err = y - y_hat
    return 0.5 * err.dot(err.T)

  数据预处理

#数据预处理(标准化，使其满足标准正态分布)
def preprocess(self, X):
    self.mean = np.mean(X, axis=0)
    self.var = X.var()
    X = (X - self.mean) / self.var

  以下进入BP神经网络的迭代过程。迭代方式依据公式写出。

  1.信号向前传播

def update_output(self, x):

    '''更新各神经元的输出值，x为n*1向量'''

    for index in range(len(self.O)):
        if index == 0:
            self.O[index] = self.sigmoid(
                x.dot(self.W[index]) + self.B[index])
        elif index == len(self.O) - 1:
            self.O[index] = self.softmax(
                self.O[index - 1].dot(self.W[index]) + self.B[index])
        else:
            self.O[index] = self.sigmoid(
                self.O[index - 1].dot(self.W[index]) + self.B[index])

        self.O[index] = self.O[index].reshape(self.O_shape[index])

    self.y_hat = self.O[-1]
    self.y_hat = self.y_hat.reshape(self.O[-1].shape)
    return self.y_hat

  2.反向计算网络梯度

def update_grads(self, y):
    '''
    更新梯度值，y为p*1向量
    '''
    for index in range(len(self.grads) - 1, -1, -1):
        if index == len(self.grads) - 1:
            '''#该代码用来计算使用均方误差和sigmoid函数的二分类问题
            self.grads[index] = self.sigmoid_derivate(
                self.O[index]) * (y - self.O[index])
            '''
            tmp = np.argwhere(y == 1)

            for index_g in range(self.grads[index].shape[1]):
                if index_g == tmp[0, 1]:
                    self.grads[index][0, index_g] = 1 - self.O[index][0, index_g]
                else:
                    self.grads[index][0, index_g] = - self.O[index][0, index_g]
        else:  # 链式法则计算隐含层梯度
            self.grads[index] = self.sigmoid_derivate(
                self.O[index]) * self.W[index + 1].dot(self.grads[index + 1].T).T

        self.grads[index] = self.grads[index].reshape(
            self.grads_shape[index])

  3.更新权值和阈值

def update_WB(self, x, learning_rate):
    for index in range(len(self.W)):
        if index == 0:

            self.W[index] += learning_rate * x.T.dot(self.grads[index])
            self.B[index] -= learning_rate * self.grads[index]
        else:
            self.W[index] += learning_rate * self.O[index - 1].T.dot(self.grads[index])
            self.B[index] -= learning_rate * self.grads[index]
        self.B[index] = self.B[index].reshape(self.B_shape[index])

  训练函数

#训练
def fit(self, X, Y, Preprocess=True, thre=0.03, learning_rate=0.001, max_iter=100):
    '''
    将样本和label输入，X,Y中的样本均为行向量
    '''
    if Preprocess == True:
        X = self.preprocess(X, method=method)

    err = np.inf
    count = 0

    while err > thre:
        err = 0
        for index in range(X.shape[0]):

            x = X[index, :].reshape((1, -1))
            y = Y[index, :].reshape((1, -1))

            self.update_output(x)
            x = X[index, :].reshape((1, -1))
            self.update_grads(y)
            self.update_WB(x, learning_rate=learning_rate)
            err += self.cross_entropy(y, self.y_hat)
        err /= index + 1
        self.errs.append(err)
        count += 1
        if count > max_iter:
            print("超过最大迭代次数{}".format(max_iter))
            break

        print(count)
        print(err)

二、手写数字识别

  将第一部分程序的代码写入py文件中，命名为BP_neural_network。再建立一个文件，使用import即可导入写好的类。

import BP_neural_network as BP
from sklearn.datasets import load_digits #手写数字识别数据集

  手写数字识别选用sklearn中的数据集

from sklearn.datasets import load_digits #手写数字识别数据集

  手写数字识别数据集包含64个属性，一个分类标识，包含0~9共计10个数字。因此设定输入层神经元数为64，输出层神经元数为10。隐层神经元数可自由设定，但针对不太复杂的数据集建议不要设定太多神经元数，以免过拟合。

bp = BP.BPNN([64, 128, 64, 10])#建立神经网络对象
Y = bp.one_hot_label(Y) #one-hot编码

  建立网络结构

  根据输入参数，建立的网络结构如上图，包含1个输入层、1个输出层，2个隐层。下面是所需矩阵的大小，第一层是权值矩阵，第二层是阈值矩阵，第三层是输出值矩阵，第四层是梯度矩阵。

  训练网络

bp.fit(train_data, train_label, Preprocess=True,thre=0.01, learning_rate=0.005, max_iter=1000)#训练网络

  误差曲线

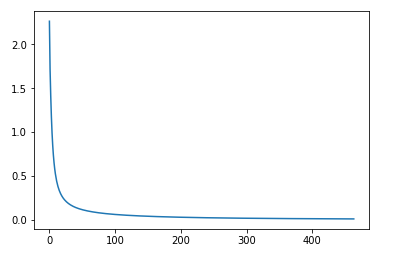
  由图可看出，训练到100次左右时误差不再明显变化。

  整个训练用时139秒，准确率达到93.2%

  可见训练时间较长，但准确率较高。

三、使用sklearn库函数构建网络

  选取多层感知机

#多层感知机
from sklearn.neural_network import MLPClassifier

  设置计算方式为随机梯度下降（sgd），其它参数与第二部分相同。

mlp = MLPClassifier(solver='sgd',hidden_layer_sizes=[128,64],max_iter=1000,learning_rate_init=0.005,verbose=True)

  数据集仍采用手写数字识别

mlp.fit(train_data, train_label) #训练

  训练用时1.73秒，准确率为92%

  使用同样数据集，对比第二部分，sklearn的多层感知机函数所需时间极短，准确率与第二部分相似。