动态规划(Dynamic Propramming)
#伪代码
for k=1,2,... do
for 所有状态s in S do
使用迭代式更新值函数v
end for
end for
策略提升
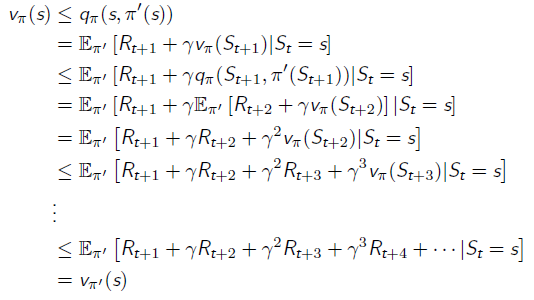 策略迭代
策略迭代
#伪代码
随机初始化V(s)和pi(s)
repeat
对于当前策略pi,使用迭代式策略评价的算法评估vpi,
使用贪婪策略提升得到vpi'
until 策略保持不变
策略评价不一定要收敛到vπvπ才能进行策略提升,可以提前引入停止的规则:
如值函数更新的差值足够小则停止;限定迭代次数等
广义策略迭代(Generalised Policy Iteration,GPI)不限定两者的方法:
策略评价:估计vπvπ,任何策略评价方法均可;
策略提升:提升策略π′≥ππ′≥π,任何策略提升算法均可
值迭代
任何最优的策略都能被分解成两部分:
最优的初始动作A
从后继状态开始沿着最优策略继续进行
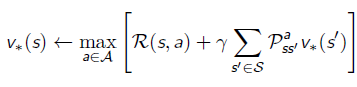
问题仍然是找到最优的策略,但在更新过程中并没有显式的策略值迭代 vs 策略迭代[td]
[td]
实时动态规划
全宽备份和样本备份
当一个精确的环境模型时,可以用动态规划去解决。总体来说,就是将一个问题分解成子问题,通过解决子问题来解决原问题。动态指针对序列问题,规划指优化,找到策略。
动态规划解决的问题具备两种性质:
动态规划解决的问题具备两种性质:
- 最优子结构
- 满足最优性原理
- 最优的解可以被分解成子问题的最优解
- 交叠式子问题
- 子问题能够被多次重复
- 子问题的解要能够被缓存并再利用
MDPs满足以上两个特性:
- 贝尔曼方程用递归的形式,把问题分解成子问题
- 值函数有效的存储了子问题的解,能够再利用
因此动态规划可以应用于MDPs的问题,使用动态规划解决强化学习问题时,要求指导MDPs的所有元素:
- 贝尔曼方程用递归的形式,把问题分解成子问题
- 值函数有效的存储了子问题的解,能够再利用
因此动态规划可以应用于MDPs的问题,使用动态规划解决强化学习问题时,要求指导MDPs的所有元素:
- 评价
- 输入:MDP<S,A,P,R,γγ> 和策略ππ 或者 MRP<S,Pπ,Rπ,γPπ,Rπ,γ>
- 输出:值函数vπvπ
- 优化
- 输入: MDP<S,A,P,R,γγ>
- 输出:最优值函数v∗v∗ 和最优策略π∗π∗
问题:给定一个策略<span class="MathJax" id="MathJax-Element-1955-Frame" tabindex="0" data-mathml="π" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">ππ,求对应的值函数<span class="MathJax" id="MathJax-Element-1956-Frame" tabindex="0" data-mathml="vπ(s) or qπ(s,a)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">vπ(s) or qπ(s,a)vπ(s) or qπ(s,a)
解决方法:
解决方法:
- 直接解:<span class="MathJax" id="MathJax-Element-1957-Frame" tabindex="0" data-mathml="vπ=(1−γPπ)−1Rπ" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">vπ=(1−γPπ)−1Rπvπ=(1−γPπ)−1Rπ
- 可以直接求得精确解
- 时间复杂度比较高O(n3)O(n3)
- 迭代解:<span class="MathJax" id="MathJax-Element-1959-Frame" tabindex="0" data-mathml="v1−>v2−>...−>vπ" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">v1−>v2−>...−>vπv1−>v2−>...−>vπ
- 利用贝尔曼期望方程迭代求解,可以收敛到最优解
贝尔曼期望方程:vπ(s)=∑a∈Aπ(a|s)(R(s,a)+γ∑s′∈SPass′vπ(s′))vπ(s)=∑a∈Aπ(a|s)(R(s,a)+γ∑s′∈SPss′avπ(s′))
可以得到如下迭代等式:vk+1(s)=∑a∈Aπ(a|s)(R(s,a)+γ∑s′∈SPass′vk(s′))vk+1(s)=∑a∈Aπ(a|s)(R(s,a)+γ∑s′∈SPss′avk(s′))
简写为vk+1=Rπ+γPπvkvk+1=Rπ+γPπvk - 利用贝尔曼期望方程迭代求解,可以收敛到最优解
- 备份:
vk+1(s)vk+1(s)需要用到vk(s′)vk(s′),用vk(s′)vk(s′)更新vk+1(s′)vk+1(s′)的过程称为备份。更新状态s的值函数称为备份状态s- 同步:每次更新都需要更新完所有的状态
#伪代码
for k=1,2,... do
for 所有状态s in S do
使用迭代式更新值函数v
end for
end for
策略提升
策略性价值函数通过筛选方式来改进策略,有几个常见的策略筛选方式:
贪婪策略,e-greedy策略,高斯策略,玻尔兹曼策略
策略提升定理
对于两个确定的策略π′π′和ππ,如果满足qπ(s,π′(s))≥vπ(s)qπ(s,π′(s))≥vπ(s),那么我们可以得到
vπ′(s)≥vπ(s)vπ′(s)≥vπ(s)
迭代过程:
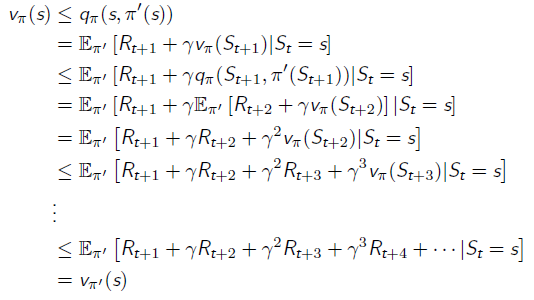
通过不断地交替运行策略评价和策略提升,使策略收敛到最优的策略的过程即为策略迭代

策略提升终止时,值函数达到最优,具体算法过程:
#伪代码
随机初始化V(s)和pi(s)
repeat
对于当前策略pi,使用迭代式策略评价的算法评估vpi,
使用贪婪策略提升得到vpi'
until 策略保持不变
策略评价不一定要收敛到vπvπ才能进行策略提升,可以提前引入停止的规则:
如值函数更新的差值足够小则停止;限定迭代次数等
广义策略迭代(Generalised Policy Iteration,GPI)不限定两者的方法:
策略评价:估计vπvπ,任何策略评价方法均可;
策略提升:提升策略π′≥ππ′≥π,任何策略提升算法均可
值迭代
任何最优的策略都能被分解成两部分:
最优的初始动作A
从后继状态开始沿着最优策略继续进行
最优性原理:
一个策略π(a|s)π(a|s)能够实现从s开始的最优值函数,vπ(s)=v∗(s)vπ(s)=v∗(s),当且仅当对于任何从状态s开始的后继状态s′s′,ππ能实现从状态s′s′开始的最优值函数vπ(s′)=v∗(s′)vπ(s′)=v∗(s′),由此可知只要知道v∗(s′)v∗(s′),即可以知道v∗(s)v∗(s),我们只需要选择一步动作即可
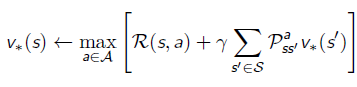
值迭代的两种理解:
- 策略迭代中,在策略评价阶段,只迭代一步,更新一下值函数而已
- 利用贝尔曼最优方程进行迭代
- 策略迭代中,在策略评价阶段,只迭代一步,更新一下值函数而已
- 利用贝尔曼最优方程进行迭代
问题仍然是找到最优的策略,但在更新过程中并没有显式的策略
同步备份下的值迭代算法:
#伪代码
for k=1,2,...do
for 所有的状态s in S do
通过公式更新v
end for
end for
值迭代 | 策略迭代 |
没有显式策略 | 有显式策略 |
迭代过程中的值函数可能不对应任何策略 | 迭代过程中的值函数对应了某个具体策略 |
效率较高 | 效率较低 |
贝尔曼最优方程 | 贝尔曼期望方程+贪婪策略提升 |
同步备份下的三种算法总结
问题 | 贝尔曼方程 | 算法 |
评价 | 贝尔曼期望方程 | 迭代式策略评价 |
优化 | 贝尔曼期望方程+贪婪策略提升 | 策略迭代 |
优化 | 贝尔曼最优方程 | 值迭代 |
上述算法都是基于状态值函数的(V函数)复杂度为O(mn2)O(mn2),可以拓展到状态动作值函数(Q函数)复杂度为O(m2n2)O(m2n2)
动态规划引申
异步动态规划
同步规划每次迭代都会同时保存所有状态的值函数,异步动态规划以某种顺序单独考虑每一个状态,能够大大减少计算量,只要所有的状态都能被持续的选择到,收敛性能够保证,常用的三种方式:
就地动态规划
优先清理
实时动态规划
就地(In-Place)动态规划
同步值迭代存储了值函数的两个副本,对于每一个s∈Ss∈S
vnew(s)<−maxa∈A(R(s,a)+γ∑s′∈SPass′vold(s′))vnew(s)<−maxa∈A(R(s,a)+γ∑s′∈SPss′avold(s′))
vold<−vnewvold<−vnew
就地动态规划近存储一个副本,对于每一个s∈Ss∈S
v(s)<−maxa∈A(R(s,a)+γ∑s′∈SPass′v(s′))v(s)<−maxa∈A(R(s,a)+γ∑s′∈SPss′av(s′))
可见就地动态规划,每一次的更新与值遍历的顺序有关系
优先清理 (Prioritised Sweeping)
使用贝尔曼误差的大小来知道状态的选择:
使用贝尔曼误差的大小来知道状态的选择:
|maxa∈A(R(s,a)+γ∑s′∈SPass′v(s′))−v(s)||maxa∈A(R(s,a)+γ∑s′∈SPss′av(s′))−v(s)|
只备份当前贝尔曼误差最大的状态,每次备份之后,更新受到影响的状态的贝尔曼误差,受到影响的状态分两类:
- 更新的状态为s,这种状况贝尔曼误差为0
- 更新的状态为s′s′,要求知道逆运动学(前驱状态)
在编程上,可以通过维护一个优先队列来完成,更新过的状态排到最后面,与实时的不同点是每个状态的更新次数是不同的,继续更新的状态会更多的排到前面,效率比同步的高很多
实时动态规划考虑了时间粒度的操作,只有和智能体相关的状态会被备份,用智能体的经验去指导状态的选择。在每个时间步t上,智能体与环境交互了St,At,Rt+1St,At,Rt+1,备份状态StSt
v(St)<−maxa∈A(R(St,a)+γ∑s′∈SPaSts′v(s′))v(St)<−maxa∈A(R(St,a)+γ∑s′∈SPSts′av(s′))
并不能保证每个状态被遍历,需要结合一定的探索方法,因为有时候环境复杂,需要进行一定程度的探索
全宽备份和样本备份
全宽备份表示对每一次备份都要考虑到每一个后继状态以及每一个动作,要求指导奖励函数R和状态转移函数P。当状态数据较少时,动态规划很有效,反之(维度灾难),每一次备份都会需要很久的时间
强化学习主要使用样本备份,直接通过采样得到转移记录,通过采样替代总体,优点:
强化学习主要使用样本备份,直接通过采样得到转移记录,通过采样替代总体,优点:
- 无模型:无需知道R和P
- 通过采样打破维度灾难
- 备份的时间复杂度固定,和状态的数量无关
判断算法收敛和收敛速度的神器