二叉树实现

二叉树的概念：

n（n≥0）个结点的有限集合，由一个根结点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成。每个根节点只有2个子节点的就叫做二叉树。

1.只有一个根节点
2.根节点只有左子树
3.根节点只有右子树
4.根节点有左子树和右子树

二叉树对应的方法有：

insert(number):插入数据

search(number):搜索对应的数据

min():数据中的最小值

max():数据中的大值

inOrderTraverse():中序遍历所有节点

preOrderTraverse():先序遍历所有节点

postOrderTraverse():后序遍历所有节点

基础数据构建：

class ChildrenTree {
    constructor(data,leftChild,rightChild) {
        this.leftChild = leftChild;
        this.number = data;
        this.rightChild = rightChild
    }
}

构建树：

class tree {
    //data代表当前树
    constructor(num) {
        if(num){
            //创建节点
            this.data = new ChildrenTree(num);
        }else{
            this.data = null;
        }
    }
    //创建节点    insertData(num){
        //创建根节点
        if (!this.data){
            this.data = new ChildrenTree(num);
            return;
        }
        //创建子节点（看后续方法）        insertNode(num,this.data);
    }
    //打印数据节点
    printTree(){
        console.log(JSON.stringify(this.data));
    }
    //搜索对应节点
    search(num){
        if (num === this.data.number){
            return true;
        }
        //搜索对应的方法（看后续方法）

        return searchNode(num,this.data)
    }
    //搜索当前节点最小值
    min(){
        let nums = this.data;
        while (checkData(nums.leftChild)){
            nums = nums.leftChild;
        }
        return nums.number;
    }
    //搜索当前节点最da值    max(){
        let nums = this.data;
        while (checkData(nums.rightChild)){
            nums = nums.rightChild;
        }
        return nums.number;
    }
    //中序遍历
    inOrderTraverse(){
        //中序对应方法（看后续方法）
        console.log(inOrderTraverseNode(this.data));
    }
    //先序遍历
    preOrderTraverse() {
        //先序遍历方法（看后续方法）
        console.log(preOrderTraverseNode(this.data));
    }
    //后序遍历
    postOrderTraverse() {
        //后序遍历方法(看后续方法)
        console.log(postOrderTraverseNode(this.data));
    }

}

对应的方法：

//后序遍历递归方法实现
function postOrderTraverseNode(data) {
    let res = [];
    if (data.leftChild){
        res = res.concat(postOrderTraverseNode(data.leftChild));
    };
    if(data.rightChild){
        let rig = postOrderTraverseNode(data.rightChild);
        res = res.concat(rig);
    }
    res.push(data.number);
    return res;
}
//先序遍历方法递归方法实现
function preOrderTraverseNode(data) {
    let res = [];
    res.push(data.number);
    if (data.leftChild){
        res = res.concat(preOrderTraverseNode(data.leftChild));
    };
    if(data.rightChild){
        let rig = preOrderTraverseNode(data.rightChild);
        res = res.concat(rig);
    }
    return res;
}
//中序遍历方法递归方法实现
function inOrderTraverseNode(data) {
    let res = [];
    if (data.leftChild){
        res = res.concat(inOrderTraverseNode(data.leftChild));
    };
    res.push(data.number);
    if(data.rightChild){
        let rig = inOrderTraverseNode(data.rightChild);
        res = res.concat(rig);
    }
    return res;
}
//检查当前数据是否为空
function checkData(number){
    if (number === undefined || number === null || number === ''){
        return false;
    }
    return true;
}
//递归数据插入
function insertNode(num,current) {
    if (!current){
        current = new ChildrenTree(num);
        return;
    }
    if (num > current.number){
        if (current.rightChild){
            insertNode(num,current.rightChild);
        }else{
            current.rightChild = new ChildrenTree(num);
        }
    }else {
        if (current.leftChild){
            insertNode(num,current.leftChild);
        }else{
            current.leftChild = new ChildrenTree(num);
        }
    }
}
//递归查询当前数据
function searchNode(num,current) {
    if (!current){
        return false;
    }
    if (current.number === num){
        return true;
    }
    if (num > current.number){
        return searchNode(num,current.rightChild);
    }else{
        return searchNode(num,current.leftChild);
    }
}

进行数据测试：

function init() {
    let tree1 = new tree();
    tree1.insertData(11);
    tree1.insertData(13);
    tree1.insertData(7);
    tree1.insertData(5);
    tree1.insertData(8);
    tree1.insertData(1);
    tree1.insertData(2);
    tree1.insertData(18);
    tree1.printTree();
    console.log(tree1.search(11));
    console.log(tree1.search(2));
    console.log(tree1.search(18));
    console.log(tree1.search(17));
    console.log(tree1.min())
    console.log(tree1.max());
    tree1.inOrderTraverse();
    tree1.preOrderTraverse();
    tree1.postOrderTraverse();
}

init();

打印数据结果：

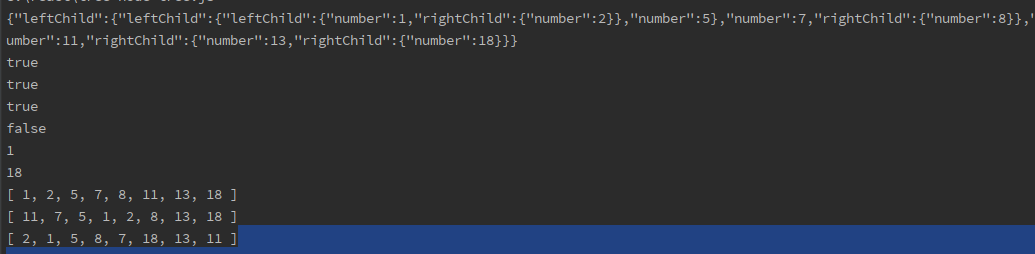
对应生成的树结构：

结果与理论结果一样。