总结

计算机中用二进制来存储小数，大部分小数转成二进制之后都是无限循环的值，因此存在取舍问题，也就是精度丢失。

解决方案：使用 mathjs、使用 tofixed、小数和整数分开相加、与 Math.pow(2,-52) 比较（如下）

function equal(number1, number2) {
return Math.abs(number1 - number2) < Math.pow(2, -52);
}
console.log(equal(0.1 + 0.2, 0.3));

既定事实

在 js 中能否表示的数字的绝对值范围是 5e-324 ~ 1.7976931348623157e+308，这一点可以通过 Number.MAX_VALUE 和 Number.MIN_VALUE 来得到证实
在 js 中能够表示的最大安全整数的范围是：-9007199254740991 ~ 9007199254740991，可以通过 Number.MIN_SAFE_INTEGER 和 Number.MAX_SAFE_INTEGER 来求证

存在问题

在四则运算中存在精度丢失的问题

0.1 + 0.2 //0.30000000000000004

超过最大安全整数的运算是不安全的，

9007199254740991 + 2 // 9007199254740992

原因

JS 中的 number 类型使用的是双精度浮点型，也就是其他语言中的 double 类型
双精度浮点数使用 64 bit 来进行存储

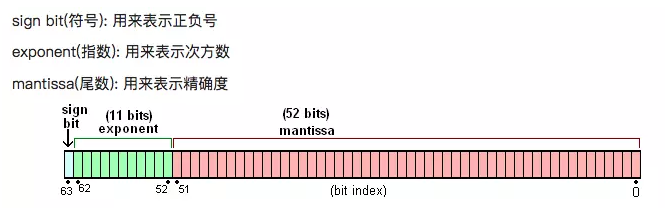
Number 在内存中会被表示成：

s x m x 2^e

Es 规范中规定 e 的范围在 -1074~971，m 能表示的最大数是 52个1，最小能表示的是1 二进制的第一位有效数字必定是1，因此这个1不会被存储，可以节省一个存储位，因此尾数部分可以存储的范围是1 ~ 2^(52+1) 也就是说 Number 能表示的最大数字绝对值范围是 2^-1074 ~ 2^(53+971)

精度丢失

0.1 和 0.2 转换成二进制的结果：

(0.1)10 => (00011001100110011001(1001)...)2
(0.2)10 => (00110011001100110011(0011)...)2

0.1 和 0.2 转成二进制之后都是一个无限循环的数，53位有效数字只能进行四舍五入最后得到的结果就是 0.30000000000000004

JS 数据类型：0.1+0.2=?

总结

既定事实

存在问题

原因

精度丢失