最近把吃灰很久的<算法导论>拿出来翻了一下，发现经典不亏是经典。

对于树类的数据结构，一直掌握的不够透彻，本文作为自己的一个学习总结，方便以后查阅。

B树

首先对B树有一个初步的认识：

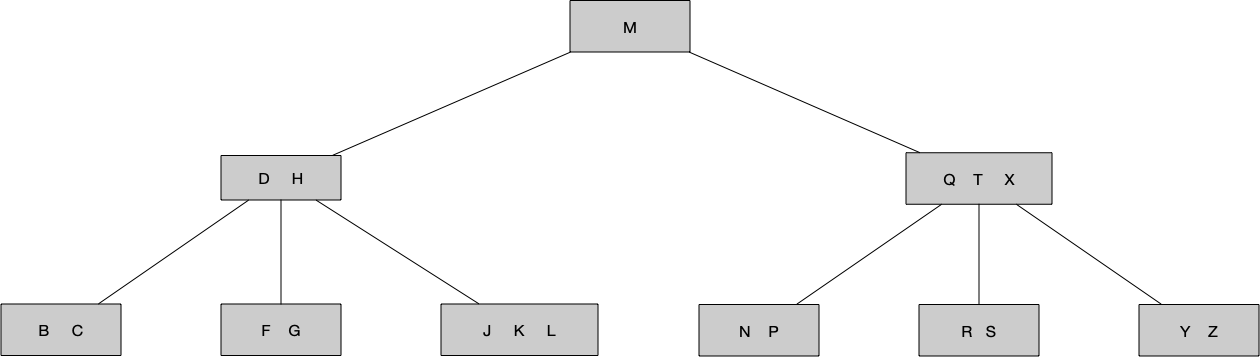
如果B树的一个内部节点X包含有X.n个关键字，那么节点X就有X.n+1个孩子。

在B树中，关键字做为分隔点，把当前节点所处理的关键字分隔为X.n+1个子域，每个子域都由其的一个孩子表示。

定义

一颗B树T是具有以下性质的有根树(T.root)

对于每个节点X，具有以下属性：

X.n表示当前储存在节点X中的关键字个数。
X.n个关键字本身，记为X.key₁,X.key₂,...X.key_n。以升序排列。
X.leaf，布尔值，用来记录当前节点X是否为叶子节点。
每个内部节点X包含有X.n+1个指向其孩子节点的指针，记为X.c₁,X.c₂,...X.c_n+1。其中叶子节点没有孩子。
关键字X.key_i对存储在各子树中的关键字范围加以分隔。如果K_i为任一一个存储在以X.c_i为根的子树中的关键字，那么： K₁<=X.key₁<=K₂<=X.key₂<=...<=X.key_X.n<=K_Xn+1
每个叶子节点具有相同的深度，记为h。
每个节点所包含的关键字个数有上界下界。被称为B树的最小度数，记为t(t>=2)。
除了根节点外，每个节点至少有t-1个关键字。
每个节点最多包含2t-1个关键字。如果一个节点恰好有2t-1个关键字时，称该节点是满的。

可以将B树理解为二叉树的一种扩展 -> 由二叉树的两路扩展成了多路。

简单来说，B树中一个节点应该是下面这个样子：

在一个节点中，我们用两个数组分别来储存当前节点的关键字信息key[]和孩子指针c[]，其结构如下图所示（未画叶子节点中数据）：

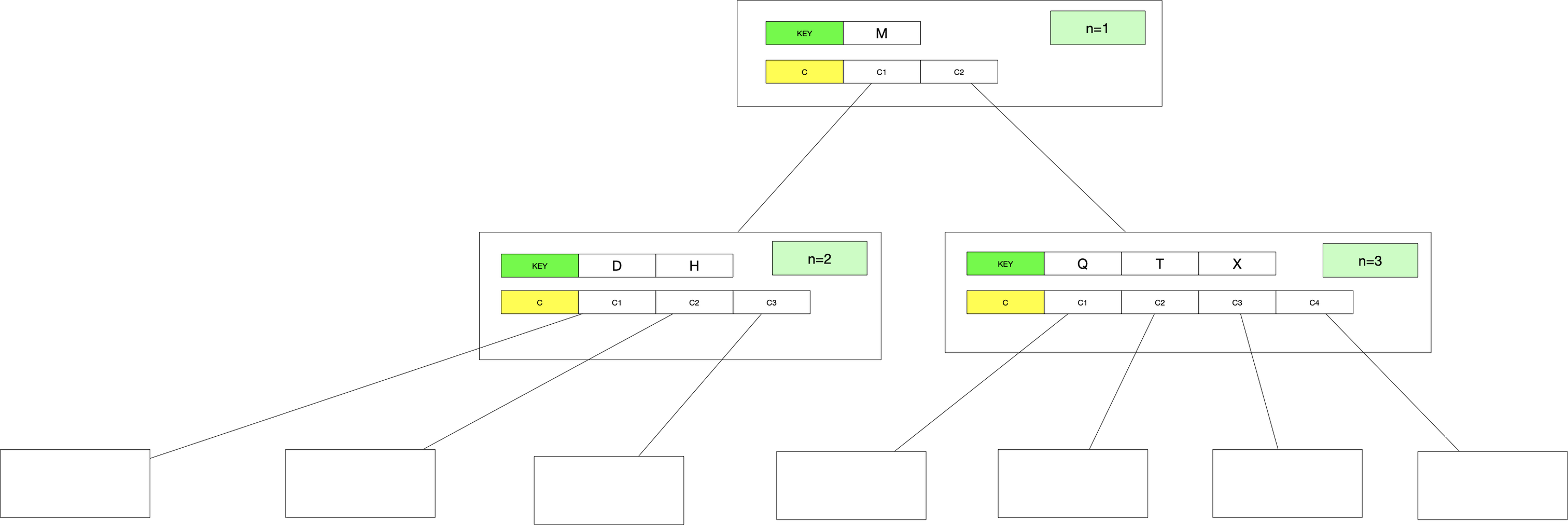
其中C为当前节点的孩子指针数组。根据B树的定义，当前树最小度数t=2，叶子节点深度h=3。

B树中的基本操作

搜索🌲

B树在结构上与二叉树很类似，只不过B树中节点的孩子个数可能>2，所以，在根据节点做分支选择时做的是n+1路选择。下图画出了从根节点出发，在B树中查找关键字G的过程：

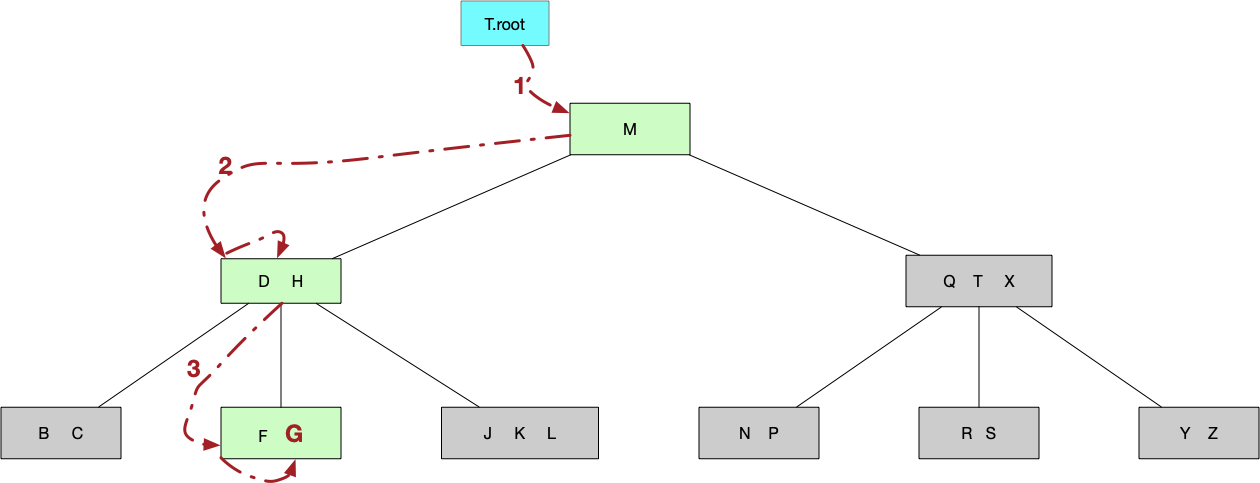
从根节点M出发，发现目标字母G比节点M小，说明目标位于子树1中。
到节点D H，由于目标字母G大于D，且小于H,说明目标位于子树2中。
到节点F G，找到目标字母G。

搜索过程比较简单，与二叉树类似，这里直接给出伪代码。

查找以X为根节点的B树种中关键字k的位置：

B-TREE-SEARCH(X,k){
    i=i
    while i<=X.n and k>X.key[i]     //在当前节点中找出关键字 <= 目标k的最小下标
        i = i+1
    if i<= X.n and k == X.key[i]    //目标k是否存在于当前节点中      
        return (X,i)
    else if X.leaf                  //不在当前节点中，且当前节点为叶子节点
        return null
    else 
        return B-TREE-SEARCH(X.c[i],k) //递归查找子树
}

插入🌲

B树中插入一个关键字要比二叉树插入一个关键字复杂。

与二叉树相同的是，在插入时需要查找插入新关键字的叶节点位置。然而在B树种，不能简单地创建一个新的叶节点，然后将其插入。因为这样得到的树将不会是一个合法的B树。相反的是，我们需要将关键字插入到一个已有的叶节点上。

分裂

由于不能将关键字插入一个满的叶节点，所以引入一个分裂操作：

将一个满的节点(2t-1个关键字)按其中间关键字分裂为两个个t-1个关键字组成的节点。中间关键字上升成为他们的父节点。

如果父节点由于子节点的分裂变为了满节点，则该分裂过程需要向上传播，直到遇到非满的节点。
在分裂向上传播的过程中，如果传播至根节点，且根节点变为满节点后，同样需要将根节点进行分裂，使树长高。

为了应对分裂向上传播,我们做出这样的优化：

并不是等到找出插入过程中实际要分裂的满节点时才做分裂。相反，我们将从根节点开始，将沿树向下查找关键字位置时就将所经过的所有满节点进行分裂操作。

下图描述了一个节点的分裂过程：

结合图来看，分裂一个关键字节点可以分为三步：

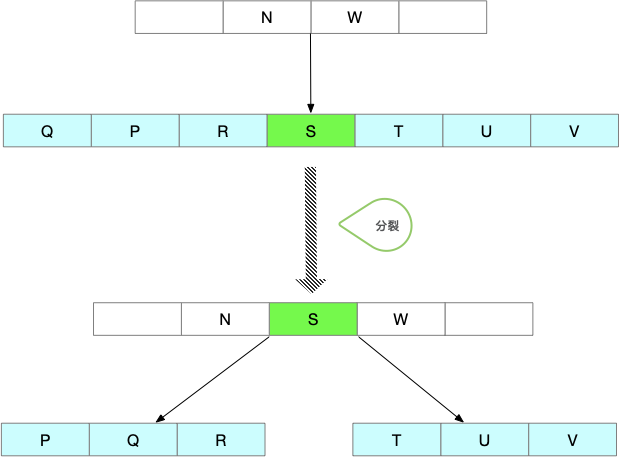
创建一个新的节点，并将位于S后的关键字赋给新节点（包含关键字和孩子节点）。
调整将要分裂节点的关键字信息，使其只含有关键字S前的关键字。
将父节点中W及其之后元素后移一位，同时将关键字S上提，使其分隔原本的节点。

下面举例说明：

分裂前数据状态，节点Y位于节点N,M之间，X节点中C2储存子节点Y的指针：

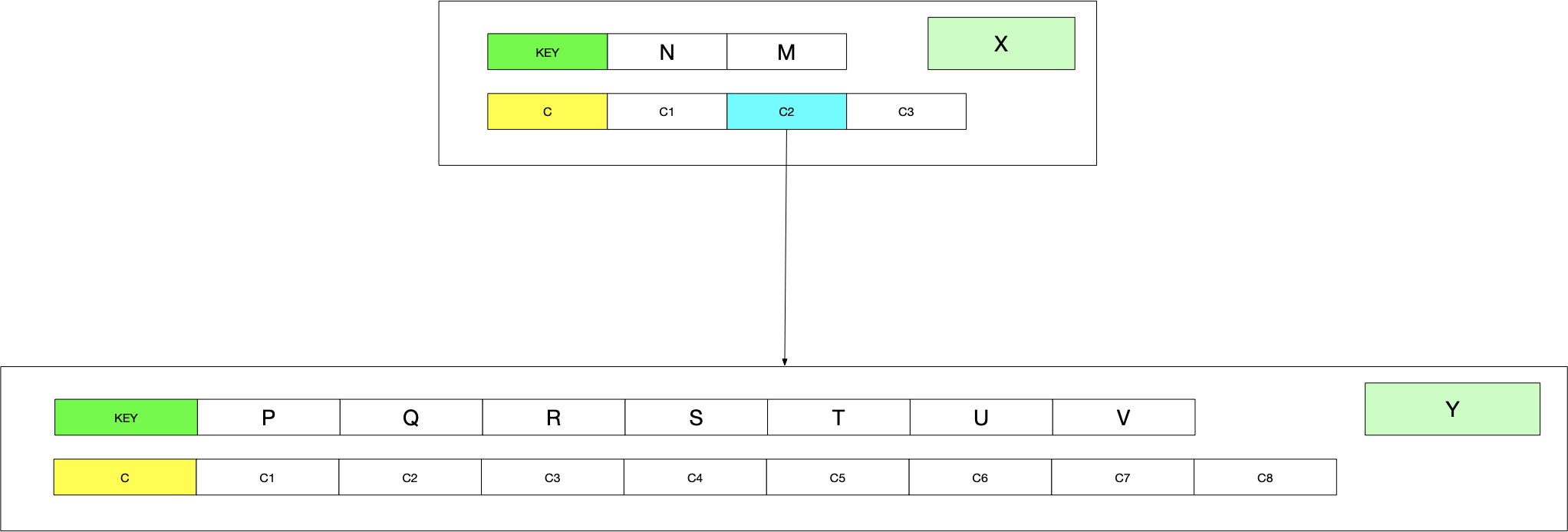
创建新的节点Z，并赋值：

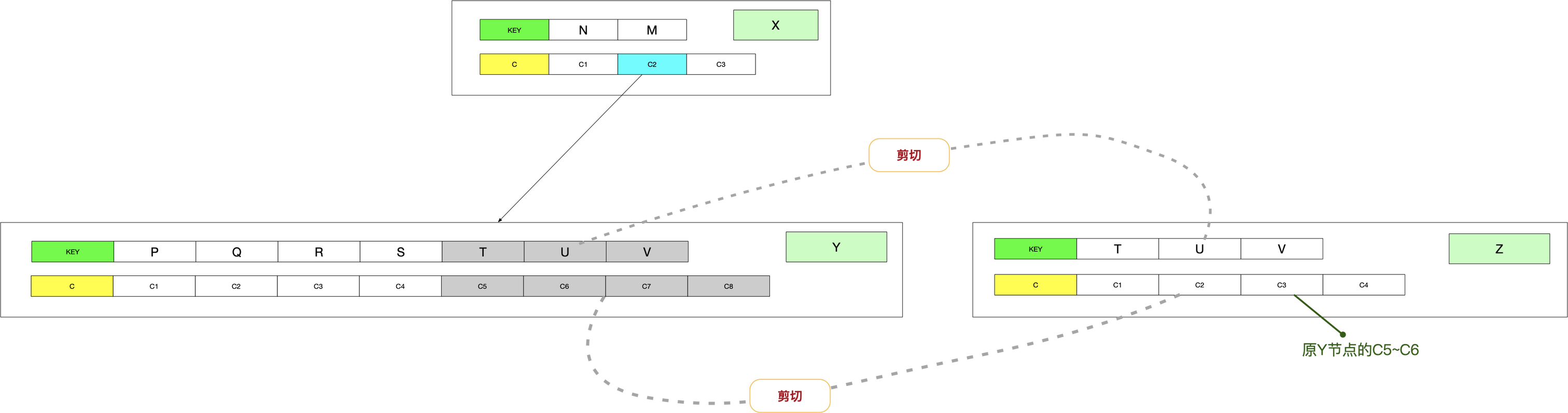
这里使用剪切的方式，将原Y节点中的后3个关键字和后4个孩子指针移入新节点Z中。

将X节点关键字和孩子节点指针后移，将S节点插入,并将原X节点的C3后移成为C4，插入新的C3指向Z节点：

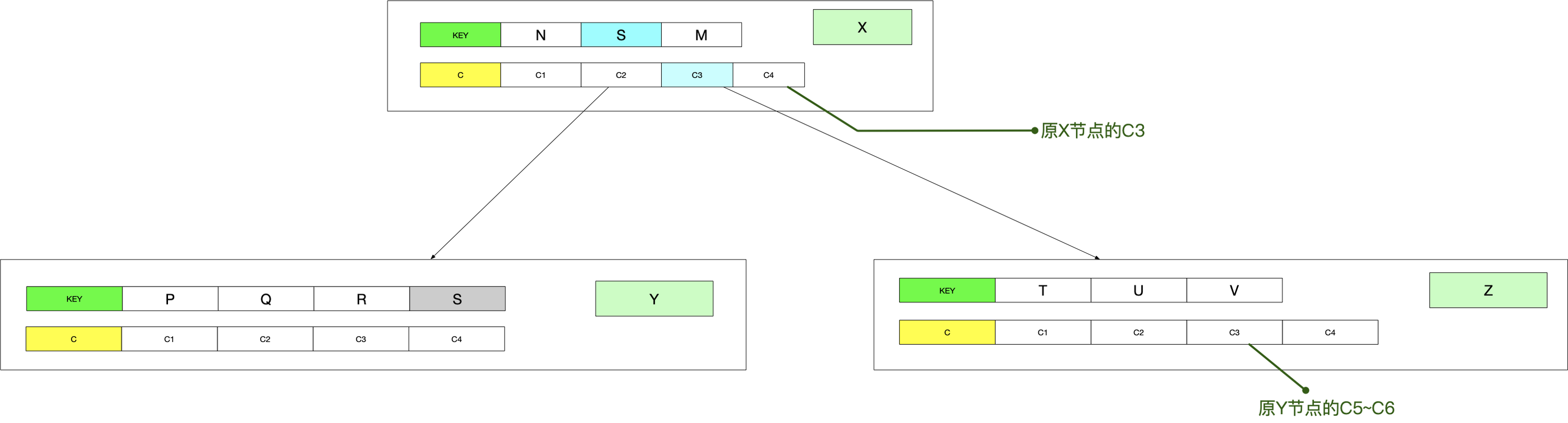
一句话总结一下：分裂即是将一个满的节点(2t-1个关键字)按其中间关键字key[t]分裂为两个各含t-1个关键字的节点，并将中间关键字提升至父节点。

下面为分裂的伪代码：

B-TREE-SPLIT-CHILD(x,i)                 //x为非满节点，i为使x.c[i]节点为x的满子节点的下标
                                        //在上面的例子中，入参x即为节点X，i为X.C2的下标2
    z = new Node()                      //.......创建z节点.........
    y = x.c[i]
    z.leaf = y.leaf                     //因为z是从y分裂出来的，所以leaf是一样的
    z.n = t-1                           //分裂出的每个子节点度都为t-1
    for j = 1 to t-1                    //赋值关键字
        z.key[j] = y.key[j+t]
    if not y.leaf                       //如果不是叶子节点，需要赋值孩子指针
        for j = 1 to t
            z.c[j] = y.c[j+t]           //.......以上是创建Z节点........
    y.n = t-1
    for j = x.n+1 downto i+1            //将父节点x中的孩子指针后移一位
        x.c[j+1] = x.c[j]
    x.c[i+1] = z
    for j = x.n downto i                //将父节点x中的关键字后移一位
        x.key[j+1] = x.key[j]
    x.key[i] = y.key[t]                 //中间关键字上提至父节点
    x.n = x.n + 1

插入

目前我们已经有了将满节点分裂的能力，所以可以容易的写出插入关键字的伪代码：

B-TREE-INSERT可以利用上面的分裂子程序来保证递归始终不会落到一个满节点上。

B-TREE-INSERT(T,k)
    r = T.root
    if r.n == 2t-1                          //如果当前为满节点
        s = new Node()
        T.root = s
        s.leaf = FALSE
        s.n = 0
        s.c[1] = r
        B-TREE-SPLIT-CHILD(s,1)             //将原有的根节点分裂         
        B-TREE-INSERT-NONFULL(s,k)
    else
        B-TREE-INSERT-NONFULL(r,k)

在伪代码B-TREE-INSERT中，如果当前树度t=3，有一个节点X为满节点。

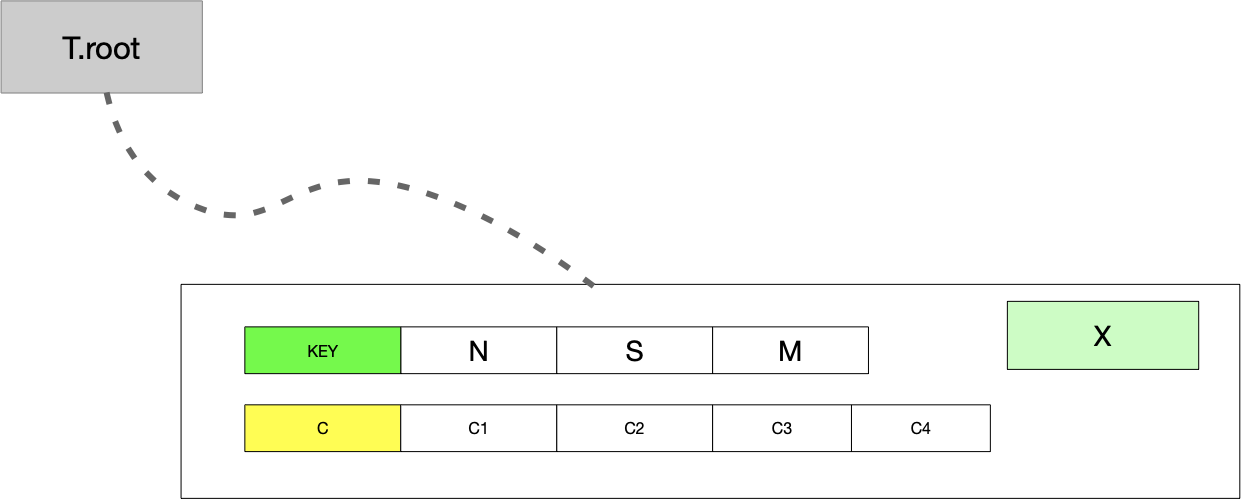
因为我们的插入过程需要从根节点开始，将沿树向下查找关键字位置时将所经过的所有满节点进行分裂操作，所以，在经过该节点X时，需要将他分裂。

下图为准备分裂的过程，创建节点S，可以在伪代码或图中看到，他是一个空节点：

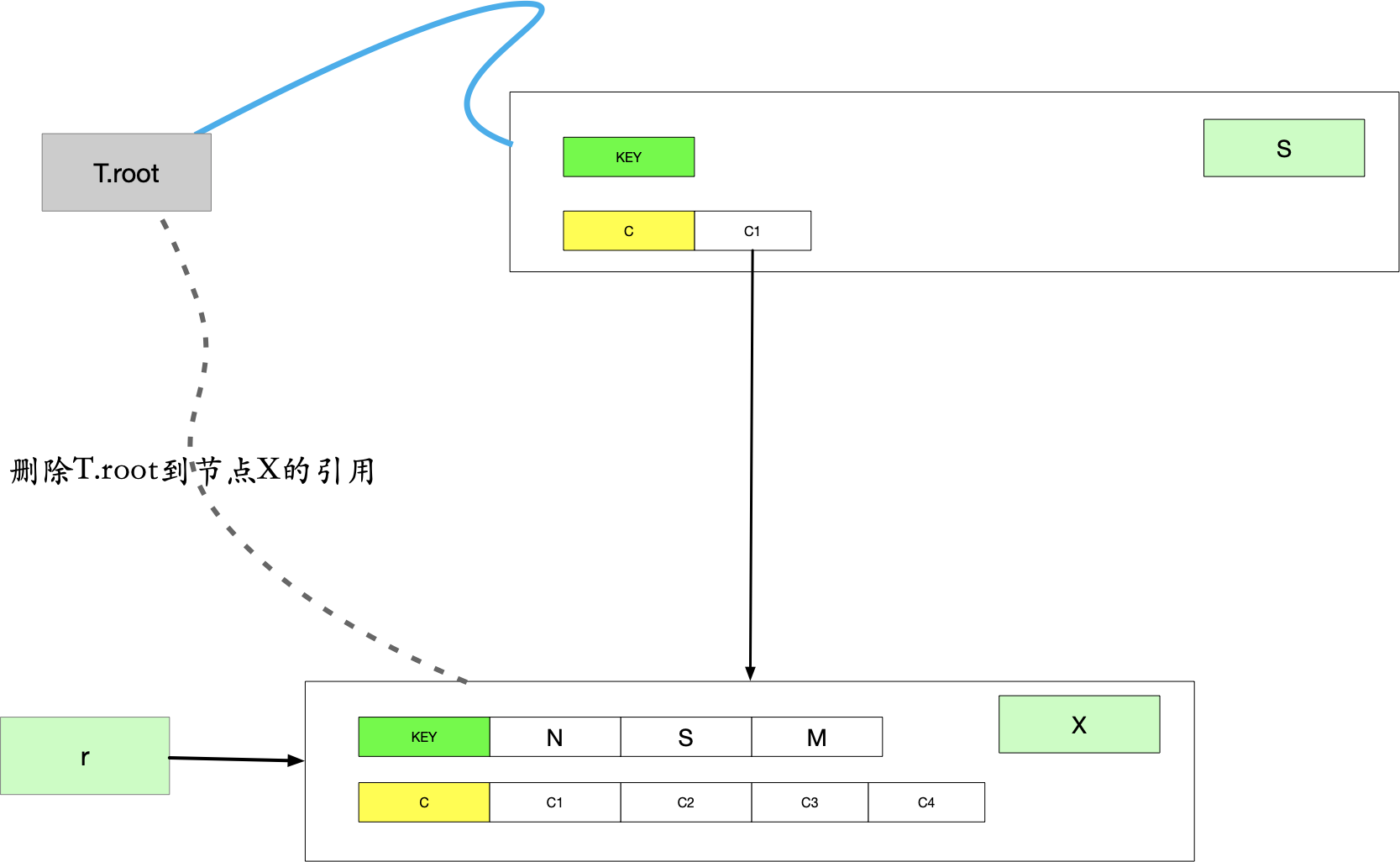
以S为根节点，1为孩子节点下标进行分裂，由于对S节点的孩子C1进行了分裂：会将X的中间关键字上提至S节点。

这里直接给出分裂后的结果：

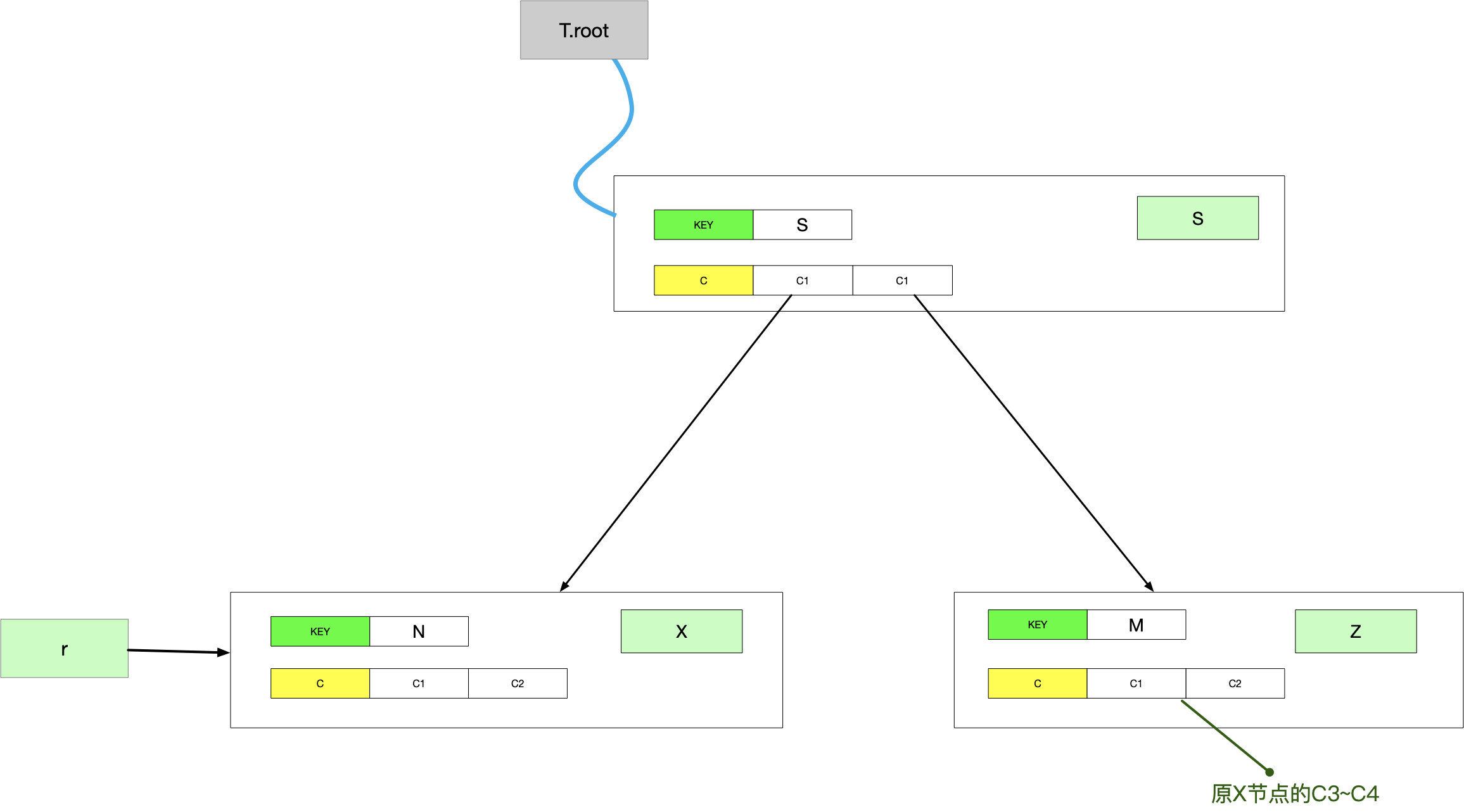
到目前为止，我们已经有能力保证发生插入的节点一定是非满节点。所以，可以假设调用过程B-TREE-INSERT-NONFULL时X节点是非满的：

B-TREE-INSERT-NONFULL(x,k)
    i = x.n
    if x.leaf                           //-------叶子节点--------
        while i >= i and k < x.key[i]
            x.key[i+1] = x.key[i]
            i--
        x.key[i+1] = k                  // 将元素后移后 插入关键字k
        x.n = x.n + 1                   //----end 叶子节点-------
    else                                
        while i >= 1 and k < x.key[i]   //------非叶子节点-------
            i--
        i++
        if x.c[i].n == 2t-1             //如果子节点为满节点
            B-TREE-SPLIT-CHILD(x,i)
            if k > x.key[i]             //因为上面将X节点做了分裂，
                i++                     //  所以这里需要判断将下沉到那个子节点上
        B-TREE-INSERT-NONFULL(x.c[i],k)//插入k到子节点(递归)

可以看出，过程B-TREE-INSERT-NONFULL只是简单的插入关键字到叶子节点。

至此，B树的插入，查找过程已经全部解析完成。

B树的删除过程比插入略微复杂一些，将在后面分析。

参考资料

《算法导论》

高级数据结构--B树

B树

定义

B树中的基本操作

搜索🌲

插入🌲

分裂

插入

参考资料