股票交易
股票问题一开始是想用递归解决的,但是递归实在没想到怎么做,就去题解区看大佬的解法,然后看到了状态机的解法,惊为天人,现在做一下总结。
- dp[i][k][1]:第i天,持有股票,还剩下k次交易机会
- dp[i][k][0]:第i天,未持有股票,还剩下k次交易机会
状态转移方程
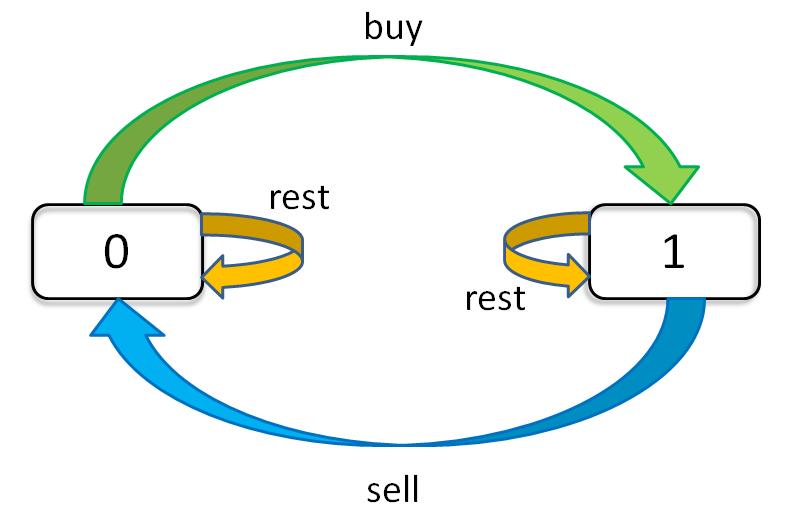
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
max( 选择 rest , 选择 sell )
解释:今天我没有持有股票,有两种可能:
要么是我昨天就没有持有,然后今天选择 rest,所以我今天还是没有持有;
要么是我昨天持有股票,但是今天我 sell 了,所以我今天没有持有股票了。
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
max( 选择 rest , 选择 buy )
解释:今天我持有着股票,有两种可能:
要么我昨天就持有着股票,然后今天选择 rest,所以我今天还持有着股票;
要么我昨天本没有持有,但今天我选择 buy,所以今天我就持有股票了。
base case
dp[-1][k][0] = dp[i][0][0] = 0
dp[-1][k][1] = dp[i][0][1] = -infinity
具体的应用看接下来的解答
309. 最佳买卖股票时机含冷冻期(Medium)
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票): 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
示例:
输入: [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
题解:应用上面所讲的方法,可以得出转移方程:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
解释:第 i 天选择 buy 的时候,要从 i-2 的状态转移,而不是 i-1 。
不限制交易次数的话,k就可以省略
class Solution {
public int maxProfit(int[] prices) {
if(prices.length == 0 || prices == null){
return 0;
}
int n = prices.length;
//定义dp数组并初始化
int dp[][] = new int[n][2];
for (int i = 0; i < prices.length; i++) {
if (i == 0){
//第0天没持有股票利润是0
dp[0][0] = 0;
//持有了就为价格的负数
dp[0][1] = -prices[i];
continue;
}else if (i == 1){
dp[1][0] = Math.max(dp[0][0], dp[0][1] + prices[i]);
dp[1][1] = Math.max(dp[0][1], dp[0][0] - prices[i]);
continue;
}
//当天有两种状态:持有/未持有股票
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
//卖出之后隔一天才能买,所以i=1要单独写
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][0] - prices[i]);
}
return dp[n - 1][0];
}
}
714. 买卖股票的最佳时机含手续费(Medium)
给定一个整数数组 prices,其中第 i 个元素代表了第 i 天的股票价格 ;非负整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每次交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。返回获得利润的最大值。
示例 1:
输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
解释: 能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
注意:
0 < prices.length <= 50000.
0 < prices[i] < 50000.
0 <= fee < 50000.
解析:这道题上道题很类似,转移方程大体一致,不同的是这道题交易需要手续费,买入卖出算一次手续费,而且相较于上道题,这道题脉脉股票没有冻结期,所以转移方程如下
- dp[i][0]=Math.max(dp[i-1][0], dp[i-1][1]+prices[i]-fee)
- dp[i][1]=Math.max(dp[i-1][1], dp[i-1][0]-prices[i])
class Solution {
public int maxProfit(int[] prices, int fee) {
if (prices == null || prices.length == 0){
return 0;
}
int n = prices.length;
//可任意交易n次,所以交易次数可以不考虑
int[][] dp = new int[n][2];
for (int i = 0; i < n; i++) {
if (i == 0){
dp[0][0] = 0;
dp[0][1] = -prices[i];
}else {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
}
return dp[n - 1][0];
}
}
123. 买卖股票的最佳时机 III(Hard)
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。 注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [3,3,5,0,0,3,1,4]
输出: 6
解释: 在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。 随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这个情况下, 没有交易完成, 所以最大利润为 0。
题解:
- 这道题乍一看跟前面两道题区别不大,只是交易次数有无数次变为了两次,没有手续费而已,但是回去看一下最开始的转移方程,便可以发现前面两道题的解法是跟k关系不大的,但是这道题由于k=2,所以k便不能够省略。
- 按照前面总结的“穷举框架”,我们需要穷举出所有的状态,如果按照一开始的方法写(如下),便会出错,因为我们没有对k进行穷举,所以需要做的是加上对k的穷举
错误的:
int k = 2;
int[][][] dp = new int[n][k + 1][2];
for (int i = 0; i < n; i++)
if (i - 1 == -1) { /* 处理一下 base case*/ }
dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
return dp[n - 1][k][0];
正确的:
int max_k = 2;
int[][][] dp = new int[n][max_k + 1][2];
for (int i = 0; i < n; i++) {
for (int k = max_k; k >= 1; k--) {
if (i - 1 == -1) {
/* 处理 base case */
dp[i][k][0] = 0;
dp[i][k][1] = -prices[i];
continue;
}
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
}
// 穷举了 n × max_k × 2 个状态,正确。
return dp[n - 1][max_k][0];
解答:
class Solution {
public int maxProfit(int[] prices) {
if (prices == null || prices.length == 0){
return 0;
}
int maxk = 2;
int n = prices.length;
int[][][] dp = new int[n][maxk + 1][2];
for (int i = 0; i < n; i++) {
//不能任意交易n次,所以交易次数需要考虑,交易次数最小为1
for (int k = 1; k <= maxk; k++) {
if (i == 0){
dp[0][k][0] = 0;
dp[0][k][1] = -prices[i];
}else {
dp[i][k][0] = Math.max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i]);
//买入股票的时候,交易次数就减一
dp[i][k][1] = Math.max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i]);
}
}
}
return dp[n - 1][maxk][0];
}
}
188. 买卖股票的最佳时机 IV(Hard)
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。 注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。 随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
题解:这道题和上道题的解法基本一致,不同点在于上道题是只能交易2次,这道题可以交易k次,但是k是有限的,按照上道题的方法进行解答会出现超出内存的错误,原因是如果k过大,那么初始化的数组会很大,就容易超出内存,仔细分析,买卖一只股票需要两天,所以大小为n的prices数组最多可以进行n/2次交易,如果k超出这个限制,那么k就没有意义了,此次就转为第一道题的解法了。
class Solution {
public int maxProfit(int[] prices, int maxk) {
if (prices == null || prices.length == 0) {
return 0;
}
int n = prices.length;
//k超出n的一半,则k无意义
if (maxk > n / 2) {
return maxProfit(prices);
}
int[][][] dp = new int[n][maxk + 1][2];
for (int i = 0; i < n; i++) {
//不能任意交易n次,所以交易次数需要考虑
for (int k = 1; k <= maxk; k++) {
if (i == 0) {
dp[0][k][0] = 0;
dp[0][k][1] = -prices[i];
} else {
dp[i][k][0] = Math.max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i]);
//买入股票的时候,交易次数就减一
dp[i][k][1] = Math.max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i]);
}
}
}
return dp[n - 1][maxk][0];
}
private int maxProfit(int[] prices) {
if (prices.length == 0 || prices == null) {
return 0;
}
int n = prices.length;
//定义dp数组并初始化
int dp[][] = new int[n][2];
for (int i = 0; i < prices.length; i++) {
if (i == 0) {
//第0天没持有股票利润是0
dp[0][0] = 0;
//持有了就为价格的负数
dp[0][1] = -prices[i];
continue;
} else if (i == 1) {
dp[1][0] = Math.max(dp[0][0], dp[0][1] + prices[i]);
dp[1][1] = Math.max(dp[0][1], dp[0][0] - prices[i]);
continue;
}
//当天有两种状态:持有/未持有股票
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
//卖出之后隔一天才能买,所以i=1要单独写
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][0] - prices[i]);
}
return dp[n - 1][0];
}
}
字符串编辑
583. 两个字符串的删除操作(Medium)
给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。
示例 1:
输入: "sea", "eat"
输出: 2
解释: 第一步将"sea"变为"ea",第二步将"eat"变为"ea"
说明:
给定单词的长度不超过500。
给定单词中的字符只含有小写字母。
暴力递归解法:这道题的关键是要能够想到:要求使得两个字符串相等的最小步数,可以转换为求两字符串相等的最大长度,对于长度分别为len1和len2的字符串:
- 如果它们的最后一个字符相等,那么它们的最长公共子串可以表示为:lcs(len1, len2)=lcs(len1-1,len2-1)+1
- 如果最后一个字符不想等,例如,"abcd"和"abc",这时的最长公共子串长度可表述为:lcs(len1, len2)=Math.max(lcs(len1-1,len2),lcs(len1,len2-1))
- 为了避免大量重复的计算,引入记忆数组
class Solution {
private int[][] memo;
public int minDistance(String word1, String word2) {
if (word1 == null || word2 == null){
return 0;
}
int len1 = word1.length();
int len2 = word2.length();
memo = new int[len1][len2];
for (int i = 0; i < memo.length; i++) {
for (int j = 0; j < memo[0].length; j++) {
memo[i][j] = -1;
}
}
int result = minDistance(word1, word2, len1 - 1, len2 - 1);
return result;
}
private int minDistance(String word1, String word2, int i, int j) {
//base case:任何一个字符串到达最后,递归结束
if (i == -1 || j == -1){
return 0;
}
//如果已经出现过,直接返回
if (memo[i][j] != -1){
return memo[i][j];
}
int res;
//最后一个字符相等
if (word1.charAt(i) == word2.charAt(j)){
res = minDistance(word1, word2, i - 1, j - 1) + 1;
}else {
//不想等
res = Math.max(minDistance(word1, word2, i - 1, j), minDistance(word1, word2, i, j - 1));
}
memo[i][j] = res;
return res;
}
}
解法二:转为动态规划,老方法。
public class Solution {
public int minDistance(String word1, String word2) {
if (word1 == null || word2 == null){
return 0;
}
int len1 = word1.length();
int len2 = word2.length();
//dp[i][j]表示word1前i个字符和word2前j个字符的最大公共字符数
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1] + 1;
}else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return len1 + len2 - 2 * dp[len1][len2];
}
}
72. 编辑距离(Hard)
给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例 1:
输入: word1 = "horse", word2 = "ros"
输出: 3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:
输入: word1 = "intention", word2 = "execution"
输出: 5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
解法一:参考labuladong大佬的解法,解决两个字符串的动态规划问题,一般都是用两个指针i,j指向两个字符串的末尾,然后一步步往前,缩小问题的规模。
设两个字符串分别为 "rad" 和 "apple",为了把 s1 变成 s2,算法会这样进行(借鉴大佬的图):

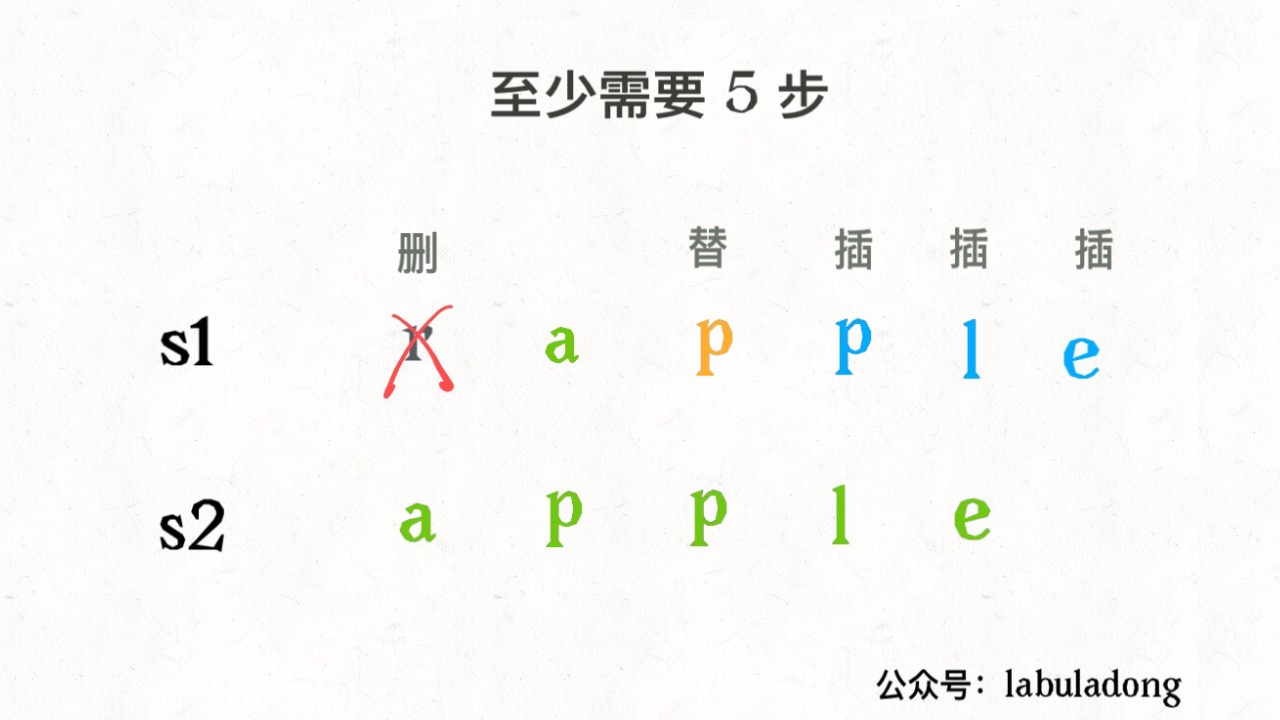
如果算上两个字符相等就跳过的情况,那么一共4种操作。
base case:
- 当i先走完全程的时候,就用插入操作把s2剩下的字符插入到s1
- 反之j先走完,那么只能用删除操作把 s1 缩短为 s2。
这种四种情况的递归,往上抽象的话,可以抽象成四叉树的递归。
class Solution {
public int minDistance(String word1, String word2) {
//递归函数的定义:返回s1[0..i] 和 s2[0..j] 的最小编辑距离,
//理解了定义之后,下面的代码会很容易理解
return minDistance(word1, word2, word1.length() - 1, word2.length() - 1);
}
private int minDistance(String word1, String word2, int i, int j) {
//base case:当s1的指针i一先遍历完,直接返回s2剩下的长度
if (i == -1){
return j + 1;
}
if (j == -1){
return i + 1;
}
//如果i和j所表示的字符相等,同时往前移,不需要操作
if (word1.charAt(i) == word2.charAt(j)){
return minDistance(word1, word2, i - 1, j - 1);
}else {
//如果不等的话分别进行三种操作,返回最小的那个
return Math.min(
//删除
minDistance(word1, word2, i - 1, j) + 1,
Math.min(
//添加
minDistance(word1, word2, i, j - 1) + 1,
//替换
minDistance(word1, word2, i - 1, j - 1) + 1));
}
}
}
解法二:暴力递归存在大量重复计算的情况,可以使用“记忆数组”的方式来记录中间已经遍历过的情况
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
int[][] memo = new int[len1 + 1][len2 + 1];
for (int i = 0; i < len1; i++) {
for (int j = 0; j < len2; j++) {
memo[i][j] = -1;
}
}
return minDistance(word1, word2, len1 - 1, len2 - 1, memo);
}
private int minDistance(String word1, String word2, int i, int j, int[][] memo) {
//base case:当s1的指针i一先遍历完,直接返回s2剩下的长度
if (i == -1){
return j + 1;
}
if (j == -1){
return i + 1;
}
//如果已经遍历过,那么直接返回
if (memo[i][j] != -1){
return memo[i][j];
}
//如果i和j所表示的字符相等,同时往前移,不需要操作
if (word1.charAt(i) == word2.charAt(j)){
memo[i][j] = minDistance(word1, word2, i - 1, j - 1, memo);
return memo[i][j];
}else {
//如果不等的话分别进行三种操作,返回最小的那个
memo[i][j] = Math.min(
//删除
minDistance(word1, word2, i - 1, j, memo) + 1,
Math.min(
//添加
minDistance(word1, word2, i, j - 1, memo) + 1,
//替换
minDistance(word1, word2, i - 1, j - 1, memo) + 1));
return memo[i][j];
}
}
}
解法三:老方法,将带记忆数组的递归转为动态规划,不多说了,这两个其实没啥很大区别,时间复杂度也很接近,不过要注意的是动态规划是自底向上的,所以需要初始化
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
//dp[][]的定义:s1[0..i] 和 s2[0..j] 的最小编辑距离
int[][] dp = new int[len1 + 1][len2 + 1];
//初始化dp数组,第一行dp[0][j]代表s1为空时转为s2的最少步骤,自然是等于j;
for (int j = 0; j <= len2; j++) {
dp[0][j] = j;
}
//初始化第一列,跟第一行一样
for (int i = 0; i < len1; i++) {
dp[i][0] = i;
}
//遍历dp数组,根据转移方程填充dp数组
for (int i = 0; i <= len1; i++) {
for (int j = 0; j <= len2; j++) {
//相等的话不用进行操作,直接跳过
if (word1.charAt(i) == word2.charAt(j)){
dp[i][j] = dp[i - 1][j - 1];
}else {
//如果不等的话分别进行三种操作,取最小的那个
dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
}
}
}
return dp[len1][len2];
}
}
650. 只有两个键的键盘(Medium)
最初在一个记事本上只有一个字符 'A'。你每次可以对这个记事本进行两种操作:
- Copy All (复制全部) : 你可以复制这个记事本中的所有字符(部分的复制是不允许的)。
- Paste (粘贴) : 你可以粘贴你上一次复制的字符。
给定一个数字 n 。你需要使用最少的操作次数,在记事本中打印出恰好 n 个 'A'。输出能够打印出 n 个 'A' 的最少操作次数。
示例 1:
输入: 3
输出: 3
解释:
最初, 我们只有一个字符 'A'。
第 1 步, 我们使用 Copy All 操作。
第 2 步, 我们使用 Paste 操作来获得 'AA'。
第 3 步, 我们使用 Paste 操作来获得 'AAA'。
说明:
n 的取值范围是 [1, 1000] 。
解法一:这道题的话给了两个操作,复制当前全部内容和粘贴上次复制的内容。
- 所以给定“n”,最差的情况是复制1次,粘贴n-1次,一共n个步骤
- 还可以先组成n的因数,比如n=6,先将A的数量弄到2或者3,然后复制,继续粘贴,这样也是一种办法 两种情况都列举出来了,就可以按照这个办法进行递归
class Solution {
public int minSteps(int n) {
//base case:初始值为1,所以不用操作
if (n == 1){
return 0;
}
//最多需要n步
int res = n;
//寻找n的因子
for (int i = n - 1; i > 1; i--) {
//如果i是n的因子,那么这个因子可以当做模块的个数,再算出模块长度n/i
//i * n / i = 1
if (n % i == 0){
res = Math.min(res, minSteps(n / i) + i);
}
}
return res;
}
}
解法二:转为动态规划
class Solution {
public int minSteps(int n) {
int[] dp = new int[n + 1];
//初始化dp数组
dp[1] = 0;
//寻找n的因子
for (int i = 2; i <= n; i++) {
//最多需要i步
dp[i] = i;
//如果i是n的因子,那么这个因子可以当做模块的个数,再算出模块长度n/i
//i * n / i = 1
for (int j = i - 1; j > 1; --j) {
if (i % j == 0) {
dp[i] = Math.min(dp[i], dp[j] + i / j);
break;
}
}
}
return dp[n];
}
}
至此,题目多的8行的动态规划也就告一段落了,开始下一征程。